4.4: Velocities and Areas of Sectors

Suggested Prerequisite Topics

This section is designed assuming you understand the following topics from Algebra.

• Distance, rate, and time problems
• Velocity

Learning Objectives

• Calculate the area of a sector formed by a central angle.
• Solve an application involving sector area.
• Calculate the linear velocity of a point moving with uniform circular motion.
• Calculate the angular velocity of a point moving with uniform circular motion.
• Convert from linear velocity to angular velocity and vice versa.
• Solve application problems involving linear and angular velocity.

Areas of Sectors

Now that we have paired angles with real numbers via radian measure, a world of applications awaits us.

We recently discovered the relationship between the length, \( s \), of the arc subtended by an angle \( \theta \) (in radians) in a circle of radius \( r \) to be\[ s = r \theta. \nonumber \]We now investigate the area of the sector formed by this central angle \( \theta \).

Figure \( \PageIndex{ 1 } \): The area of a sector of a circle of radius \( r \) subtended by the angle \( \theta \)

A sector of a circle subtended by a central angle \( \theta \) is the region bounded by the initial and terminal sides of \( \theta \) and the edge of the circle (as shown in Figure \( \PageIndex{ 1 } \)). To find this area, we recall that the total area of a circle of radius \( r \) is \( \pi r^2 \); however, the shaded region in Figure \( 1 \) is not the entire circle. In fact, it is a specific portion of this circle. In terms of angular measure, we have only shaded the region covered by an angle rotated through \( \theta \) out of \( 2\pi \) radians of a full circle. That is, the portion of the circle we have shaded is\[ A = \dfrac{\theta}{2\pi} \, \text{of the area of the full circle} = \dfrac{\theta}{2 \cancel{\pi}} \cdot \cancel{\pi} r^2 = \dfrac{1}{2} r^2 \theta. \nonumber \]This proves the following theorem.

Theorem: Area of a Sector

If \( \theta \) (in radians) is the central angle in a circle of radius \( r \), then the area of the sector subtended by \( \theta \) is\[ A = \dfrac{1}{2} r^2 \theta. \label{sectorarea} \]

Finding the areas of sectors becomes increasingly essential as you move into Calculus (specifically, Integral Calculus). Be sure to spend the time now to master this relatively straightforward concept.

Example \(\PageIndex{1}\)

Find the area of the sector subtended by a central angle of \( 120^{ \circ } \) in a circle of radius \( 4 \).

Solution

The most common mistake when using Equation \ref{sectorarea} is not working in radian measure. Since \( 120^{ \circ } = \frac{2 \pi}{3} \), we find the area of the sector to be\[ A = \dfrac{1}{2}\cdot (4)^2 \left( \dfrac{2\pi}{3} \right) = \dfrac{16 \pi}{3}. \nonumber \]

Checkpoint \(\PageIndex{1}\)

If the area of a sector of a circle having radius \( 12 \) meters is \( 100 \) square meters, find the measure of the central angle (in radians).

Answer

\( \frac{25}{18} \) radians

Example \(\PageIndex{2}\): The Midnight Sun Golf Challenge

In certain parts of the world near the Arctic, such as Norway, the sun doesn't set during part of the summer. This phenomenon is known as the Midnight Sun. A golf course in Norway takes advantage of this by hosting a special event: The Midnight Sun Golf Challenge. During this event, golfers can play as many holes as they want throughout the night.

The golf course has a unique challenge on their signature par 3 hole, which features a circular green with a radius of 15 meters. If a golfer lands their ball within a particular marked sector of the green, where the central angle is 30 degrees, they win a prize. To determine the likelihood of winning, calculate the area of the sector where golfers must land their ball.

Solution

We are given \( \theta = 30^{ \circ } = \frac{\pi}{6} \) radians and \( r = 15 \) meters. Therefore, the area of the sector is\[ A = \dfrac{1}{2} \cdot (15)^2 \dfrac{\pi}{6} = \dfrac{225\pi}{12} \approx 59 \, \text{square meters} \nonumber \]As an aside, the probability that the golfer's ball would land in this sector (given the ball lands on the green and that all areas are equally likely for the ball to land in) would be the ratio of this sector area to the area of the entire green, which is\[ \dfrac{A_{\text{sector}}}{A_{\text{green}}} = \dfrac{225 \pi / 12}{\pi (15)^2} = \frac{1}{12} \approx 0.083 = 8.3\%. \nonumber \]This should make sense because \( 30^{ \circ } \) is one-twelfth of a full rotation of a circle.

Checkpoint \(\PageIndex{2}\)

A circular park has a sector fenced off for dogs. The sign posted by Sacramento County states that dogs can enjoy 6,000 square feet of play area; however, Paige finds this claim rather dubious. Unafraid about how foolish she might look, Paige takes a very large tape measure to the park and measures the radius of the park to be 120 feet. She then measures the length of fencing along the arc of the dog park area to be roughly 84 feet. Is the sign claiming that dogs have 6,000 square feet of play area correct?

Answer

No. The given measurements yield a central angle of \( 0.7 \) radians. Thus, the area is actually\[ A = \dfrac{1}{2} (120)^2 (0.7) = 5,040 \, \text{square feet}. \nonumber \]

Linear Motion

We have already used the variable \( s \) to denote the arc length in a circle of radius \( r \) subtended by a central angle \( \theta \). We might not have mentioned that this same variable is used throughout Mathematics and Physics to denote spatial position (hence, the letter \( s \)). For example, in Algebra and Calculus, you might represent the height of a projectile (relative to the ground) at any time \( t \) by the function\[ s(t) = -16t^2 + 20t +5. \nonumber \]Note that we have used the words spatial position and height to represent the same thing. In truth, "height" only applies if an object rises or falls relative to some point in space. "Spatial position," on the other hand, is a bit more flexible and allows us to consider the distance an object is away from a centralized point. Another word commonly used in place of spatial position is displacement.

Once we have a function for an object's spatial position (or displacement) at a given time \( t \), we can expand our investigation of the object's motion to include its velocity. In Physics, the average velocity (sometimes called the average linear velocity) of an object, denoted \(\overline{v}\) and read as "\(v\)-bar," is defined as the average rate of change of the spatial position of the object with respect to time. As a result, we have\[\overline{v} = \frac{\text{displacement}}{\text{time}} = \frac{s}{t}.\nonumber \]The quantity \(\overline{v}\) has units of \(\frac{\text{length}}{\text{time}}\) and conveys two ideas: the direction in which the object is moving and how fast the position of the object is changing. For example, if we define movement to the right as positive and movement to the left as negative, an object moving 10 feet to the right in 5 seconds has an average velocity over that period of\[ \overline{v} = \dfrac{+10 \, \text{feet}}{5 \, \text{seconds}} = 2 \, \text{feet per second}. \nonumber \]In this situation, we have written a plus sign on the 10 feet because the object is moving to the right by 10 feet over this period. On the other hand, if the object moving to the left at 10 feet for every 5 seconds, its average velocity over that period would be\[ \overline{v} = \dfrac{-10 \, \text{feet}}{5 \, \text{seconds}} = -2 \, \text{feet per second}. \nonumber \]If we could somehow measure the velocity of an object at a specific moment in time (rather than over an interval of time), we could call that the instantaneous velocity, \( v \). The instantaneous velocity of an object is often just called the velocity of the object.

It is a common mistake for people to confuse velocity with speed. The speed of an object is the magnitude of its instantaneous velocity. That is,\[ \text{speed} = \left| v \right|. \nonumber \]Note that speed is never negative, while velocity (and average velocity) can be negative (denoting both speed and direction).

Example \(\PageIndex{3}\)

Ants are incredibly fast, especially when you consider their size! The Saharan silver ant (Cataglyphis bombycina) holds the record for the fastest speed ever measured in an ant. It can move at a breathtaking 168.3 inches in five seconds. Find the average velocity of this ant.

Solution

Let \( s = 168.3 \) inches and \( t = 5 \) seconds. Then the average velocity of the Saharan silver ant is\[ \overline{v} = \dfrac{168.3 \, \text{inches}}{5 \, \text{seconds}} = 33.66 \, \text{inches per second}. \nonumber \]

Checkpoint \(\PageIndex{3}\)

Kenyan athlete Kelvin Kiptum set a men's world record time of 2:00:35 on October 8, 2023, at the 2023 Chicago Marathon (26.2 miles). Find his average velocity for the race in miles per hour. Round your answer to the nearest hundredth.

Answer

\(13.04\) miles per hour.

What if we wanted to know how fast the Kenyan athlete in Checkpoint \( \PageIndex{ 3 } \) was running at exactly 1 hour and 12 minutes into the marathon? That is, what if we wanted to know his instantaneous velocity at precisely 1 hour and 12 minutes into the marathon? We know that he had an average linear velocity of approximately 13.04 miles per hour; however, this does not mean he ran at 13.04 miles per hour the entire race. There were many moments when he ran faster than this and others when he ran slower. Since his velocity was not constant throughout the marathon, we would be hard-pressed to compute his instantaneous velocity at 1 hour and 12 minutes into the race - the answer to this type of question is the purview of Calculus.

Since we do not have Calculus at our disposal, if we ever want to answer a question about instantaneous velocity (again, which we call velocity), we must assume that the object's velocity is constant throughout the motion. Then, and only then, it can be shown that the average linear velocity is the same as the instantaneous velocity, \( v \). For the remainder of our discussion, we will make such an assumption. That is, from this sentence forward in this section, we will assume that the object, person, car, particle, or thing we are considering is moving at a constant speed. Hence, its average velocity is equivalent to its instantaneous velocity at any given moment. Again, we will simplify the wording to "velocity."

Circular Motion - Linear Velocity

Our next excursion into the realm of applications comes through circular motion. Suppose an object is moving as pictured below along a circular path of radius \(r\) from the point \(P\) to the point \(Q\) in an amount of time \(t\).

Like before, \(s\) represents a displacement so that \(s > 0\) means the object is traveling in a counter-clockwise direction, and \(s<0\) indicates movement in a clockwise direction. Note that with this convention, the formula we used to define radian measure, namely \(s = r \theta\), still holds since a negative value of \(s\) incurred from a clockwise displacement matches the negative we assign to \(\theta\) for a clockwise rotation.

Again, just as before, the quantity\[\overline{v} = \dfrac{s}{t} \nonumber \]is called the average linear velocity. This is despite the fact that \( s \) is a length along the curved edge of a circle. This is because if the path of the object were "uncurled" from a circle to form a line segment, then the average velocity of the object on that line segment would be the same as the average velocity on the circle.

Example \(\PageIndex{4}\)

As of 2024, the world's largest Ferris wheel is the Dubai Eye. It opened in 2021 on tiny Bluewaters Island in the Arabian Gulf. The diameter of the wheel is 820 feet, and a single rotation lasts 38 minutes. Assuming the wheel never stops turning, what is a rider's (instantaneous) linear velocity on the Dubai Eye?

Solution

We need to compute how far along the edge of the circle formed by the Dubai Eye that a rider moves through in a certain amount of time. Luckily, we were told a rider completes a full circuit in 38 minutes. Therefore, we let \( t = 38 \) minutes. Moreover, the distance traveled in that time is the same as the circumference of the circle. Here, we can use the faithful formula,\[ C = 2 \pi r. \nonumber \]The diameter of the Dubai Eye is 820 feet, so the radius is 410 feet. Thus, a rider travels a distance of \[ s = C = 2 \pi (410 \, \text{feet}) = 820 \pi \, \text{feet}. \nonumber \]We now use our velocity formula,\[ v = \dfrac{s}{t} = \dfrac{820 \pi \, \text{feet}}{38 \, \text{minutes}} \approx 67.8 \, \text{feet per minute}. \nonumber \]For reference, this is a glacial 0.8 miles per hour.

Example \( \PageIndex{ 4 } \) showcases that computing the linear velocity of an object along a circular path is very much the same as computing the velocity along a line, we just compute \( \frac{\text{distance}}{\text{time}} = \frac{s}{t} \).

Checkpoint \(\PageIndex{4}\)

Gum gets stuck to the outer edge of your bike tire. Suppose the tire rotates so that the gum travels along the circular path of its edge 5 inches in 2 seconds. What is the linear velocity of the gum? (By the way, this is also the linear speed of the tire.)

Answer

\( v = 2.5 \) inches per second

Circular Motion - Angular Velocity

Dividing both sides of \( s = r \theta \) by \( t \), we get a very powerful relation:\[\dfrac{s}{t} = \dfrac{r \theta}{t} \implies v = r \cdot \dfrac{\theta}{t}\nonumber\]The quantity \(\frac{\theta}{t}\) is called the average angular velocity of the object. If the rate of change of the angle \( \theta \) with respect to time is constant (which it will be for our purposes), then it is called the angular velocity, and it is denoted by \(\omega\) (omega). The quantity \(\omega\) has units \(\frac{\text{radians}}{\text{time}}\).

Example \(\PageIndex{5}\)

A point on a circle rotates through \( 38^{ \circ } \) in 3 hours. What is the angular velocity of the point?

Solution

Remember that the formula, \( s = r \theta \), requires \( \theta \) to be in radians. This is the same \( \theta \) as the angle in \( \omega = \frac{\theta}{t} \). Therefore, we need to convert the given angle to radians.\[ \omega = \dfrac{38^{ \circ }}{3\, \text{hours}} = \dfrac{38\pi \, \text{radians}}{540\,\text{hours}} \approx 0.2211 \, \text{radians per hour}. \nonumber \]

Checkpoint \(\PageIndex{5}\)

Suppose a point on a circle rotates through \( 300^{ \circ } \) in two hours. Find the exact value of the angular velocity of the point.

Answer

\( \frac{5\pi}{6} \) radians per hour

Circular Motion - Relating Linear and Angular Velocities

We now formalize our recent statement.

Theorem: Velocity for Circular Motion

For an object moving on a circular path of radius \(r\) with constant angular velocity \(\omega\), the (linear) velocity of the object is given by\[v = r \omega. \nonumber \]

We need to talk about units here. The units of \(v\) are \(\frac{\text{length}}{\text{time}}\), the units of \(r\) are length only, and the units of \(\omega\) are \(\frac{\text{radians}}{\text{time}}\). Thus the left hand side of the equation \(v = r \omega\) has units \(\frac{\text{length}}{\text{time}}\), whereas the right hand side has units \(\text{length} \cdot \frac{\text{radians}}{\text{time}} = \frac{\text{length} \cdot \text{radians}}{\text{time}}\). The supposed contradiction in units is resolved by remembering that radians are a dimensionless quantity and angles in radian measure are identified with real numbers so that the units \(\frac{\text{length} \cdot \text{radians}}{\text{time}}\) reduce to the units \(\frac{\text{length}}{\text{time}}\). We are long overdue for an example.

Example \( \PageIndex{6} \)

Assuming that the surface of the Earth is a sphere, any point on the Earth can be thought of as an object traveling on a circle which completes one revolution in (approximately) 24 hours. The path traced out by the point during these 24 hours is the latitude of that point. Cosumnes River College is at \(38^{\circ} \, 27^{\prime} \, 14.07^{\prime\prime}\) north latitude, and it can be shown that the radius of the Earth at this latitude is approximately \(3958\) miles. Find the linear velocity, in miles per hour, of Cosumnes River College as the world turns.

Solution

To use the formula \(v = r \omega\), we first need to compute the angular velocity \(\omega\). The Earth makes one revolution in 24 hours. One revolution is \(2 \pi\) radians, so\[\omega = \dfrac{2 \pi \, \text{radians}}{24 \, \text{hours}} = \frac{\pi}{12 \, \text{hours}},\nonumber \]where, once again, we are using the fact that radians are real numbers and are dimensionless. (For simplicity’s sake, we are also assuming that we are viewing the rotation of the Earth as counter-clockwise, so \(\omega > 0\).) Hence, the linear velocity is\[v = 3958 \, \text{miles} \cdot \frac{\pi}{12 \, \text{hours}} \approx 1036 \, \frac{\text{miles}}{\text{hour}}\nonumber\]

Checkpoint \(\PageIndex{6}\)

How fast is a bike moving, in miles per hour, if its rear tire has a radius of 15 inches and the angular velocity of the rear tire is 20 radians per second?

Answer

\( \approx 17 \) miles per hour

It is worth noting that the quantity \(\frac{1 \, \text{revolution}}{24 \, \text{hours}}\) in Example \( \PageIndex{5} \) is called the ordinary frequency of the motion and is usually denoted by the variable \(f\). The ordinary frequency is a measure of how often an object makes a complete cycle of the motion. The fact that \(\omega = 2\pi f\) suggests that \(\omega\) is also a frequency. Indeed, it is called the angular frequency of the motion. On a related note, the quantity \(T = \frac{1}{f}\) is called the period of the motion and is the amount of time it takes for the object to complete one cycle of the motion. In the scenario of Example \( \PageIndex{5} \), the period of the motion is 24 hours, or one day.

The concepts of frequency and period help frame the equation \(v = r \omega\) in a new light. That is, if \(\omega\) is fixed, points which are farther from the center of rotation need to travel faster to maintain the same angular frequency since they have farther to travel to make one revolution in one period’s time. The distance of the object to the center of rotation is the radius of the circle, \(r\), and is the "magnification factor," which relates \(\omega\) and \(v\). We will have more to say about frequencies and periods later in this text.

We close out this section with a beautiful application requiring great attention to detail.

Example \(\PageIndex{7}\)

A bicycle with a 27-inch-diameter rear wheel has its gears set so that the chainring has a 4-inch diameter and the rear sprocket has a 3-inch diameter (see image below). The cyclist pedals at 250 rpm. What is the speed of the bicycle in miles per hour?

Solution

In a complex problem like this, it's best to collect the given data by object. That is, we will have data for the chainring, the sprocket, and the rear wheel. We might not use all of these objects in our computations, but just listing them out is often helpful.\[ \begin{array}{rccc}
& \mathbf{Chainring} & \mathbf{Sprocket} & \mathbf{Wheel} \\
\hline \mathbf{Radius} & r_c = 2 \, \text{inches} & r_s = 1.5 \, \text{inches} & r_w = 13.5 \, \text{inches} \\
\mathbf{Linear Velocity} & v_c = ? & v_s = ? & v_w = ? \\
\mathbf{Angular Velocity} & \omega_c = ? & \omega_s = ? & \omega_w = ? \\
\end{array} \nonumber \]Before we get into computations, a little bit of logic is helpful. First, how quickly the sprocket is spinning should match how quickly the rear wheel is spinning (in angles per unit time). Therefore, \( \omega_s = \omega_w \). Additionally, we were told the cyclist is pedaling at 250 rpm (revolutions per minute). Thus, the chainring (which the pedal is attached to) is spinning at 250 rpm. We need to convert this to "radians per minute" using the fact that there are \( 2\pi \) radians per revolution. Therefore,\[ 250 \, \text{rpm} = \dfrac{250 \, \text{revolutions}}{\text{minute}} = \dfrac{250 \, \cancel{\text{revolutions}}}{\text{minute}} \cdot \dfrac{2 \pi \, \text{radians}}{\cancel{\text{revolution}}} = \dfrac{500 \pi \, \text{radians}}{\text{minute}}. \nonumber \]Notice that we kept the word "radians" in this computation. It's not necessary to do this, but it allows us to easily interpret the meaning of the quantity we are working with. At this point, let's update our table.\[ \begin{array}{rccc}
& \mathbf{Chainring} & \mathbf{Sprocket} & \mathbf{Wheel} \\
\hline \mathbf{Radius} & r_c = 2 \, \text{inches} & r_s = 1.5 \, \text{inches} & r_w = 13.5 \, \text{inches} \\
\mathbf{Linear Velocity} & v_c = ? & v_s = ? & v_w = ? \\
\mathbf{Angular Velocity} & \omega_c = 500 \pi \, \dfrac{\text{radians}}{\text{minute}} & \omega_s = \omega_w & \omega_w = \omega_s \\
\end{array} \nonumber \]We now use the completed information about the chainring (the radius and angular velocity) to find the linear velocity of a point on the edge of the chainring.\[ v_c = r_c \omega_c = (2 \, \text{inches}) ( 500 \pi \, \text{radians/minute}) = 1000 \pi \, \dfrac{\text{inches}}{\text{minute}} \nonumber \]Remember, radians is a unitless measure. Since a point along the edge of the chainring is just a link in the chain connecting the chainring to the sprocket, this will also be the linear velocity of a link moving along the edge of the sprocket. Thus, our table gets updated to the following.\[ \begin{array}{rccc}
& \mathbf{Chainring} & \mathbf{Sprocket} & \mathbf{Wheel} \\
\hline \mathbf{Radius} & r_c = 2 \, \text{inches} & r_s = 1.5 \, \text{inches} & r_w = 13.5 \, \text{inches} \\
\mathbf{Linear Velocity} & v_c = 1000 \pi \, \dfrac{\text{inches}}{\text{minute}} & v_s = 1000 \pi \, \dfrac{\text{inches}}{\text{minute}} & v_w = ? \\
\mathbf{Angular Velocity} & \omega_c = 500 \pi \, \dfrac{\text{radians}}{\text{minute}} & \omega_s = \omega_w & \omega_w = \omega_s \\
\end{array} \nonumber \]We now can find the angular velocity of the sprocket.\[ v_s = r_s \omega_s \implies \omega_s = \dfrac{v_s}{r_s} = \dfrac{1000 \pi \, \cancel{\text{inches}}\text{/minute}}{1.5 \, \cancel{\text{inches}}} = \dfrac{2000 \pi}{3} \, \dfrac{\text{radians}}{\text{minute}} \nonumber \]Again, this angular velocity is exactly the same as the angular velocity of the wheel. Thus, our table becomes\[ \begin{array}{rccc}
& \mathbf{Chainring} & \mathbf{Sprocket} & \mathbf{Wheel} \\
\hline \mathbf{Radius} & r_c = 2 \, \text{inches} & r_s = 1.5 \, \text{inches} & r_w = 13.5 \, \text{inches} \\
\mathbf{Linear Velocity} & v_c = 1000 \pi \, \dfrac{\text{inches}}{\text{minute}} & v_s = 1000 \pi \, \dfrac{\text{inches}}{\text{minute}} & v_w = ? \\
\mathbf{Angular Velocity} & \omega_c = 500 \pi \, \dfrac{\text{radians}}{\text{minute}} & \omega_s = \dfrac{2000\pi}{3} \, \dfrac{\text{radians}}{\text{minute}} & \omega_w = \dfrac{2000\pi}{3} \, \dfrac{\text{radians}}{\text{minute}} \\
\end{array} \nonumber \]We finally arrive at the penultimate computation - the linear velocity of the wheel.\[ v_w = r_w \omega_w = (13.5 \, \text{inches}) \left(\dfrac{2000\pi}{3} \, \dfrac{\text{radians}}{\text{minute}}\right) = 9000 \pi \, \dfrac{\text{inches}}{\text{minute}} \nonumber \]Did you know the word "penultimate" means "second-to-last?" This means we have one more step (the ultimate step?). First, the linear velocity of a point on the wheel gives the velocity of the bicycle; however, this is in inches per minute and we were asked to find the answer in miles per hour. This is a nice unit analysis problem. Let's convert the distance units first.\[ 9000 \pi \, \dfrac{\cancel{\text{inches}}}{\text{minute}} \cdot \dfrac{\cancel{\text{foot}}}{12 \, \cancel{\text{inches}}} \cdot \dfrac{\text{mile}}{5280 \, \cancel{\text{feet}}} = \dfrac{9000 \pi}{(12)(5280)} \, \dfrac{\text{miles}}{\text{minute}} \nonumber \]Now let's convert the time units.\[\dfrac{9000 \pi}{(12)(5280)} \, \dfrac{\text{miles}}{\cancel{\text{minute}}} \cdot \dfrac{60 \, \cancel{\text{minutes}}}{\text{hour}} = \dfrac{(9000\pi)(60)}{(12)(5280)} \, \text{mph} \approx 26.8 \, \text{mph} \nonumber \]

Checkpoint \(\PageIndex{7}\)

If the chainring of a bicycle is 150 mm in diameter, the sprocket is 80 mm in diameter, and the wheel is 700 mm in diameter, how fast would one need to pedal, in revolutions per minute, in order to maintain a speed of 24 kilometers per hour?

Answer

Approximately 97 rpm.

---

Skills Refresher

Review the following skills you will need for this section.

Skills Refresher

We need algebra refresher problems. Maybe unit conversion problems and \(d = rt\) or \(v = s/t\) problems?

---

Homework

Vocabulary Check

1. The region bounded by the initial and terminal sides of a central angle \( \theta \) and the edge of the circle is called a ___ of a circle.

2. A word commonly used in place of spatial position is ___.

3. The ___ of a particle is the average rate of change of its position with respect to a change in time. If we could take an instantaneous "snapshot" of this form of motion, we would call it the ___ of the particle.

4. The ___ of a particle is the magnitude of its velocity.

Concept Check

5. Write each statement as a mathematical formula.

   1. The length of the arc, \(s\), is equal to:\[\text{(the fraction of a revolution)} \times \text{(circumference of the circle)} \nonumber \]

   2. The area of the sector, \(A\), is equal to:\[\text{(the fraction of a revolution)} \times \text{(area of the circle)}\nonumber \]

True or False? For Problems 6 - 7, determine if the statement is true or false. If true, cite the definition or theorem stated in the text supporting your claim. If false, explain why it is false and, if possible, correct the statement.

6. To compute the area of a sector, we multiply the given angle by half of the square of the circle's radius.

7. Given two circles, one of radius \( r_1 \) and the other of radius \( r_2 \), particles on each circle moving at a constant angular velocity, \( \omega \), move at the same linear velocity.

Basic Skills

For Problems 8 - 16, \( \theta \) is the central angle in a circle of radius \( r \). In each case, find the area of the circle.

8. \( \theta = \frac{2 \pi}{3}, \qquad r = 7 \, \text{yards} \)

9. \( \theta = \frac{7 \pi}{6}, \qquad r = \sqrt{2} \, \text{m} \)

10. \( \theta = \frac{6 \pi}{7}, \qquad r = \sqrt{3} \, \text{miles} \)

11. \( \theta = 3, \qquad r = \frac{1}{2} \)

12. \( \theta = 5, \qquad r = 4.1 \, \text{cm} \)

13. \( \theta = 60^{ \circ }, \qquad r = 2 \, \text{feet}\)

14. \( \theta = 330^{ \circ }, \qquad r = \pi \, \text{inches} \)

15. \( \theta = 32^{ \circ }, \qquad r = 8 \, \text{parsecs} \)

16. \( \theta = 212^{ \circ }, \qquad r = 0.88 \, \text{leagues} \)

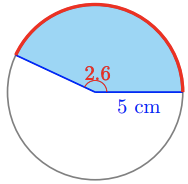
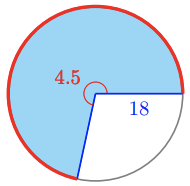
For Problems 17 - 18, find the area of the shaded sector.

17.  

    

18.  

    

Determining Areas of Sectors

17. An arc of length 8 feet is cut off by a central angle of \( 2\pi/3 \) radians. Find the area of the resulting sector.

18. A central angle of 4 radians cuts off an arc of length 16 meters. Find the area of the resulting sector.

19. Calculate the area of a sector with a radius of 6 cm and a central angle of \( 30^{ \circ } \).

20. A sector has a radius of 4 meters and a central angle of \( 45^{ \circ } \). Find its area.

21. If the radius of a sector is 10 inches and the central angle is \( 60^{ \circ } \), what is the area of the sector?

22. Determine the area of a sector with a radius of 8 feet and central angle \( 2\pi/3 \).

23. Calculate the area of a sector with a 3-meter radius and central angle \( 5\pi/6 \).

Determining the Radius of a Sector

24. If the area of a sector is 25 cm² and the central angle is \( 45^{ \circ } \), find the radius.

25. Determine the radius of a sector with an area of 30 m² and a central angle of 60 degrees.

26. A sector has an area of 14 in² and central angle \( \pi/6 \). What is its radius?

27. What is the radius of a sector with an area of 78 cm² and a central angle of 120 degrees?

28. What is the radius of a sector if the area is 100 cm² and the central angle is 250 degrees?

Determining the Central Angle of a Sector

29. Find the radian measure of the central angle of a sector with a radius of 5 cm and an area of 20 cm².

30. Determine the radian measure of the central angle if a sector has a radius of 3 meters and an area of 15 m².

31. What is the degree measure of the central angle of a sector with a radius of 7 inches and an area of 24 in²?

32. Calculate the degree measure of the central angle for a sector with a radius of 10 feet and an area of 50 ft².

33. Calculate the degree measure of the central angle for a sector with a radius of 11 cm and an area of 30.25 cm².

Determining Angular Velocity

34. Wheel Rotation. If a wheel rotates 300 times in one minute, find its angular velocity in radians per second.

35. Merry-go-Round. How many complete revolutions does a merry-go-round make in 10 minutes if it has an angular velocity of 0.5 radians per second?

36. Mixing Machine. A mixing blade in a blender rotates at 1200 revolutions per minute. Calculate its angular velocity in radians per second.

37. Computer Hard Drive. The spindle of a computer hard drive spins at 7200 RPM. What is the angular velocity of the spindle in radians per second?

38. Electric Generator. An electric generator's rotor spins at 3600 revolutions per minute. Determine the rotor's angular velocity in radians per second.

39. Laundry Machine. During the spin cycle, a washing machine drum rotates at 800 revolutions per minute. Calculate the angular velocity in radians per second.

40. Vehicle's Alternator. The alternator in a car operates at 6000 RPM when the engine is at full speed. Find the angular velocity of the alternator in radians per second.

Converting Between Linear and Angular Velocities

41. Bike Tire. A bicycle tire has a radius of 35 cm. If the tire rotates at an angular velocity of 2 radians per second, calculate the linear velocity of a point on the tire’s rim.

42. Circular Machinery. A part of a machine moves in a circle of radius 15 cm at a constant speed. If the linear velocity of the part is 90 cm/s, calculate its angular velocity in radians per second.

43. Ceiling Fan Speed. The blade of a ceiling fan is 0.7 meters long from the center to the tip. If the tip of the blade moves at a linear velocity of 4.5 meters per second, calculate the angular velocity of the blade in radians per second.

44. Amusement Park Ride. A merry-go-round has a radius of 5 meters. If a horse on the edge of the ride moves at a linear velocity of 3 meters per second, find the angular velocity of the merry-go-round in radians per second.

45. Industrial Flywheel. An industrial flywheel has a radius of 2 meters. If it is required to achieve a linear speed of 10 meters per second at its rim, determine the necessary angular velocity in radians per second.

46. Athletics Track Runner. A runner is jogging along a circular track with a radius of 25 meters, maintaining a constant linear speed of 2.5 meters per second. Calculate the runner’s angular velocity in radians per second.

47. Spinning Top. A spinning top has a radius of 8 cm. If the linear velocity of a point on its edge is 1.6 meters per second during a spin, what is the angular velocity of the top in radians per second?

48. Windmill Blades. A windmill's blade has an angular velocity of 0.8 radians per second and each blade is 3 meters long. Calculate the linear velocity at the tip of a blade.

49. Rotating Sign. A circular sign rotates at an angular velocity of 2 radians per second. If the radius of the sign is 1.5 meters, what is the linear velocity of the edge of the sign?

50. Gear in a Machine. A gear in a factory machine has a radius of 20 cm and rotates with an angular velocity of 5 radians per second. Determine the linear velocity of a point on the edge of the gear.

51. Carousel Horse. A carousel horse moves in a circular path with a radius of 4 meters. If the angular velocity of the carousel is 1 radian per second, find the linear velocity of the horse.

52. Bicycle Pedaling Speed. A bicycle's pedal arm is 17.5 cm long, and the cyclist is pedaling at an angular velocity of 4 radians per second. Calculate the linear velocity at the end of the pedal arm.

Synthesis Questions

53. Calculate the radius of a sector whose area is one-fifth of the area of a circle with a radius of 10 cm.

54. Determine the radius of a sector if its area is equivalent to half the area of a circle with a radius of 14 meters.

55. Two circular saw blades are spinning, one at 120 RPM and the other at 180 RPM. If both blades have a diameter of 30 cm, which blade has a higher linear velocity at the rim, and by how much?

Applications

Sector Area Applications

56. Land Allocation. A farmer plans to allocate a portion of his circular field for a special crop. The field has a radius of 100 meters. If he uses a 60-degree sector for this crop, calculate the area that will be cultivated.

57. Clock Face Design. A designer is creating a new clock face where each hour marker is represented by a different colored sector. The clock has a radius of 12 cm. Calculate the area of one hour sector assuming a simple 12-hour clock.

58. Architectural Design. An architect designs a circular window with decorative sectors. Each sector has a central angle of 45 degrees and the window has a diameter of 2 meters. Calculate the area of one decorative sector.

59. City Planning. A city planner needs to design a roundabout garden that occupies a 38-degree sector of a circle with a radius of 20 meters. Calculate the area available for planting.

60. Pizza Slicing. A pizza place offers a unique pizza slice shaped as a sector. The pizza has a diameter of 40 cm. If the central angle for each slice is 20 degrees, find the area of one slice of pizza.

61. Sports Fields. A sports complex includes a sector-shaped running track portion used for sprinting drills. If the track follows a 40-degree sector of a circle with a radius of 100 meters, calculate the area of this track section.

62. Public Park Design. A public park is designed with a circular area for a water fountain, surrounded by flower beds laid out in sectors. If the circular area has a radius of 15 meters and each sector for the flower beds is 30 degrees, find the area of one flower bed.

63. Non-Uniform Rainfall. A circular region with a radius of 20 km receives rainfall. However, the rain is not uniformly distributed. If a 120-degree sector receives twice the amount of rain per square kilometer as the rest of the region, calculate the total rainfall if the sector received 600 mm.

64. Engineering Design. An engineer is designing a gear in the shape of a sector. The gear must mesh with another gear with an area three times larger but with the same arc length. If the radius of the smaller gear is 15 cm, determine the central angle of the sector for the smaller gear.

65. Advanced Pizza Slicing. A circular pizza is sliced such that each consecutive slice has a central angle 10 degrees greater than the previous one, starting from 10 degrees. Calculate the area of the 5^th slice if the pizza has a radius of 30 cm.

66. Sector-based Cooling Zones. A circular mechanical part is designed with cooling zones in the form of sectors. Each zone dissipates heat differently. If one zone with a 60-degree angle dissipates heat at 100 watts per square meter and the radius of the part is 30 cm, find the total heat dissipation for this zone.
    (Hint: Heat dissipation is the total number of watts of heat released in a given area.)

Velocity Applications

67. Find the angular velocity of the following objects.

    1. The London Eye Ferris wheel, which makes one revolution every 20 minutes.

    2. An old-fashioned long-playing record, which revolved \(33 \frac{1}{3}\) times in 60 seconds.

68. Conveyor Belt. A conveyor belt moves at a linear velocity of 1.5 meters per second. If the driving drum has a radius of 0.5 meters, calculate the angular velocity of the drum in radians per second.

69. Bike Wheel Spin. A bicycle wheel has a radius of 0.4 meters. If the wheel is spinning with an angular velocity of 5 radians per second, what is the linear velocity of a point on the rim?

70. Rollerblade Wheel. A rollerblade wheel has a radius of 40 mm. If a rollerblader is moving at a linear speed of 10 km/h, find the angular velocity of the wheels in radians per second.

71. Ferris Wheel. A Ferris wheel has a radius of 25 meters and rotates at a linear velocity of 2 meters per second at its rim. Calculate its angular velocity in radians per second.

72. Car Tire Rotation. A car tire has a radius of 35 cm. If the car is traveling at 80 km/h, find the angular velocity of the tire in radians per second.

73. Potter’s Wheel Speed. If the edge of a potter's wheel moves at a linear velocity of 15 m/s and the wheel has a radius of 1.2 meters, determine the angular velocity in radians per second.

74. Drill Bit Rotation. A drill bit has a radius of 1 cm. If it needs to achieve a linear velocity of 20 m/s at its tip, calculate the required angular velocity in radians per second.

75. Record Player. If a point on a record player is moving with a linear velocity of 0.5 m/s and the record has a radius of 15 cm, what is the angular velocity in radians per second?

76. Electric Fan. An electric fan has blades that are each 0.25 meters long. If a point on the tip of a blade moves with a linear velocity of 3 m/s, what is the angular velocity of the blades in radians per second?

77. Satellite Dish Rotation. A satellite dish has a radius of 2 meters. If it rotates such that a point on its edge moves at a linear velocity of 0.1 m/s, calculate the angular velocity in radians per second.

78. Fan Speed. A ceiling fan has blades that are each 0.75 meters long. If the fan spins at 200 revolutions per minute (RPM), calculate the angular velocity in radians per second.

79. Merry-Go-Round. Children are riding on a merry-go-round that has a radius of 2 meters and makes one complete rotation every 4 seconds. Find the angular velocity in radians per second.

80. Driving Speed and Wheel Rotation. A car with wheels of radius 30 cm is traveling at a speed of 60 km/h. Calculate the angular velocity of the wheels in radians per second.

81. Bicycle Dynamics. A bicycle's front wheel has a diameter of 70 cm and rotates at 150 RPM while cruising. Determine the linear velocity of the bicycle.

82. Angular Velocity of a Clock's Second Hand. Calculate the angular velocity in radians per hour of the second hand of a clock.

83. Disk Rotation. A disk in a laboratory experiment rotates at a speed of 600 RPM. Calculate its angular velocity in radians per second.

84. Jogging on a Track. A jogger runs around a circular track with a diameter of 200 meters at a speed of 8 km/h. Compute the angular velocity of the jogger in radians per hour.

85. Wheelchair Wheel Rotations. A wheelchair has wheels of diameter 60 cm. If a person moves at a speed of 4 km/h, determine the angular velocity of the wheels in radians per second.

86. Spinner Toy. A spinner toy rotates 4000 times in one minute. Calculate its angular velocity in radians per second.

87. Record Player. A record player spins a record at 33 revolutions per minute. Find the angular velocity in radians per second and the linear velocity at a point 10 cm from the center.

88. Dryer. Clothes dryers draw 3.5 times as much power as washing machines, so newer machines have been engineered for greater efficiency. A vigorous spin cycle reduces the time needed for drying, and some front-loading models spin at a rate of 1500 rotations per minute.

    1. If the radius of the drum is 11 inches, how far do your socks travel in one minute?

    2. How fast are your socks traveling during the spin cycle?

89. Hubble Telescope. The Hubble telescope is in orbit around the earth at an altitude of 600 kilometers, and completes one orbit in 97 minutes.

    1. How far does the telescope travel in one hour? (The radius of the earth is 6400 kilometers.)

    2. What is the speed of the Hubble telescope?

90. Energy-Producing Windmill. The first large windmill used to generate electricity was built in Cleveland, Ohio in 1888. Its sails were 17 meters in diameter, and moved at 10 rotations per minute. How fast did the ends of the sails travel?

91. Largest Windmill. The largest windmill operating today has wings 54 meters in length. To be most efficient, the tips of the wings must travel at 50 meters per second. How fast must the wings rotate?

92. Planetary Motion. Assume a simplified model where a planet moves in a circular orbit around its star with a constant angular velocity. If the radius of the orbit is \( 1.5 \times 10^6 \) kilometers and it completes one orbit in 215 days, find the linear velocity of the planet.

93. Wheel Rotation. A car's tire has a diameter of 60 cm. If the car is traveling at a speed of 72 km/h, calculate the angular velocity of the tire in radians per second.

94. CD Player Speed. A CD rotates at 500 revolutions per minute (RPM) when playing. What is the linear velocity at a point 3 cm from the center of the CD?

95. Angular Speed of a Wind Turbine. A wind turbine blade is 45 meters long, and it completes one rotation every three seconds. Calculate the angular velocity in radians per second and the linear velocity at the tip of the blade.

96. Bicycle Wheel Dynamics. A bicycle wheel has a radius of 35 cm. If the bicycle is moving at a speed of 15 km/h, find the wheel’s angular velocity in radians per second.

97. Roller Coaster Speed. A roller coaster moves in a vertical loop of radius 12 meters at a speed of 36 km/h at the highest point of the loop. Calculate the angular velocity at this point.

98. Flywheel Operation. A flywheel in a machine spins at 1800 RPM. If the radius of the flywheel is 20 cm, calculate the linear velocity at the edge of the flywheel.

99. Satellite Orbiting. A satellite orbits the Earth in a circular path with a radius of 10,000 km at a constant speed of 7 km/s. Determine the angular velocity of the satellite in radians per hour.

100. Speed of a Ferris Wheel. A Ferris wheel with a diameter of 100 meters takes 4 minutes to make one complete revolution. Calculate the linear velocity and angular velocity of a cabin at the edge of the Ferris wheel.

101. Potter’s Wheel. A potter’s wheel moves from rest to an angular speed of 120 RPM in 5 seconds. Calculate the angular acceleration and the linear velocity at a point 15 cm from the center at the end of 5 seconds.

102. Circular Saw. A circular saw blade has a radius of 15 cm and rotates at a speed of 3000 RPM. Find the angular velocity in radians per second and the linear velocity at the perimeter of the blade.

Challenge Problems

103. If the radius of a sector is doubled while the central angle remains the same, by what factor does the area increase?