8.1: Arithmetic Sequences

Last updated
Save as PDF

Page ID: 83157

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The following sequence of numbers has a pattern you are bound to recognize:

$2, 4, 6, 8, 10, 12, 14, 16, 18, …$

Likely, you would describe the sequence in words: the sequence of even numbers. Alternatively, can we describe the sequence mathematically? That is, can we describe the pattern of the sequence of even numbers using a formula? Absolutely! This section will explore arithmetic sequences, how to identify them, mathematically describe their terms, and the relationship between arithmetic sequences and linear functions. Let’s get started!

Definition: Sequence

A sequence is a list of numbers: $a_1 , a_2, a_3, a_4 , … , a_n, … $ A sequence can be a finite or infinite list. We call $a_1$ the first term, $a_2$ the second term, and $a_n$ the “general term” or the $n^{\text{th}}$ term. Sequences have a pattern. We describe the pattern in the general term $a_n$.

For the sequence of even numbers: $2, 4, 6, 8, 10, …$ the general term $a_n = 2n$.

$clipboard_eddc57d00c36a2fbed49c43f696c7302b.png$

The general term $a_n$ of a sequence is simply a function of $n$, indicated above as $f(n)$, where $n$ is a natural number (or whole number if $n$ starts with zero).

Example 8.1.1

In the sequence of even numbers, what is the $20^{\text{th}}$ term in the sequence?

Solution

The general term of the sequence of even numbers is $a_n = 2n$. Since $n =$ the term number, we are asked to find $a_{20}$.

$\begin{array}&& a_{20} = 2(20) = 40 &\text{Plug in the term-number \(n=20$ into the formula $a_n=2n$} \end{array}\)

Answer The $20^{\text{th}}$ term of the sequence of even numbers is the number $40$.

Definition: Arithmetic Sequence

If the sequence: $a_1, a_2, a_3, a_4 , … , a_{n−1}, a_n, …$ exhibits a pattern such that

\[a_n − a_{n−1} = d\]

For all $n$, then the real number $d$ is called the common difference, and the sequence is an arithmetic sequence.

Example 8.1.2

A sequence is given. If the sequence is an arithmetic sequence, give the common difference. If the sequence is not an arithmetic sequence, explain how it fails to be arithmetic.

$25, 32, 39, 46, 53, 60, …$
$2, 4, 8, 16, 32, …$
$3^2 , 3^4, 3^6, 3^8, 3^{10}, …$
$0, 1, 0, 1, 0, 1, …$

Solution

Is the sequence

$25, 32, 39, 46, 53, 60, … $

an arithmetic sequence?

$\begin{array} &a_2 − a_1 &= 32 − 25 &= \textcolor{red}{7} \\ a_3 − a_2 &= 39 − 32 &= \textcolor{red}{7} \\a_4 − a_3 &= 46 − 39 &= \textcolor{red}{7} \\a_5 − a_4 &= 53 − 46 &= \textcolor{red}{7} \\a_6 − a_5 &= 60 − 53 &= \textcolor{red}{7} \end{array}$

The sequence is arithmetic and the common difference is $7$.

Is the sequence

$2, 4, 8, 16, 32, …$

an arithmetic sequence?

$\begin{array} &a_2 − a_1 &= 4 − 2 &= \textcolor{red}{2} \\ a_3 − a_2 &= 8 − 4 &= \textcolor{red}{4} \\a_4 − a_3 &= 16 − 8 &= \textcolor{red}{8} \\a_5 − a_4 &= 32 − 16 &= \textcolor{red}{16} \\ &&\textcolor{red}{2 \neq 4 \neq 8 \neq 16} \end{array}$

The sequence is not arithmetic. $a_n − a_{n-1}$ does not yield a common difference.

Is the sequence

$3^2 , 3^4, 3^6, 3^8, 3^{10}, …$

an arithmetic sequence?

$\begin{array} &3^4 − 3^2 &= 3^2 (3^2 − 1) &= 9 \cdot 8 &= \textcolor{red}{72} \\ 3^6 − 3^4 &= 3^4 (3^2 − 1) &= 81 \cdot 8 &= \textcolor{red}{648} \end{array}$

Since $a_3 − a_2 \neq a_2 − a_1$, we conclude the sequence is not arithmetic.

Is the sequence

$0, 1, 0, 1, 0, 1, …$

an arithmetic sequence?

$\begin{array} 1-0 &= \textcolor{red}{1} \\ 0-1 &= \textcolor{red}{-1} \end{array}$

Since $a_3 − a_2 \neq a_2 − a_1$, the sequence is not arithmetic.

Find the General Term of an Arithmetic Sequence

If a sequence is arithmetic, the general term $a_n$ is determined using the common difference, $d$, of the sequence. Functions of the form $y = mx+b$, known as linear functions, have a strong relationship to arithmetic sequences. The slope $m$ of a linear function is equivalent to the common difference $d$ of an arithmetic sequence. Let’s compare arithmetic sequences to linear functions to build $a_n$, the general term of an arithmetic sequence.

Example 8.1.3

Find the general term $a_n$ of each arithmetic sequence:

$4, 7, 10, 13, 16, …$
$100, 80, 60, 40, 20, …$

Solution

We will create a table of values for each sequence. The first column will be the term number, $n$, starting with $n = 1$. The second column will list the terms of the sequence. The common difference is shown on the side of the second column.

The sequence $4, 7, 10, 13, 16, …$ has the common difference $d = 3$. But it’s also the slope $m$ of the linear function $f(x) = mx + b$.

\[m = \dfrac{\delta y}{\delta x} = \dfrac{a_n − a_{n-1}}{n − (n − 1))} = \dfrac{d}{1} = d\]

$clipboard_ecbb8d4cf8b9fa5856cc56124c921e2e0.png$

The above table essentially mimics any linear function, $f(x) = mx+b$.

Instead of $x$, sequences use $n$−values.
Instead of $m =$ slope in linear functions, sequences use $d =$ common difference.
Instead of $b$, a sequence notates the same value with $a_0$.

If $a_1$ denotes the first term of a sequence, then the general term of a sequence is:

\[a_n = f(n) = d \cdot n + a_0\]

To find the general term, $a_n$, we will need to find the value $a_0$. There are several ways to do this, but perhaps the simplest is to create an extra row where $n = 0$, then use the common difference to find $a_0$. The common difference pattern is maintained and $a_0 + d = a_1$.

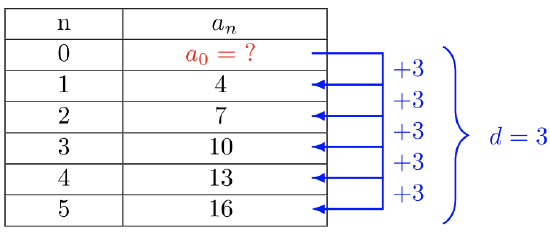
$clipboard_e6eccaea315b268044364f34c0948747d.png$

Find the value $a_0$:

$\begin{array} &&a_0 + 3 &= 4 \\&a_0 + 3 − 3 &= 4 − 3 \\&a_0 &= 1\end{array}$

The general term of the sequence is:

$a_n = 3n + 1$

Use the same strategy for Example $8.1.3$a to solve Example $8.1.3$b. Create a table, find the common difference, $d$, and find the $a_0$ term of the sequence $100, 80, 60, 40, 20, …$

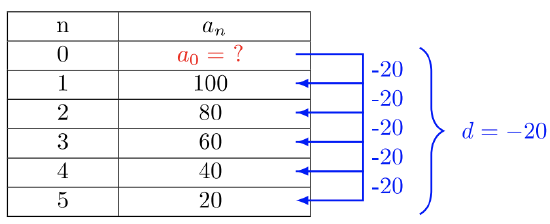
$clipboard_ee68ed069e37b2760f8fc0f27b5a37f04.png$

The common difference $d = −20$. Find the value $a_0$.

$\begin{array} &&a_0 − 20 &= 100 \\ &a_0 − 20 + 20 &= 100 + 20 \\ &a_0 &= 120 \end{array}$

The general term of the sequence is:

$a_n = −20n + 120$

Try It! (Exercises)

For #1-5, the general term of a sequence is given.

List the first $5$ terms of the sequence: $a_1, a_2, a_3, a_4, a_5$.
Is the sequence arithmetic?

$a_n = n^2$
$a_n = 4 − 5n$
$a_n = 2^n$
$a_n = \dfrac{1}{2}n$
$a_n = 0.3n + 1$

For #6-9, a table of values is given. State the general term, $a_n$, of the arithmetic sequence.

$n$	$a_n$
$1$	$9$
$2$	$15$
$3$	$21$
$4$	$25$

$n$	$a_n$
$1$	$42$
$2$	$38$
$3$	$34$
$4$	$30$

$n$	$a_n$
$1$	$7$
$2$	$7.25$
$3$	$7.5$
$4$	$7.75$

$n$	$a_n$
$1$	$65.4$
$2$	$52.2$
$3$	$39$
$4$	$25.8$

For #10-15, find the general term of the arithmetic sequence. Assume the first term is $a_1$.

$8, 15, 22, 29, …$
$110, 85, 60, 35, …$
$9, 7.4, 5.8, 4.2, …$
$\dfrac{17}{2} , 8, \dfrac{15}{2} , 7, …$
$−20, −8, 4, 16, 28, …$
$4 \dfrac{1}{2} , 5 \dfrac{1}{4} , 6, 6 \dfrac{3}{4} , …$

For #16-20, an arithmetic sequence is described. Find the general term $a_n$.

The arithmetic sequence has common difference $d=8$. The first term $a_1 = 28$.
The arithmetic sequence has first term $a_1 = 40$ and second term $a_2 = 36$.
The arithmetic sequence has first term $a_1 = 6$ and third term $a_3 = 24$.
The arithmetic sequence has common difference $d = −2$ and third term $a_3 = 15$.
The arithmetic sequence has common difference $d = 3.6$ and fifth term $a_5 = 10.2$.

Explain how the formula for the general term given in this section: $a_n = d \cdot n + a_0$ is equivalent to the following formula: $a_n = a_1 + d(n − 1)$
Some sequences have a finite number of terms. Find the number of terms in the finite arithmetic sequence: $3, 17, 31, … ,143$
Some sequences have a finite number of terms. Find the number of terms in the finite arithmetic sequence: $80, 69, 58, … , −52$
Create a formula for finding the number of terms a finite arithmetic sequence when given the first and the last term of the sequence. Assume the first term is $a_1$ and the last term is $a_k$.

\(n\)	\(a_n\)
\(1\)	\(9\)
\(2\)	\(15\)
\(3\)	\(21\)
\(4\)	\(25\)

\(n\)	\(a_n\)
\(1\)	\(42\)
\(2\)	\(38\)
\(3\)	\(34\)
\(4\)	\(30\)

\(n\)	\(a_n\)
\(1\)	\(7\)
\(2\)	\(7.25\)
\(3\)	\(7.5\)
\(4\)	\(7.75\)

\(n\)	\(a_n\)
\(1\)	\(65.4\)
\(2\)	\(52.2\)
\(3\)	\(39\)
\(4\)	\(25.8\)