8.2: Problem Solving with Arithmetic Sequences

Last updated
Save as PDF

Page ID: 83159

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Arithmetic sequences, introduced in Section 8.1, have many applications in mathematics and everyday life. This section explores those applications.

Example 8.2.1

A water tank develops a leak. Each week, the tank loses $5$ gallons of water due to the leak. Initially, the tank is full and contains $1500$ gallons.

How many gallons are in the tank $20$ weeks later?
How many weeks until the tank is half-full?
How many weeks until the tank is empty?

Solution

This problem can be viewed as either a linear function or as an arithmetic sequence. The table of values give us a few clues towards a formula.

$clipboard_e5c7552a37ec3c13691ea706a3d499232.png$

The problem allows us to begin the sequence at whatever $n$−value we wish. It’s most convenient to begin at $n = 0$ and set $a_0 = 1500$.

Therefore, $a_n = −5n + 1500$

How many gallons are in the tank $20$ weeks later?

Since the leak is first noticed in week one, $20$ weeks after the initial week corresponds with $n = 20$. Use the formula where $\textcolor{red}{n = 20}$:

$a_{20} = −5(\textcolor{red}{20}) + 1500 = −100 + 1500 = 1400$

Therefore, $20$ weeks later, the tank contains $1400$ gallons of water.

How many weeks until the tank is half-full? A half-full tank would be $750$ gallons. We need to find $n$ when $\textcolor{red}{a_n = 750}$.

$\begin{array} &750 &= −5n + 1500 &\text{Substitute \(a_n = 750$ into the general term.} \\ 750 − 1500 &= −5n + 1505 − 1500 &\text{Subtract $1500$ from each side of the equation.} \\ −750 &= −5n &\text{Simplify each side of the equation.} \\ \dfrac{−750}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by $−5$.} \\ 150 &= n & \end{array}\)

Since $n$ is the week-number, this answer tells us that on week $150$, the tank is half full. However, most people would better understand the answer if stated in the following way, “The tank is half full after 150 weeks.” This answer sounds more natural and is preferred.

How many weeks until the tank is empty? The tank is empty when $a_n = 0$ gallons. Find $n$ such that $\textcolor{red}{a_n = 0}$.

$\begin{array}& 0 &= −5n + 1500 &\text{Substitute \(a_n=0$ into the general term.} \\ 0 − 1500 &= −5n + 1500 − 1500 &\text{Subtract $1500$ from each side of the equation.} \\ −1500 &= −5n &\text{Simplify.} \\ \dfrac{−1500}{−5} &= \dfrac{−5n}{−5} &\text{Divide both sides by $−5$.} \\ 300 &= n & \end{array}\)

Since $n$ is the week-number, this answer tells us that on week $300$, the tank is empty. However, most people would better understand the answer if stated in the following way, “The tank is empty after 300 weeks.” This answer sounds more natural and is preferred.

Example 8.2.2

Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

How many matchsticks are required to make the figure in stage $34$?
What stage would require $220$ matchsticks?

Solution

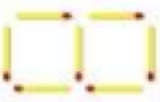$clipboard_e3cb0e75de710fefbbeea0c2d342f2609.png$	$clipboard_e64de99c72d853a3f4d859b06f4a881c2.png$	$clipboard_eb59659303898eeeca21851f42ece8e29.png$
Stage 1	Stage 2	Stage 3

Let’s create a table of values. Let $n =$ stage number, and let $a_n =$ the number of matchsticks used in that stage. Then note the common difference.

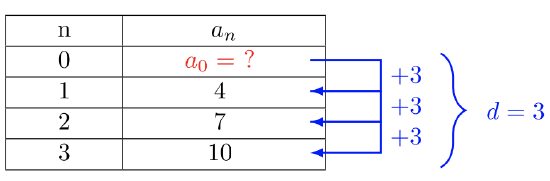
$clipboard_e25ba1d367972bd713a4ef5118c739484.png$

Find the value $a_0$:

$\begin{array} &a_0 + 3 &= 4 \\ a_0 + 3 − 3 &= 4 − 3 \\ a_0 &= 1 \end{array}$

The general term of the sequence is:

$a_n = 3n + 1$

Compute $a_{34}$ to find the number of matchsticks in stage $34$:

$a_{34} = 3(\textcolor{red}{34}) + 1 = 103$.

There are $103$ matchsticks in stage $34$.

What stage would require $220$ matchsticks? We are looking for the stage-number, given the number of matchsticks. Find $n$ if $a_n = 220$.

$\begin{array} &220 &= 3n + 1 \\ 219 &= 3n \\ 73 &= n \end{array}$

Answer Stage $73$ would require $220$ matchsticks.

Example 8.2.3

Cory buys $5$ items at the grocery store with prices $a_1$, $a_2$, $a_3$, $a_4$, $a_5$ which is an arithmetic sequence. The least expensive item is $$1.89$, while the total cost of the $5$ items is $$12.95$. What is the cost of each item?

Solution

Put the $5$ items in order of expense: least to most and left to right. Because it is an arithmetic sequence, each item is $d$ more dollars than the previous item. Each item’s price can be written in terms of the price of the least expensive item, $a_1$, and $a_1 = $1.89$.

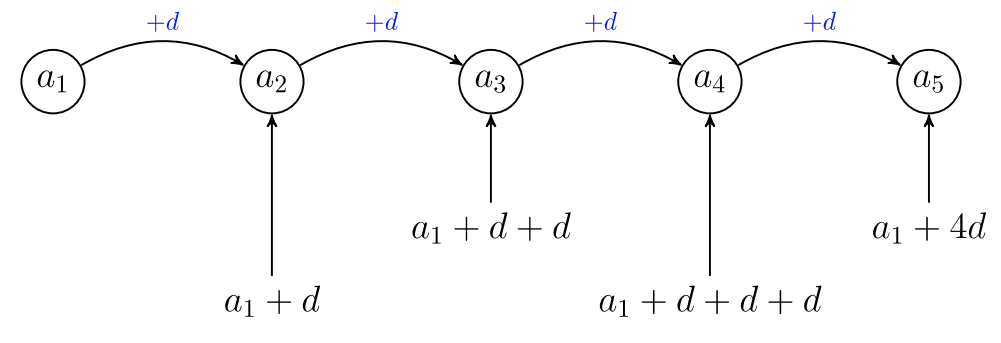
$clipboard_e4455aea24708d7e0d8b83d55c771a802.png$

The diagram above gives $5$ expressions for the costs of the $5$ items in terms of $a_1$ and the common difference is $d$.

$\begin{array} &a_1 + a_2 + a_3 + a_4 + a_5 &= 12.95 &\text{Total cost of \(5$ items is $$12.95$.} \\ a_1 + (a_1 + d) + (a_1 + 2d) + (a_1 + 3d) + (a_1 + 4d) &= 12.95 &\text{See diagram for substitutions.} \\ 5s_1 + 10d &= 12.95 &\text{Gather like terms.} \\ 5(1.89) + 10d &= 12.95 &a_1 = 1.89. \\ 9.45 + 10d &= 12.95 &\text{Simplify.} \\ 9.45 + 10d − 9.45 &= 12.95 − 9.45 &\text{Subtract $9.45$ from each side of equation.} \\ 10d &= 3.50 &\text{Simplify. Then divide both sides by $10$.} \\ d &= 0.35 &\text{The common difference is $$0.35$.} \end{array}\)

Now that we know the common difference, $d = $0.35$, we can answer the question.

$clipboard_e0e8f0221b97bd16399f771ecb8447115.png$

The price of each item is as follows: $$1.89, $2.24, $2.59, $2.94, $3.29$.

Try It! (Exercises)

1. ZKonnect cable company requires customers sign a $2$-year contract to use their services. The following describes the penalty for breaking contract: Your services are subject to a minimum term agreement of $24$ months. If the contract is terminated before the end of the $24$-month contract, an early termination fee is assessed in the following manner: $$230$ termination fee is assessed if contract is terminated in the first $30$ days of service. Thereafter, the termination fee decreases by $$10$ per month of contract.

If Jack enters contract with ZKonnect on April 1^st of $2021$, but terminates the service on January 10^th of $2022$, what are Jack’s early termination fees?
The general term $a_n$ describes the termination fees for the stated contract. Describe the meaning of the variable $n$ in the context of this problem. Find the general term $a_n$.
Is the early termination fee a finite sequence or an infinite sequence? Explain.
Find the value of $a_{13}$ and interpret its meaning in words.

2. A drug company has manufactured $4$ million doses of a vaccine to date. They promise additional production at a rate of $1.2$ million doses/month over the next year.

How many doses of the vaccine, in total, will have been produced after a year?
The general term $a_n$ describes the total number of doses of the vaccine produced. Describe the meaning of the variable $n$ in the context of this problem. Find the general term$a_n$.
Find the value of $a_8$ and interpret its meaning in words.

3. The theater shown at right has $22$ seats in the first row of the “A Center” section. Each row behind the first row gains two additional seats.

Let $a_n = 22 + 2n$, starting with $n = 0$. Give the first $10$ values of this sequence.
Using $a_n = 22 + 2n$, Find the value of $a_{10}$ and interpret its meaning in words in the context of this problem. Careful! Does $n=$ row number?
How many seats, in total, are in “A Center” section if there are $12$ rows in the section?

$clipboard_e155e2fcdec756f87a528b58fbd4f1e5d.png$

4) Logs are stacked in a pile with $48$ logs on the bottom row and $24$ on the top row. Each row decreases by three logs.

The stack, as described, has how many rows of logs?
Write the general term $a_n$ to describe the number of logs in a row in two different ways. Each general term should produce the same sequence, regardless of its starting $n$-value.

i. Start with $n = 0$.

ii. Start with $n = 1$.

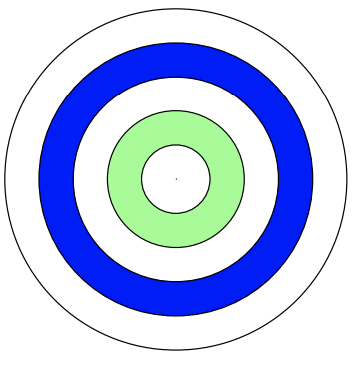
5) The radii of the target circle are an arithmetic sequence. If the area of the innermost circle is $\pi \text{un}^2$ and the area of the entire target is $49 \pi \text{un}^2$, what is the area of the blue ring? [The formula for area of a circle is $A = \pi r^2$].

$clipboard_e3624435db52cd10cbabe0c840da4a4b8.png$

6) Three stages of a pattern are shown below, using matchsticks. Each stage adds another triangle and requires a certain number of matchsticks. If we keep up the pattern…

How many matchsticks are required to make the figure in stage $34$?
What stage would require $325$ matchsticks?

$clipboard_e18c4290c686fe3b44e586ded85827bdf.png$	$clipboard_ec19b0ede179c5bd9a73db8dc18cc622b.png$	$clipboard_edf890e3bbdeef56b031c401c05c96ab3.png$
Stage 1	Stage 2	Stage 3

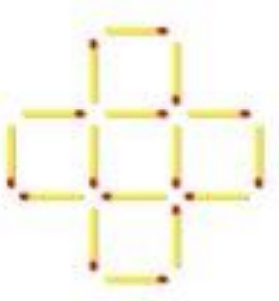
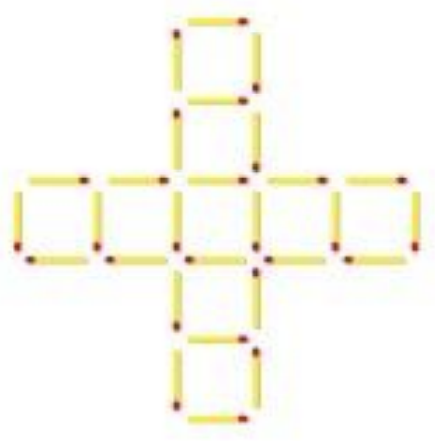
7) Three stages of a pattern are shown below, using matchsticks. Each stage requires a certain number of matchsticks. If we keep up the pattern…

How many matchsticks are required to make the figure in stage $22$?
What stage would require $424$ matchsticks?

$clipboard_e719f55232c125656cf9ed82e0ef1d0f2.png$	$clipboard_ef02b6ddba521a501b3d88c743adcff6c.png$	$clipboard_e818e430ba656d4b69074b6e78f7be84b.png$
Stage 1	Stage 2	Stage 3