1.1: Measuring Angles
- Page ID
- 37207
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Measuring Angles in Degrees
The two most common units for measuring angles are degrees and radians. Degrees are based on the ancient Mesopotamian assignment of $360^{\circ}$ to a complete circle. This has its origin in the division of the horizon of the nighttime sky as the earth takes 365 days to travel around the sun. Because degrees were originally developed by the Mesopotamians, they are often also broken out into 60 unit measures of minutes and seconds. Sixty seconds make one minute and sixty minutes makes one degree.
60 seconds \(=1\) minute or \(60^{\prime \prime}=1^{\prime}\)
60 minutes \(=1\) degree or \(60^{\prime}=1^{2}\)
Angles measured in degrees may also be expressed using decimal portions of a degree, for example:
\(72.5^{\circ}=72^{\circ} 30^{\prime}\)
Converting from decimal to DMS
Converting between degrees expressed with decimals and the degrees, minutes, seconds format (DMS) is relatively simple. If you're converting from degrees expressed with decimals to DMS, simply take the portion of the angle behind the decimal point and multiply by \(60 .\) In our previous example, we would take the .5 from \(72.5^{\circ}\) and multiply this by \(60: 0.5^{*} 60=30 .\) So, the angle in DMS units would be \(72^{\circ} 30^{\prime}\)
Examples
Convert \(21.85^{\circ}\) to DMS units
\(0.85 * 60=51\)
\(\mathrm{So}, 21.85^{\circ}=21^{\circ} 51^{\prime}\)
Convert \(143.27^{\text {to }}\) DMS units
\(0.27 * 60=16.2\)
So, \(143.27^{\circ}=143^{\circ} 16.2^{\prime}\)
In order to compute the number of seconds needed to express this angle in DMS units, we take the decimal portion of the minutes and multiply by 60:
\(0.2 * 60=12\)
So, \(143.27^{\circ}=143^{\circ} 16.2^{\prime}=143^{\circ} 16^{\prime} 12^{\prime \prime}\)
In the example above we ended with a whole number of seconds. If you don'tget a whole number for the seconds then you can leave the seconds with a decimal portion. For example, if you wanted to convert \(22.847^{\circ}\) to DMS units:
\(22.847^{\circ}=22^{\circ} 50.82^{\prime}=22^{\circ} 50^{\prime} 49.2^{\prime \prime}\)
Converting from DMS to decimal
To convert from DMS units to decimals, simply take the seconds portion and divide by 60 to make it a decimal:
\(129^{\circ} 19^{\prime} 30^{\prime \prime}=129^{\circ} 19.5^{\prime}\)
Then take the new minutes portion and divide it by 60
\(\frac{19.5}{60}=0.325\)
This is the decimal portion of the angle
\(129^{\circ} 19^{\prime} 30^{\prime \prime}=129^{\circ} 19.5^{\prime}=129.325^{\circ}\)
If you end up with repeating decimals in this process that's fine-just indicate the repeating portion with a bar.
Examples
Convert \(42^{\circ} .27^{\prime} 36^{\prime \prime}\) to decimal degrees
\(\frac{36}{60}=0.6\)
\(42^{\circ} \quad 27^{\prime} 36^{\prime \prime}=42^{\circ} \quad 27.6^{\prime}\)
\(\frac{27.6}{60}=0.46\)
\(42^{\circ} \quad 27.6^{\prime}=42.46^{\circ}\)
Convert \(17^{\circ} 40^{\prime} 18^{\prime \prime}\) to decimal degrees
\(\frac{18}{60}=0.3\)
\(17^{\circ} 40^{\prime} 18^{\prime \prime}=17^{\circ} 40.3^{\prime}\)
\(\frac{40.3}{60}=0.671 \overline{6}\)
\(17^{\circ} 40^{\prime} 18^{\prime \prime}=17^{\circ} 40.3^{\prime}=17.671 \overline{6}^{\circ}\)
Measuring Angles in Radians
The other most commonly used method for measuring angles is radian measure. Radian measure is based on the central angle of a circle. A given central angle will trace out an arc of a particular length on the circle. The ratio of the arc length to the radius of the circle is the angle measure in radians. The benefit of radian measure is that it is based on a ratio of distances whereas degree measure is not. This allows radians to be used in calculus in situations in which degree measure would be inappropriate.
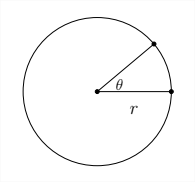
The length of the arc intersected by the central angle is the portion of the circumference swept out by the angle along the edge of the circle. The circumference of the circle would be \(2 \pi r,\) so the length of the arc would be \(\frac{\theta}{360^{\circ}} * 2 \pi r .\) The ratio of this arclength to the radius is \(\frac{\frac{\theta}{1000}+2 \pi r}{r}\) or
\[\frac{2 \pi}{360^{\circ}} * \theta\]
or in reduced form
\[\frac{\pi}{180^{\circ}} * \theta\]
This assumes that the angle has been expressed in degrees to begin with. If an angle is expressed in radian measure, then to convert it into degrees, simply multiply by \(\frac{180^{\circ}}{\pi}\)
Examples - Degrees to Radians
Convert \(60^{\circ}\) to radians
\(\frac{\pi}{180^{\circ}} * 60^{\circ}=\frac{\pi}{3}\)
Convert \(142^{\circ}\) to radians
\(\frac{\pi}{180^{\circ}} * 142^{\circ}=\frac{71 \pi}{90}\) or \(0.7 \overline{8} \pi\)
Examples - Radians to Degrees
Convert \(\frac{\pi}{10}\) to degrees
\(\frac{180^{\circ}}{\pi} * \frac{\pi}{10}=18^{\circ}\)
Convert \(\frac{\pi}{2}\) to degrees
\(\frac{180^{\circ}}{\pi} * \frac{\pi}{2}=90^{\circ}\)
Another way to convert radians to degrees is to simply replace the \(\pi\) with \(180^{\circ}:\)
\(\frac{\pi}{10}=\frac{180^{\circ}}{10}=18^{\circ}\)
\(\frac{\pi}{2}=\frac{180^{\circ}}{2}=90^{\circ}\)
Exercises 1.1 Convert each angle measure to decimal degrees.
\(3.91^{\circ} 50^{\prime}\)
1. \(27 \times 40\)
4 \(34 \%\)
\begin{tabular}{llllll}
7. & \(17^{\circ}\) & \(25^{\prime}\) & \(5 .\) & \(274^{\circ}\) & \(18^{\prime}\) & \(6 .\) & \(165^{\circ}\) & \(48^{\prime}\) \\
\hline
\end{tabular}
\(10 . \quad 141^{\circ} 6^{\prime} 9^{\prime \prime}\)
11. \(\quad 211^{\circ} 46^{\prime} 48^{\prime \prime}\)
\(12 . \quad 19^{\circ} 12^{\prime} 18^{\prime \prime}\)
Convert each angle measure to DMS notation. 13. \(31.425^{\circ}\)
\(14 . \quad 159.84^{\circ}\)
\(15 . \quad 6.78^{\circ}\)
\(\begin{array}{ll}16 . & 24.56^{\circ} \\ 19 . & 18.9^{\circ}\end{array}\)
\(17 . \quad 110.25^{\circ}\)
\(18 . \quad 64.16^{\circ}\)
\(\begin{array}{ll}19 . & 18.9^{\circ} \\ 22 . & 55.17^{\circ}\end{array}\)
\(20 . \quad 85.14^{\circ}\)
21. \(220.43^{\circ}\)
\(23.70 .214^{\circ}\)
\(24 . \quad 116.32^{\circ}\)
Convert each angle measure from degrees to radians.
\(25 . \quad 30^{\circ}\)
\(26 . \quad 120^{\circ}\)
\(27 . \quad 45^{\circ}\)
\(28 . \quad 225^{\circ}\)
\(29 . \quad 60^{\circ}\)
\(30 . \quad 150^{\circ}\)
\(31.90^{\circ}\)
\(32 . \quad 270^{\circ}\)
\(33 . \quad 15^{\circ}\)
\(34.36^{\circ}\)
\(35 . \quad 12^{\circ}\)
\(36 . \quad 104^{\circ}\)
Convert each angle measure from radians to degrees.
37
\(38 . \quad \frac{\pi}{5}\)
\(39 . \quad \frac{\pi}{3}\)
\(40 . \quad \frac{\pi}{6}\)
\(4^{7}\)
\(42 . \quad \frac{7 \pi}{3}\)
\(43 . \quad \frac{5 \pi}{2}\)
\(44 . \quad \frac{7 \pi}{4}\)
\(45 . \quad \frac{5 \pi}{6}\)
\(46 . \quad \frac{2 \pi}{3}\)
\(47 . \quad \pi\)
\(48 . \quad \frac{7 \pi}{2}\)


