7.2: Circles

Last updated
Save as PDF

Page ID: 80795

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Recall from Geometry that a circle can be determined by fixing a point (called the center) and a positive number (called the radius) as follows.

Definition 7.1

A circle with center $(h,k)$ and radius $r>0$ is the set of all points $(x, y)$ in the plane whose distance to $(h,k)$ is $r$.

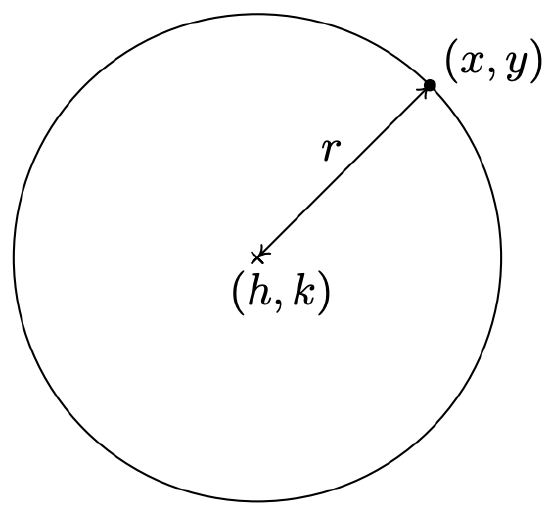
$Screen Shot 2022-04-21 at 4.38.42 PM.png$

From the picture, we see that a point $(x,y)$ is on the circle if and only if its distance to $(h,k)$ is $r$. We express this relationship algebraically using the Distance Formula, Equation 1.1, as \[r = \sqrt{(x - h)^2 + (y-k)^2}\nonumber\] By squaring both sides of this equation, we get an equivalent equation (since $r > 0$) which gives us the standard equation of a circle.

Equation 7.1. The Standard Equation of a Circle

The Standard Equation of a Circle: The equation of a circle with center $(h,k)$ and radius $r >0$ is $(x-h)^2 + (y-k)^2 = r^2.$

Example 7.2.1

Write the standard equation of the circle with center $(-2,3)$ and radius $5$.

Solution

Here, $(h,k) = (-2,3)$ and $r = 5$, so we get

\[\begin{array}{rcl} (x-(-2))^2+(y-3)^2 &= &(5)^2 \\ (x+2)^2+(y-3)^2 & = & 25 \end{array}\nonumber\]

Example 7.2.2

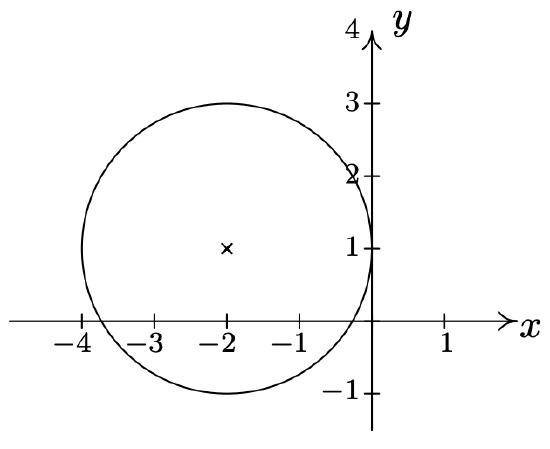
Graph $(x+2)^2+(y-1)^2 = 4$. Find the center and radius.

Solution

From the standard form of a circle, Equation 7.1, we have that $x + 2$ is $x-h$, so $h = -2$ and $y - 1$ is $y - k$ so $k = 1$. This tells us that our center is $(-2,1)$. Furthermore, $r^2 = 4$, so $r = 2$. Thus we have a circle centered at $(-2,1)$ with a radius of $2$. Graphing gives us

$Screen Shot 2022-04-21 at 4.58.21 PM.png$

If we were to expand the equation in the previous example and gather up like terms, instead of the easily recognizable $(x+2)^2 + (y-1)^2 = 4$, we’d be contending with $x^2 + 4x + y^2 - 2y + 1 = 0.$ If we’re given such an equation, we can complete the square in each of the variables to see if it fits the form given in Equation 7.1 by following the steps given below.

To Write the Equation of a Circle in Standard Form

Group the same variables together on one side of the equation and position the constant on the other side.
Complete the square on both variables as needed.
Divide both sides by the coefficient of the squares. (For circles, they will be the same.)

Example 7.2.3

Complete the square to find the center and radius of $3x^2 - 6x + 3y^2 + 4y -4 = 0$.

Solution.

\[\begin{array}{rclr} 3x^2 - 6x + 3y^2 + 4y -4 & = & 0 & \\ 3x^2 - 6x + 3y^2 + 4y & = & 4 & \mbox{add $4$ to both sides} \\[4pt] 3\left(x^2 - 2x \right) + 3\left(y^2 + \dfrac{4}{3} y\right) & = & 4 & \mbox{factor out leading coefficients} \\ [10pt] 3\left(x^2 - 2x + \underline{1} \right) + 3\left(y^2 + \dfrac{4}{3} y + \underline{\underline{\dfrac{4}{9}}} \right) & = & 4 + 3\underline{(1)} + 3\underline{\underline{\left(\dfrac{4}{9}\right)}} & \mbox{complete the square in $x$, $y$} \\ [10pt] 3(x - 1)^2 + 3\left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{3} & \mbox{factor} \\ [10pt] (x - 1)^2 + \left(y + \dfrac{2}{3}\right)^2 & = & \dfrac{25}{9} & \mbox{divide both sides by $3$}\end{array}\nonumber\]

From Equation 7.1, we identify $x - 1$ as $x - h$, so $h = 1$, and $y + \frac{2}{3}$ as $y - k$, so $k = - \frac{2}{3}$. Hence, the center is $(h,k) = \left(1, -\frac{2}{3}\right)$. Furthermore, we see that $r^2 = \frac{25}{9}$ so the radius is $r = \frac{5}{3}$.

It is possible to obtain equations like $(x-3)^2 + (y+1)^2 = 0$ or $(x-3)^2 + (y+1)^2 = -1$, neither of which describes a circle. (Do you see why not?) The reader is encouraged to think about what, if any, points lie on the graphs of these two equations. The next example uses the Midpoint Formula, Equation 1.2, in conjunction with the ideas presented so far in this section.

Example 7.2.4

Write the standard equation of the circle which has $(-1,3)$ and $(2,4)$ as the endpoints of a diameter.

We recall that a diameter of a circle is a line segment containing the center and two points on the circle. Plotting the given data yields

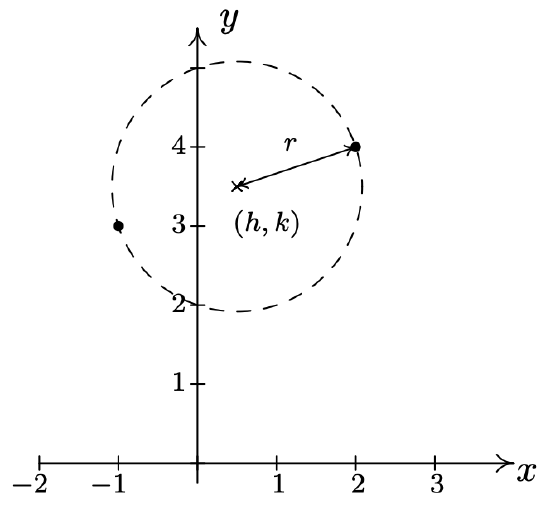
$Screen Shot 2022-04-21 at 5.18.12 PM.png$

Since the given points are endpoints of a diameter, we know their midpoint $(h, k)$ is the center of the circle. Equation 1.2 gives us

\[\begin{array}{rcl} (h,k) & = & \left( \dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2} \right) \\ [8pt] & = & \left( \dfrac{-1+2}{2}, \dfrac{3+4}{2} \right) \\ [8pt] & = & \left( \dfrac{1}{2}, \dfrac{7}{2} \right) \end{array}\nonumber\]

The diameter of the circle is the distance between the given points, so we know that half of the distance is the radius. Thus,

\[\begin{array}{rcl} r & = & \dfrac{1}{2} \sqrt{\left(x_2 - x_1\right)^2+\left(y_2-y_1\right)^2} \\ [8pt] & = & \dfrac{1}{2} \sqrt{(2-(-1))^2+(4-3)^2} \\ [8pt] & = & \dfrac{1}{2} \sqrt{3^2+1^2} \\ [8pt] & = &\dfrac{\sqrt{10}}{2} \end{array}\nonumber\]

Finally, since $\left( \dfrac{\sqrt{10}}{2} \right)^2 = \dfrac{10}{4}$, our answer becomes $\left(x - \dfrac{1}{2} \right)^2 + \left(y - \dfrac{7}{2} \right)^2 =\dfrac{10}{4}$

We close this section with the most important¹ circle in all of mathematics: the Unit Circle.

Definition 7.2

The Unit Circle is the circle centered at $(0,0)$ with a radius of $1$. The standard equation of the Unit Circle is $x^2 + y^2 = 1.$

Example 7.2.5

Find the points on the unit circle with $y$-coordinate $\dfrac{\sqrt{3}}{2}$.

Solution

We replace $y$ with $\dfrac{\sqrt{3}}{2}$ in the equation $x^2 + y^2 = 1$ to get

\[\begin{array}{rcl} x^2 + y^2 & = & 1 \\ x^2 + \left(\dfrac{\sqrt{3}}{2}\right)^2 & = & 1 \\ [13pt] \dfrac{3}{4} + x^2 & = & 1 \\ x^2 & = & \dfrac{1}{4} \\ x & = & \pm \sqrt{\dfrac{1}{4}} \\ [7pt] x & = & \pm \dfrac{1}{2} \end{array}\nonumber\]

Our final answers are $\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)$ and $\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2} \right)$.

7.2.1. Exercises

In Exercises 1 - 6, find the standard equation of the circle and then graph it.

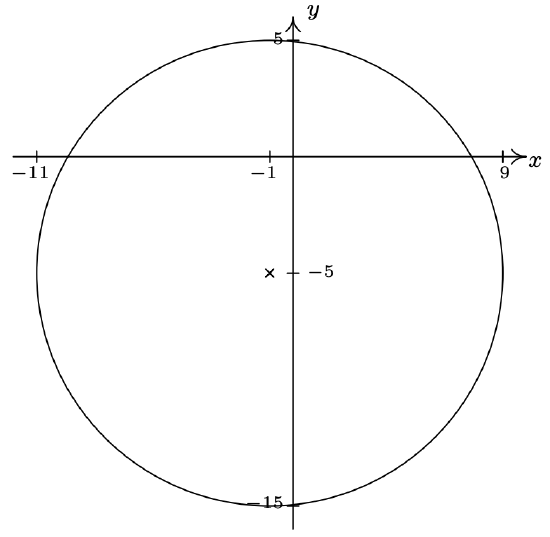
Center $(-1, -5)$, radius $10$
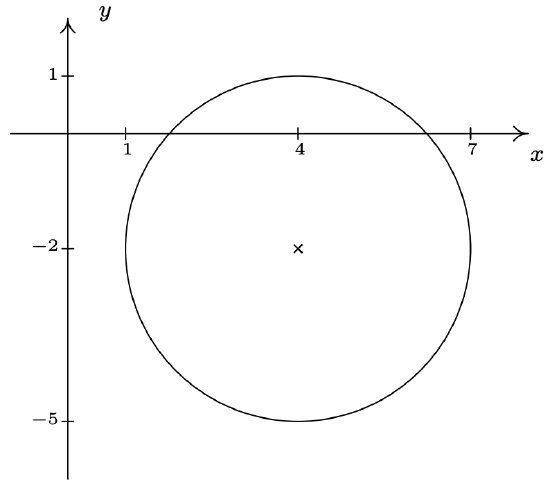
Center $(4,-2)$, radius $3$
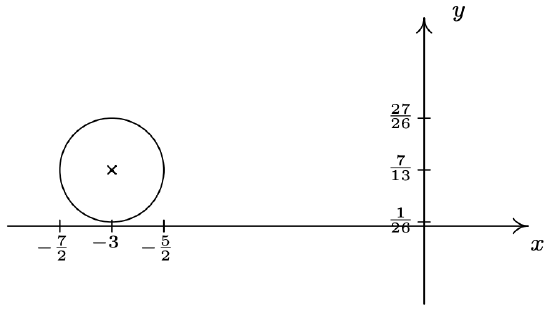
Center $\left(-3, \frac{7}{13}\right)$, radius $\frac{1}{2}$
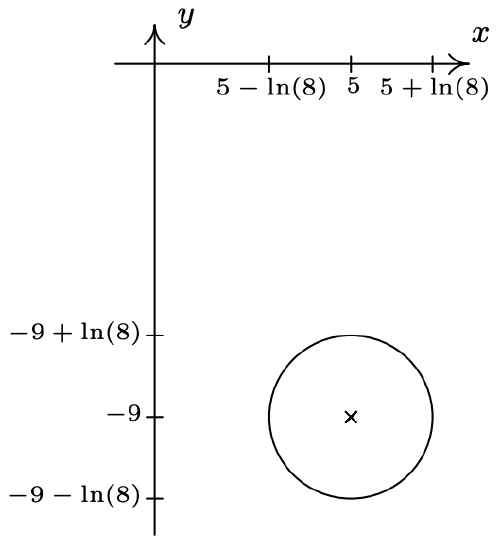
Center $(5, -9)$, radius $\ln(8)$
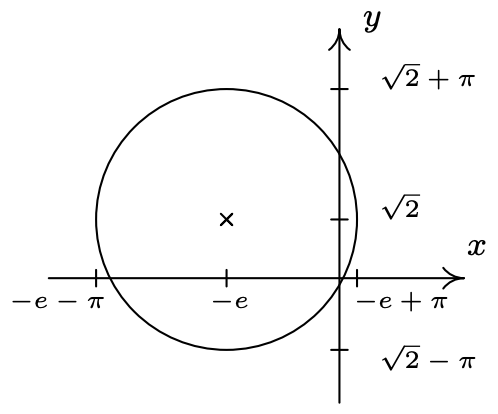
Center $\left(-e, \sqrt{2}\right)$, radius $\pi$
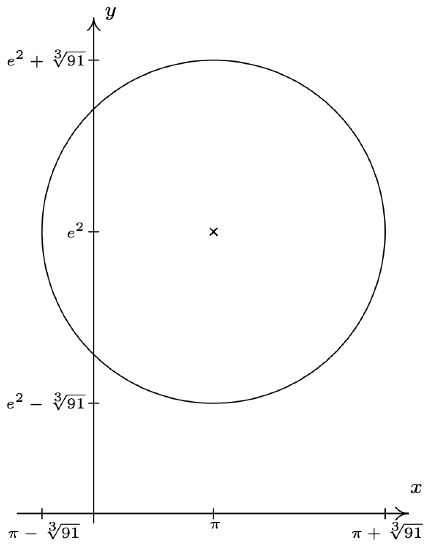
Center $(\pi, e^{2})$, radius $\sqrt[3]{91}$

In Exercises 7 - 12, complete the square in order to put the equation into standard form. Identify the center and the radius or explain why the equation does not represent a circle.

$x^{2} - 4x + y^{2} + 10y = -25$
$-2x^{2} - 36x - 2y^{2} - 112 = 0$
$x^2+y^2+8x-10y -1 =0$
$x^2+y^2+5x-y-1=0$
$4x^{2} + 4y^{2} - 24y + 36 = 0$
$x^{2} + x + y^{2} - \frac{6}{5}y = 1$

In Exercises 13 - 16, find the standard equation of the circle which satisfies the given criteria.

center $(3, 5)$, passes through $(-1, -2)$
center $(3, 6)$, passes through $(-1, 4)$
endpoints of a diameter: $(3,6)$ and $(-1,4)$
endpoints of a diameter: $\left( \frac{1}{2}, 4\right)$, $\left(\frac{3}{2}, -1\right)$
The Giant Wheel at Cedar Point is a circle with diameter 128 feet which sits on an 8 foot tall platform making its overall height is 136 feet.² Find an equation for the wheel assuming that its center lies on the $y$-axis and that the ground is the $x$-axis.
Verify that the following points lie on the Unit Circle: $(\pm 1, 0)$, $(0, \pm 1)$, $\left(\pm \frac{\sqrt{2}}{2}, \pm \frac{\sqrt{2}}{2}\right)$, $\left(\pm \frac{1}{2}, \pm \frac{\sqrt{3}}{2}\right)$ and $\left(\pm \frac{\sqrt{3}}{2}, \pm \frac{1}{2}\right)$
Discuss with your classmates how to obtain the standard equation of a circle, Equation 7.1, from the equation of the Unit Circle, $x^2+y^2=1$ using the transformations discussed in Section 1.7. (Thus every circle is just a few transformations away from the Unit Circle.)
Find an equation for the function represented graphically by the top half of the Unit Circle. Explain how the transformations is Section 1.7 can be used to produce a function whose graph is either the top or bottom of an arbitrary circle.
Find a one-to-one function whose graph is half of a circle. (Hint: Think piecewise.)

7.2.2. Answers

$(x + 1)^{2} + (y + 5)^{2} = 100$
$Screen Shot 2022-04-28 at 3.12.27 PM.png$
$(x-4)^2+(y+2)^2 = 9$
$Screen Shot 2022-04-28 at 3.13.04 PM.png$
$\left(x + 3\right)^{2} + \left(y - \frac{7}{13}\right)^{2} = \frac{1}{4}$
$Screen Shot 2022-04-28 at 3.14.31 PM.png$
$(x - 5)^{2} + (y + 9)^{2} = (\ln(8))^{2}$
$Screen Shot 2022-04-28 at 3.16.15 PM.png$
$(x + e)^{2} + \left(y - \sqrt{2} \right)^{2} = \pi^{2}$
$Screen Shot 2022-04-28 at 3.16.48 PM.png$
$\left(x - \pi \right)^{2} + \left(y - e^{2}\right)^{2} = 91^{\frac{2}{3}}$
$Screen Shot 2022-04-28 at 3.17.19 PM.png$
$(x - 2)^{2} + (y + 5)^{2} = 4$
Center $(2, -5)$, radius $r = 2$
$(x + 9)^{2} + y^{2} = 25$
Center $(-9, 0)$, radius $r = 5$
$(x+4)^2 + (y-5)^2 = 42$
Center $(-4,5)$, radius $r = \sqrt{42}$
$\left(x + \frac{5}{2}\right)^2 + \left(y - \frac{1}{2}\right)^2 = \frac{30}{4}$
Center $\left( -\frac{5}{2}, \frac{1}{2}\right)$, radius $r = \frac{\sqrt{30}}{2}$
$x^{2} + (y - 3)^{2} = 0$
This is not a circle.
$\left(x + \frac{1}{2}\right)^{2} + \left(y - \frac{3}{5}\right)^{2} = \frac{161}{100}$
Center $\left(-\frac{1}{2}, \frac{3}{5}\right)$, radius $r = \frac{\sqrt{161}}{10}$
$(x - 3)^{2} + (y - 5)^{2} = 65$
$(x-3)^2+(y-6)^2 = 20$
$(x-1)^2 + (y-5)^2 = 5$
$(x-1)^2 + \left(y - \frac{3}{2}\right)^2 = \frac{13}{2}$
$x^{2} + (y - 72)^{2} = 4096$