10.4: Trigonometric Identities

In Section 10.3, we saw the utility of the Pythagorean Identities in Theorem 10.8 along with the Quotient and Reciprocal Identities in Theorem 10.6. Not only did these identities help us compute the values of the circular functions for angles, they were also useful in simplifying expressions involving the circular functions. In this section, we introduce several collections of identities which have uses in this course and beyond. Our first set of identities is the ‘Even / Odd’ identities.¹

Theorem 10.12. Even / Odd Identities

For all applicable angles $\theta$,

• $\cos(-\theta) = \cos(\theta)$
• $\sec(-\theta) = \sec(\theta)$
• $\sin(-\theta) = -\sin(\theta)$
• $\csc(-\theta) = -\csc(\theta)$
• $\tan(-\theta) = -\tan(\theta)$
• $\cot(-\theta) = -\cot(\theta)$

In light of the Quotient and Reciprocal Identities, Theorem 10.6, it suffices to show $\cos(-\theta) = \cos(\theta)$ and $\sin(-\theta) = -\sin(\theta)$. The remaining four circular functions can be expressed in terms of $\cos(\theta)$ and $\sin(\theta)$ so the proofs of their Even / Odd Identities are left as exercises. Consider an angle $\theta$ plotted in standard position. Let $\theta_0$ be the angle coterminal with $\theta$ with $0 \leq \theta_0 < 2\pi$. (We can construct the angle $\theta_0$ by rotating counter-clockwise from the positive $x$-axis to the terminal side of $\theta$ as pictured below.) Since $\theta$ and $\theta_0$ are coterminal, $\cos(\theta) = \cos(\theta_0)$ and $\sin(\theta) = \sin(\theta_0)$.

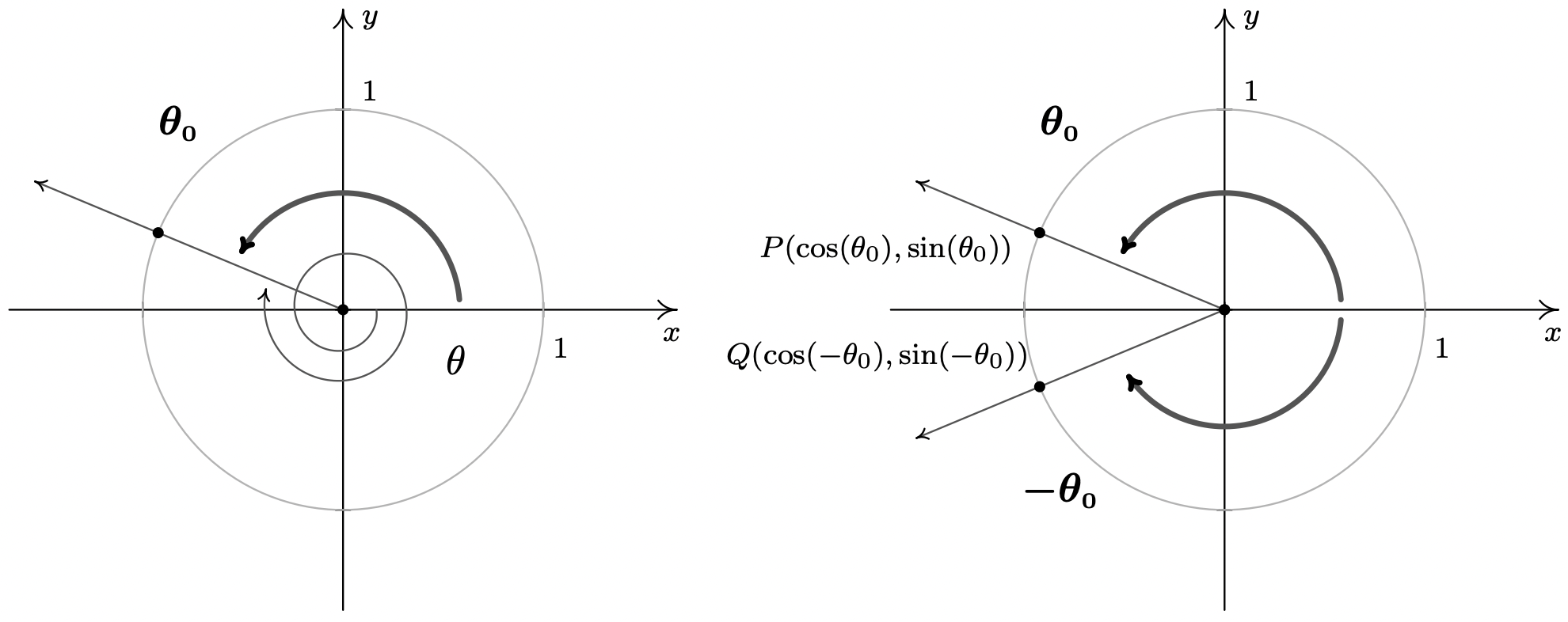
We now consider the angles $-\theta$ and $-\theta_0$. Since $\theta$ is coterminal with $\theta_0$, there is some integer $k$ so that $\theta = \theta_0 + 2\pi \cdot k$. Therefore, $-\theta = -\theta_0 - 2\pi \cdot k = -\theta_0 + 2\pi \cdot(-k)$. Since $k$ is an integer, so is $(-k)$, which means $-\theta$ is coterminal with $-\theta_0$. Hence, $\cos(-\theta) = \cos(-\theta_0)$ and $\sin(-\theta) = \sin(-\theta_0)$. Let $P$ and $Q$ denote the points on the terminal sides of $\theta_0$ and $-\theta_0$, respectively, which lie on the Unit Circle. By definition, the coordinates of $P$ are $(\cos(\theta_0),\sin(\theta_0))$ and the coordinates of $Q$ are $(\cos(-\theta_0),\sin(-\theta_0))$. Since $\theta_0$ and $-\theta_0$ sweep out congruent central sectors of the Unit Circle, it follows that the points $P$ and $Q$ are symmetric about the $x$-axis. Thus, $\cos(-\theta_0) = \cos(\theta_0)$ and $\sin(-\theta_0) = -\sin(\theta_0)$. Since the cosines and sines of $\theta_0$ and $-\theta_0$ are the same as those for $\theta$ and $-\theta$, respectively, we get $\cos(-\theta) = \cos(\theta)$ and $\sin(-\theta) = -\sin(\theta)$, as required. The Even / Odd Identities are readily demonstrated using any of the ‘common angles’ noted in Section 10.2. Their true utility, however, lies not in computation, but in simplifying expressions involving the circular functions. In fact, our next batch of identities makes heavy use of the Even / Odd Identities.

Theorem 10.13. Sum and Difference Identities for Cosine

For all angles $\alpha$ and $\beta$,

• $\cos(\alpha + \beta) = \cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)$
• $\cos(\alpha - \beta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)$

We first prove the result for differences. As in the proof of the Even / Odd Identities, we can reduce the proof for general angles $\alpha$ and $\beta$ to angles $\alpha_0$ and $\beta_0$, coterminal with $\alpha$ and $\beta$, respectively, each of which measure between $0$ and $2\pi$ radians. Since $\alpha$ and $\alpha_0$ are coterminal, as are $\beta$ and $\beta_0$, it follows that $\alpha - \beta$ is coterminal with $\alpha_0 - \beta_0$. Consider the case below where $\alpha_0 \geq \beta_0$.

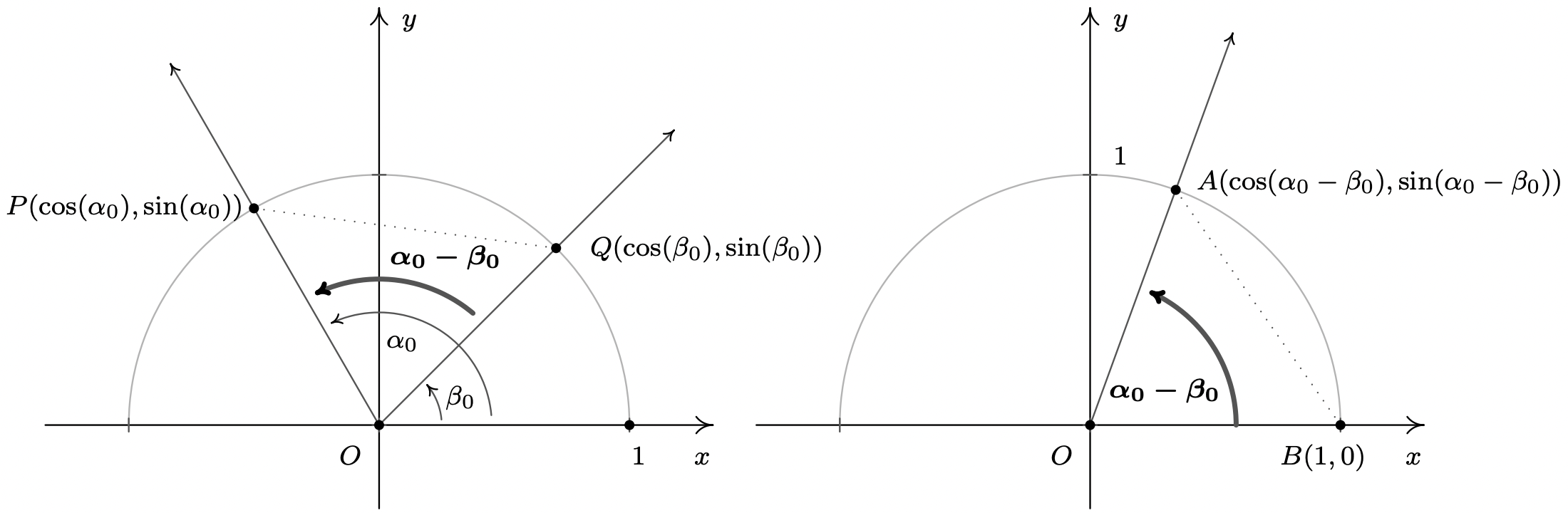
Since the angles $POQ$ and $AOB$ are congruent, the distance between $P$ and $Q$ is equal to the distance between $A$ and $B$.² The distance formula, Equation 1.1, yields

$$\sqrt{\left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}}=\sqrt{\left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2}}\nonumber$$

Squaring both sides, we expand the left hand side of this equation as

$$\begin{aligned} \left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}=& \cos ^{2}\left(\alpha_{0}\right)-2 \cos \left(\alpha_{0}\right) \cos \left(\beta_{0}\right)+\cos ^{2}\left(\beta_{0}\right) \\ &+\sin ^{2}\left(\alpha_{0}\right)-2 \sin \left(\alpha_{0}\right) \sin \left(\beta_{0}\right)+\sin ^{2}\left(\beta_{0}\right) \\ =& \cos ^{2}\left(\alpha_{0}\right)+\sin ^{2}\left(\alpha_{0}\right)+\cos ^{2}\left(\beta_{0}\right)+\sin ^{2}\left(\beta_{0}\right) \\ &-2 \cos \left(\alpha_{0}\right) \cos \left(\beta_{0}\right)-2 \sin \left(\alpha_{0}\right) \sin \left(\beta_{0}\right) \end{aligned}\nonumber$$

From the Pythagorean Identities, $\cos^2(\alpha_0) + \sin^2(\alpha_0) = 1$ and $\cos^2(\beta_0) + \sin^2(\beta_0) = 1$, so

$$\left(\cos \left(\alpha_{0}\right)-\cos \left(\beta_{0}\right)\right)^{2}+\left(\sin \left(\alpha_{0}\right)-\sin \left(\beta_{0}\right)\right)^{2}=2-2 \cos \left(\alpha_{0}\right) \cos \left(\beta_{0}\right)-2 \sin \left(\alpha_{0}\right) \sin \left(\beta_{0}\right)\nonumber$$

Turning our attention to the right hand side of our equation, we find

$$\begin{aligned} \left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2} &=\cos ^{2}\left(\alpha_{0}-\beta_{0}\right)-2 \cos \left(\alpha_{0}-\beta_{0}\right)+1+\sin ^{2}\left(\alpha_{0}-\beta_{0}\right) \\ &=1+\cos ^{2}\left(\alpha_{0}-\beta_{0}\right)+\sin ^{2}\left(\alpha_{0}-\beta_{0}\right)-2 \cos \left(\alpha_{0}-\beta_{0}\right) \end{aligned}\nonumber$$

Once again, we simplify $\cos^2(\alpha_0 - \beta_0) + \sin^2(\alpha_0 - \beta_0)= 1$, so that

$$\left(\cos \left(\alpha_{0}-\beta_{0}\right)-1\right)^{2}+\left(\sin \left(\alpha_{0}-\beta_{0}\right)-0\right)^{2}=2-2 \cos \left(\alpha_{0}-\beta_{0}\right)\nonumber$$

Putting it all together, we get $2 - 2\cos(\alpha_0)\cos(\beta_0) - 2\sin(\alpha_0)\sin(\beta_0) = 2 - 2\cos(\alpha_0 - \beta_0)$, which simplifies to: $\cos(\alpha_0 - \beta_0) = \cos(\alpha_0)\cos(\beta_0) + \sin(\alpha_0)\sin(\beta_0)$. Since $\alpha$ and $\alpha_0$, $\beta$ and $\beta_0$ and $\alpha - \beta$ and $\alpha_0- \beta_0$ are all coterminal pairs of angles, we have $\cos(\alpha - \beta) = \cos(\alpha) \cos(\beta) + \sin(\alpha) \sin(\beta)$. For the case where $\alpha_0 \leq \beta_0$, we can apply the above argument to the angle $\beta_0 - \alpha_0$ to obtain the identity $\cos(\beta_0 - \alpha_0) = \cos(\beta_0)\cos(\alpha_0) + \sin(\beta_0)\sin(\alpha_0)$. Applying the Even Identity of cosine, we get $\cos(\beta_0 - \alpha_0) = \cos( - (\alpha_0 - \beta_0)) = \cos(\alpha_0 - \beta_0)$, and we get the identity in this case, too.

To get the sum identity for cosine, we use the difference formula along with the Even/Odd Identities

$$\cos (\alpha+\beta)=\cos (\alpha-(-\beta))=\cos (\alpha) \cos (-\beta)+\sin (\alpha) \sin (-\beta)=\cos (\alpha) \cos (\beta)-\sin (\alpha) \sin (\beta)\nonumber$$

We put these newfound identities to good use in the following example.

Example 10.4.1

1. Find the exact value of $\cos\left(15^{\circ}\right)$.
2. Verify the identity: $\cos\left(\frac{\pi}{2} - \theta\right) = \sin(\theta)$.

Solution

1. In order to use Theorem 10.13 to find $\cos\left(15^{\circ}\right)$, we need to write $15^{\circ}$ as a sum or difference of angles whose cosines and sines we know. One way to do so is to write $15^{\circ} = 45^{\circ} - 30^{\circ}$.

   $$\begin{array}{rcl} \cos\left(15^{\circ}\right) & = & \cos\left(45^{\circ} - 30^{\circ} \right) \\[4pt] & = & \cos\left(45^{\circ}\right)\cos\left(30^{\circ} \right) + \sin\left(45^{\circ}\right)\sin\left(30^{\circ} \right) \\[4pt] & = & \left( \dfrac{\sqrt{2}}{2} \right)\left( \dfrac{\sqrt{3}}{2} \right) + \left( \dfrac{\sqrt{2}}{2} \right)\left( \dfrac{1}{2} \right)\\[15pt] & = & \dfrac{\sqrt{6}+ \sqrt{2}}{4} \\ \end{array}\nonumber$$

2. In a straightforward application of Theorem 10.13, we find

   $$\begin{array}{rcl} \cos\left(\dfrac{\pi}{2} - \theta\right) & = & \cos\left(\dfrac{\pi}{2}\right)\cos\left(\theta\right) + \sin\left(\dfrac{\pi}{2}\right)\sin\left(\theta \right) \\ [10pt] & = & \left( 0 \right)\left( \cos(\theta) \right) + \left( 1 \right)\left( \sin(\theta) \right) \\ [4pt] & = & \sin(\theta) \\ \end{array}\nonumber$$

The identity verified in Example 10.4.1, namely, $\cos\left(\frac{\pi}{2} - \theta\right) = \sin(\theta)$, is the first of the celebrated ‘cofunction’ identities. These identities were first hinted at in Exercise 74 in Section 10.2. From $\sin(\theta) = \cos\left(\frac{\pi}{2} - \theta\right)$, we get:

$$\sin\left(\dfrac{\pi}{2} - \theta\right) = \cos\left(\dfrac{\pi}{2} -\left[\dfrac{\pi}{2} - \theta\right]\right) = \cos(\theta),\nonumber$$

which says, in words, that the ‘co’sine of an angle is the sine of its ‘co’mplement. Now that these identities have been established for cosine and sine, the remaining circular functions follow suit. The remaining proofs are left as exercises.

Theorem 10.14. Cofunction Identities

For all applicable angles $\theta$,

• $\cos\left(\dfrac{\pi}{2} - \theta \right) = \sin(\theta)$
• $\sin\left(\dfrac{\pi}{2} - \theta \right) = \cos(\theta)$
• $\sec\left(\dfrac{\pi}{2} - \theta \right) = \csc(\theta)$
• $\csc\left(\dfrac{\pi}{2} - \theta \right) = \sec(\theta)$
• $\tan\left(\dfrac{\pi}{2} - \theta \right) = \cot(\theta)$
• $\cot\left(\dfrac{\pi}{2} - \theta \right) = \tan(\theta)$

With the Cofunction Identities in place, we are now in the position to derive the sum and difference formulas for sine. To derive the sum formula for sine, we convert to cosines using a cofunction identity, then expand using the difference formula for cosine

$$\begin{array}{rcl} \sin(\alpha + \beta) & = & \cos\left( \dfrac{\pi}{2} - (\alpha + \beta) \right) \\ [10pt] & = & \cos\left( \left[\dfrac{\pi}{2} - \alpha \right] - \beta \right) \\ [10pt] & = & \cos\left(\dfrac{\pi}{2} - \alpha \right) \cos(\beta) + \sin\left(\dfrac{\pi}{2} - \alpha \right)\sin(\beta) \\ [10pt] & = & \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta) \\ \end{array}\nonumber$$

We can derive the difference formula for sine by rewriting $\sin(\alpha - \beta)$ as $\sin(\alpha + (-\beta))$ and using the sum formula and the Even / Odd Identities. Again, we leave the details to the reader.

Theorem 10.15. Sum and Difference Identities for Sine

For all angles $\alpha$ and $\beta$,

• $\sin(\alpha + \beta) = \sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)$
• $\sin(\alpha - \beta) = \sin(\alpha) \cos(\beta) - \cos(\alpha) \sin(\beta)$

Example 10.4.2

1. Find the exact value of $\sin\left(\frac{19 \pi}{12}\right)$
2. If $\alpha$ is a Quadrant II angle with $\sin(\alpha) = \frac{5}{13}$, and $\beta$ is a Quadrant III angle with $\tan(\beta) = 2$, find $\sin(\alpha - \beta)$.
3. Derive a formula for $\tan(\alpha + \beta)$ in terms of $\tan(\alpha)$ and $\tan(\beta)$.

Solution.

1. As in Example 10.4.1, we need to write the angle $\frac{19 \pi}{12}$ as a sum or difference of common angles. The denominator of $12$ suggests a combination of angles with denominators $3$ and $4$. One such combination is $\; \frac{19 \pi}{12} = \frac{4 \pi}{3} + \frac{\pi}{4}$. Applying Theorem 10.15, we get

   $$\begin{array}{rcl} \sin\left(\dfrac{19 \pi}{12}\right) & = & \sin\left(\dfrac{4 \pi}{3} + \dfrac{\pi}{4} \right) \\ [10pt] & = & \sin\left(\dfrac{4 \pi}{3} \right)\cos\left(\dfrac{\pi}{4} \right) + \cos\left(\dfrac{4 \pi}{3} \right)\sin\left(\dfrac{\pi}{4} \right) \\ [10pt] & = & \left( -\dfrac{\sqrt{3}}{2} \right)\left( \dfrac{\sqrt{2}}{2} \right) + \left( -\dfrac{1}{2} \right)\left( \dfrac{\sqrt{2}}{2} \right) \\[15pt] & = & \dfrac{-\sqrt{6}- \sqrt{2}}{4} \\ \end{array}\nonumber$$

2. In order to find $\sin(\alpha - \beta)$ using Theorem 10.15, we need to find $\cos(\alpha)$ and both $\cos(\beta)$ and $\sin(\beta)$. To find $\cos(\alpha)$, we use the Pythagorean Identity $\cos^2(\alpha) + \sin^2(\alpha) = 1$. Since $\sin(\alpha) = \frac{5}{13}$, we have $\cos^{2}(\alpha) + \left(\frac{5}{13}\right)^2 = 1$, or $\cos(\alpha) = \pm \frac{12}{13}$. Since $\alpha$ is a Quadrant II angle, $\cos(\alpha) = -\frac{12}{13}$. We now set about finding $\cos(\beta)$ and $\sin(\beta)$. We have several ways to proceed, but the Pythagorean Identity $1 + \tan^{2}(\beta) = \sec^{2}(\beta)$ is a quick way to get $\sec(\beta)$, and hence, $\cos(\beta)$. With $\tan(\beta) = 2$, we get $1 + 2^2 = \sec^{2}(\beta)$ so that $\sec(\beta) = \pm \sqrt{5}$. Since $\beta$ is a Quadrant III angle, we choose $\sec(\beta) = -\sqrt{5}$ so $\cos(\beta) = \frac{1}{\sec(\beta)} = \frac{1}{-\sqrt{5}} = -\frac{\sqrt{5}}{5}$. We now need to determine $\sin(\beta)$. We could use The Pythagorean Identity $\cos^{2}(\beta) + \sin^{2}(\beta) = 1$, but we opt instead to use a quotient identity. From $\tan(\beta) = \frac{\sin(\beta)}{\cos(\beta)}$, we have $\sin(\beta) = \tan(\beta) \cos(\beta)$ so we get $\sin(\beta) = (2) \left( -\frac{\sqrt{5}}{5}\right) = - \frac{2 \sqrt{5}}{5}$. We now have all the pieces needed to find $\sin(\alpha - \beta)$:

   $$\begin{array}{rcl} \sin(\alpha - \beta) & = & \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) \\ & = & \left( \dfrac{5}{13} \right)\left( -\dfrac{\sqrt{5}}{5} \right) - \left( -\dfrac{12}{13} \right)\left( - \dfrac{2 \sqrt{5}}{5} \right) \\ & = & -\dfrac{29\sqrt{5}}{65} \\ \end{array}\nonumber$$

3. We can start expanding $\tan(\alpha + \beta)$ using a quotient identity and our sum formulas

   $$\begin{array}{rcl} \tan(\alpha + \beta) & = & \dfrac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} \\ [10pt] & = & \dfrac{\sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)} \\ \end{array}\nonumber$$

   Since $\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}$ and $\tan(\beta) = \frac{\sin(\beta)}{\cos(\beta)}$, it looks as though if we divide both numerator and denominator by $\cos(\alpha) \cos(\beta)$ we will have what we want

   $$\begin{array}{rcl} \tan(\alpha + \beta) & = & \dfrac{\sin(\alpha) \cos(\beta) + \cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta) - \sin(\alpha) \sin(\beta)} \cdot\dfrac{\dfrac{1}{\cos(\alpha) \cos(\beta)}}{\dfrac{1}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\dfrac{\sin(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} + \dfrac{\cos(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}{\dfrac{\cos(\alpha) \cos(\beta)}{\cos(\alpha) \cos(\beta)} - \dfrac{\sin(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\dfrac{\sin(\alpha) \cancel{\cos(\beta)}}{\cos(\alpha) \cancel{\cos(\beta)}} + \dfrac{\cancel{\cos(\alpha)} \sin(\beta)}{\cancel{\cos(\alpha)} \cos(\beta)}}{\dfrac{\cancel{\cos(\alpha)} \cancel{\cos(\beta)}}{\cancel{\cos(\alpha)} \cancel{\cos(\beta)}} - \dfrac{\sin(\alpha) \sin(\beta)}{\cos(\alpha) \cos(\beta)}}\\ & & \\ & = & \dfrac{\tan(\alpha) + \tan(\beta)}{1 -\tan(\alpha) \tan(\beta)}\\ \end{array}\nonumber$$

   Naturally, this formula is limited to those cases where all of the tangents are defined.

The formula developed in Exercise 10.4.2 for $\tan(\alpha + \beta)$ can be used to find a formula for $\tan(\alpha - \beta)$ by rewriting the difference as a sum, $\tan(\alpha + (-\beta))$, and the reader is encouraged to fill in the details. Below we summarize all of the sum and difference formulas for cosine, sine and tangent.

Theorem 10.16. Sum and Difference Identities

For all applicable angles $\alpha$ and $\beta$,

• $\cos(\alpha \pm \beta) = \cos(\alpha) \cos(\beta) \mp \sin(\alpha) \sin(\beta)$
• $\sin(\alpha \pm \beta) = \sin(\alpha) \cos(\beta) \pm \cos(\alpha) \sin(\beta)$
• $\tan(\alpha \pm \beta) = \dfrac{\tan(\alpha) \pm \tan(\beta)}{1 \mp \tan(\alpha) \tan(\beta)}$

In the statement of Theorem 10.16, we have combined the cases for the sum ‘$+$’ and difference ‘$-$’ of angles into one formula. The convention here is that if you want the formula for the sum ‘$+$’ of two angles, you use the top sign in the formula; for the difference, ‘$-$’, use the bottom sign. For example, $$\tan(\alpha - \beta) = \dfrac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \tan(\beta)}\nonumber$$

If we specialize the sum formulas in Theorem 10.16 to the case when $\alpha = \beta$, we obtain the following ‘Double Angle’ Identities.

Theorem 10.17. Double Angle Identities

For all applicable angles $\theta$,

• $\cos(2\theta) = \left\{ \begin{array}{l} \cos^{2}(\theta) - \sin^{2}(\theta)\\[4pt] 2\cos^{2}(\theta) - 1 \\[4pt] 1-2\sin^{2}(\theta) \end{array} \right.$
• $\sin(2\theta) = 2\sin(\theta)\cos(\theta)$
• $\tan(2\theta) = \dfrac{2\tan(\theta)}{1 - \tan^{2}(\theta)}$

The three different forms for $\cos(2\theta)$ can be explained by our ability to ‘exchange’ squares of cosine and sine via the Pythagorean Identity $\cos^{2}(\theta) + \sin^{2}(\theta) = 1$ and we leave the details to the reader. It is interesting to note that to determine the value of $\cos(2\theta)$, only one piece of information is required: either $\cos(\theta)$ or $\sin(\theta)$. To determine $\sin(2\theta)$, however, it appears that we must know both $\sin(\theta)$ and $\cos(\theta)$. In the next example, we show how we can find $\sin(2\theta)$ knowing just one piece of information, namely $\tan(\theta)$.

Example 10.4.3

1. Suppose $P(-3,4)$ lies on the terminal side of $\theta$ when $\theta$ is plotted in standard position. Find $\cos(2\theta)$ and $\sin(2\theta)$ and determine the quadrant in which the terminal side of the angle $2\theta$ lies when it is plotted in standard position.
2. If $\sin(\theta) = x$ for $-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}$, find an expression for $\sin(2\theta)$ in terms of $x$.
3. [doubleanglesinewtan] Verify the identity: $\sin(2\theta) = \dfrac{2\tan(\theta)}{1 + \tan^{2}(\theta)}$.
4. Express $\cos(3\theta)$ as a polynomial in terms of $\cos(\theta)$.

Solution.

1. Using Theorem 10.3 from Section 10.2 with $x = -3$ and $y=4$, we find $r = \sqrt{x^2+y^2} = 5$. Hence, $\cos(\theta) = -\frac{3}{5}$ and $\sin(\theta) = \frac{4}{5}$. Applying Theorem 10.17, we get $\cos(2\theta) = \cos^{2}(\theta) - \sin^{2}(\theta) = \left(-\frac{3}{5}\right)^2 - \left(\frac{4}{5}\right)^2 = -\frac{7}{25}$, and $\sin(2\theta) = 2 \sin(\theta) \cos(\theta) = 2 \left(\frac{4}{5}\right)\left(-\frac{3}{5}\right) = -\frac{24}{25}$. Since both cosine and sine of $2\theta$ are negative, the terminal side of $2\theta$, when plotted in standard position, lies in Quadrant III.
2. If your first reaction to ‘$\sin(\theta) = x$’ is ‘No it’s not, $\cos(\theta) = x$!’ then you have indeed learned something, and we take comfort in that. However, context is everything. Here, ‘$x$’ is just a variable - it does not necessarily represent the $x$-coordinate of the point on The Unit Circle which lies on the terminal side of $\theta$, assuming $\theta$ is drawn in standard position. Here, $x$ represents the quantity $\sin(\theta)$, and what we wish to know is how to express $\sin(2\theta)$ in terms of $x$. We will see more of this kind of thing in Section 10.6, and, as usual, this is something we need for Calculus. Since $\sin(2\theta) = 2 \sin(\theta) \cos(\theta)$, we need to write $\cos(\theta)$ in terms of $x$ to finish the problem. We substitute $x = \sin(\theta)$ into the Pythagorean Identity, $\cos^{2}(\theta) + \sin^{2}(\theta) = 1$, to get $\cos^{2}(\theta) + x^2 = 1$, or $\cos(\theta) = \pm \sqrt{1-x^2}$. Since $-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}$, $\cos(\theta) \geq 0$, and thus $\cos(\theta) = \sqrt{1-x^2}$. Our final answer is $\sin(2\theta) = 2 \sin(\theta) \cos(\theta) = 2x\sqrt{1-x^2}$.
3. We start with the right hand side of the identity and note that $1 + \tan^{2}(\theta) = \sec^{2}(\theta)$. From this point, we use the Reciprocal and Quotient Identities to rewrite $\tan(\theta)$ and $\sec(\theta)$ in terms of $\cos(\theta)$ and $\sin(\theta)$:

   $$\begin{array}{rcl} \dfrac{2\tan(\theta)}{1 + \tan^{2}(\theta)} & = & \dfrac{2\tan(\theta)}{\sec^{2}(\theta)}= \dfrac{2 \left( \dfrac{\sin(\theta)}{\cos(\theta)}\right)}{\dfrac{1}{\cos^{2}(\theta)}}= 2\left( \dfrac{\sin(\theta)}{\cos(\theta)}\right) \cos^{2}(\theta) \\[15pt] & = & 2\left( \dfrac{\sin(\theta)}{\cancel{\cos(\theta)}}\right) \cancel{\cos(\theta)} \cos(\theta) = 2\sin(\theta) \cos(\theta) = \sin(2\theta) \\ \end{array}\nonumber$$

4. In Theorem 10.17, one of the formulas for $\cos(2\theta)$, namely $\cos(2\theta) = 2\cos^{2}(\theta) - 1$, expresses $\cos(2\theta)$ as a polynomial in terms of $\cos(\theta)$. We are now asked to find such an identity for $\cos(3\theta)$. Using the sum formula for cosine, we begin with

   $$\begin{array}{rcl} \cos(3\theta) & = & \cos(2\theta + \theta) \\[4pt] & = & \cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta) \\ \end{array}\nonumber$$

   Our ultimate goal is to express the right hand side in terms of $\cos(\theta)$ only. We substitute $\cos(2\theta) = 2\cos^{2}(\theta) -1$ and $\sin(2\theta) = 2\sin(\theta)\cos(\theta)$ which yields

   $$\begin{array}{rcl} \cos(3\theta) & = & \cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta) \\[4pt] & = & \left(2\cos^{2}(\theta) - 1\right) \cos(\theta) - \left(2 \sin(\theta) \cos(\theta) \right)\sin(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \sin^2(\theta) \cos(\theta) \\ \end{array}\nonumber$$

   Finally, we exchange $\sin^{2}(\theta)$ for $1 - \cos^{2}(\theta)$ courtesy of the Pythagorean Identity, and get

   $$\begin{array}{rcl} \cos(3\theta) & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \sin^2(\theta) \cos(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2 \left(1 - \cos^{2}(\theta)\right) \cos(\theta) \\[4pt] & = & 2\cos^{3}(\theta)- \cos(\theta) - 2\cos(\theta) + 2\cos^{3}(\theta) \\[4pt] & = & 4\cos^{3}(\theta)- 3\cos(\theta) \\ \end{array}\nonumber$$ and we are done.

In the last problem in Example 10.4.3, we saw how we could rewrite $\cos(3\theta)$ as sums of powers of $\cos(\theta)$. In Calculus, we have occasion to do the reverse; that is, reduce the power of cosine and sine. Solving the identity $\cos(2\theta) = 2\cos^{2}(\theta) -1$ for $\cos^{2}(\theta)$ and the identity $\cos(2\theta) = 1 - 2\sin^{2}(\theta)$ for $\sin^{2}(\theta)$ results in the aptly-named ‘Power Reduction’ formulas below.

Theorem 10.18. Power Reduction Formulas

For all angles $\theta$,

• $\cos^{2}(\theta) = \dfrac{1 + \cos(2\theta)}{2}$
• $\sin^{2}(\theta) = \dfrac{1 - \cos(2\theta)}{2}$

Example 10.4.4

Rewrite $\sin ^{2}(\theta) \cos ^{2}(\theta)$ as a sum and difference of cosines to the first power.

Solution

We begin with a straightforward application of Theorem 10.18

$$\begin{array}{rcl} \sin^{2}(\theta) \cos^{2}(\theta) & = & \left( \dfrac{1 - \cos(2\theta)}{2} \right) \left( \dfrac{1 + \cos(2\theta)}{2} \right) \\ [10pt] & = & \dfrac{1}{4}\left(1 - \cos^{2}(2\theta)\right) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{4}\cos^{2}(2\theta) \\ \end{array}\nonumber$$

Next, we apply the power reduction formula to $\cos^{2}(2\theta)$ to finish the reduction

$$\begin{array}{rcl} \sin^{2}(\theta) \cos^{2}(\theta) & = & \dfrac{1}{4} - \dfrac{1}{4}\cos^{2}(2\theta) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{4} \left(\dfrac{1 + \cos(2(2\theta))}{2}\right) \\ [10pt] & = & \dfrac{1}{4} - \dfrac{1}{8} - \dfrac{1}{8}\cos(4\theta) \\ [10pt] & = & \dfrac{1}{8} - \dfrac{1}{8}\cos(4\theta) \\ \end{array}\nonumber$$

Another application of the Power Reduction Formulas is the Half Angle Formulas. To start, we apply the Power Reduction Formula to $\cos^{2}\left(\frac{\theta}{2}\right)$

$$\cos^{2}\left(\dfrac{\theta}{2}\right) = \dfrac{1 + \cos\left(2 \left(\frac{\theta}{2}\right)\right)}{2} = \dfrac{1 + \cos(\theta)}{2}.\nonumber$$

We can obtain a formula for $\cos\left(\frac{\theta}{2}\right)$ by extracting square roots. In a similar fashion, we may obtain a half angle formula for sine, and by using a quotient formula, obtain a half angle formula for tangent. We summarize these formulas below.

Theorem 10.19. Half Angle Formulas

For all applicable angles $\theta$,

• $\cos\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 + \cos(\theta)}{2}}$
• $\sin\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 - \cos(\theta)}{2}}$
• $\tan\left(\dfrac{\theta}{2}\right) = \pm \sqrt{\dfrac{1 - \cos(\theta)}{1+\cos(\theta)}}$

where the choice of $\pm$ depends on the quadrant in which the terminal side of $\dfrac{\theta}{2}$ lies.

Example 10.4.5

1. Use a half angle formula to find the exact value of $\cos\left(15^{\circ}\right)$.
2. Suppose $-\pi \leq \theta \leq 0$ with $\cos(\theta) = -\frac{3}{5}$. Find $\sin\left(\frac{\theta}{2}\right)$.
3. Use the identity given in number 3 of Example 10.4.3 to derive the identity $$\tan\left(\dfrac{\theta}{2}\right) = \dfrac{\sin(\theta)}{1+\cos(\theta)}\nonumber$$

Solution

1. To use the half angle formula, we note that $15^{\circ} = \frac{30^{\circ}}{2}$ and since $15^{\circ}$ is a Quadrant I angle, its cosine is positive. Thus we have

   $$\begin{array}{rcl} \cos\left(15^{\circ}\right) & = & + \sqrt{\dfrac{1+\cos\left(30^{\circ}\right)}{2}} = \sqrt{\dfrac{1+\frac{\sqrt{3}}{2}}{2}}\\ [10pt] & = & \sqrt{\dfrac{1+\frac{\sqrt{3}}{2}}{2}\cdot \dfrac{2}{2}} = \sqrt{\dfrac{2+\sqrt{3}}{4}} = \dfrac{\sqrt{2+\sqrt{3}}}{2}\\ \end{array}\nonumber$$

   Back in Example 10.4.1, we found $\cos\left(15^{\circ}\right)$ by using the difference formula for cosine. In that case, we determined $\cos\left(15^{\circ}\right) = \frac{\sqrt{6}+ \sqrt{2}}{4}$. The reader is encouraged to prove that these two expressions are equal.

2. If $-\pi \leq \theta \leq 0$, then $-\frac{\pi}{2} \leq \frac{\theta}{2} \leq 0$, which means $\sin\left(\frac{\theta}{2}\right) < 0$. Theorem 10.19 gives

   $$\begin{array}{rcl} \sin\left(\dfrac{\theta}{2} \right) & = & -\sqrt{\dfrac{1-\cos\left(\theta \right)}{2}} = -\sqrt{\dfrac{1- \left(-\frac{3}{5}\right)}{2}}\\ [10pt] & = & -\sqrt{\dfrac{1 + \frac{3}{5}}{2} \cdot \dfrac{5}{5}} = -\sqrt{\dfrac{8}{10}} = -\dfrac{2\sqrt{5}}{5}\\ \end{array}\nonumber$$

3. Instead of our usual approach to verifying identities, namely starting with one side of the equation and trying to transform it into the other, we will start with the identity we proved in number 3 of Example 10.4.3 and manipulate it into the identity we are asked to prove. The identity we are asked to start with is $\; \sin(2\theta) = \frac{2\tan(\theta)}{1 + \tan^{2}(\theta)}$. If we are to use this to derive an identity for $\tan\left(\frac{\theta}{2}\right)$, it seems reasonable to proceed by replacing each occurrence of $\theta$ with $\frac{\theta}{2}$

   $$\begin{array}{rcl} \sin\left(2 \left(\frac{\theta}{2}\right)\right) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\ \end{array}\nonumber$$

   We now have the $\sin(\theta)$ we need, but we somehow need to get a factor of $1+\cos(\theta)$ involved. To get cosines involved, recall that $1 + \tan^{2}\left(\frac{\theta}{2}\right) = \sec^{2}\left(\frac{\theta}{2}\right)$. We continue to manipulate our given identity by converting secants to cosines and using a power reduction formula

   $$\begin{array}{rcl} \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{1 + \tan^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & \dfrac{2\tan\left(\frac{\theta}{2}\right)}{\sec^{2}\left(\frac{\theta}{2}\right)} \\[15pt] \sin(\theta) & = & 2 \tan\left(\frac{\theta}{2}\right) \cos^{2}\left(\frac{\theta}{2}\right) \\[4pt] \sin(\theta) & = & 2 \tan\left(\frac{\theta}{2}\right) \left(\dfrac{1 + \cos\left(2 \left(\frac{\theta}{2}\right)\right)}{2}\right) \\[15pt] \sin(\theta) & = & \tan\left(\frac{\theta}{2}\right) \left(1+\cos(\theta) \right) \\[4pt] \tan\left(\dfrac{\theta}{2}\right) & = & \dfrac{\sin(\theta)}{1+\cos(\theta)} \\ \end{array}\nonumber$$

Our next batch of identities, the Product to Sum Formulas,³ are easily verified by expanding each of the right hand sides in accordance with Theorem 10.16 and as you should expect by now we leave the details as exercises. They are of particular use in Calculus, and we list them here for reference.

Theorem 10.20. Product to Sum Formulas

For all angles $\alpha$ and $\beta$,

• $\cos(\alpha)\cos(\beta) = \frac{1}{2} \left[ \cos(\alpha - \beta) + \cos(\alpha + \beta)\right]$
• $\sin(\alpha)\sin(\beta) = \frac{1}{2} \left[ \cos(\alpha - \beta) - \cos(\alpha + \beta)\right]$
• $\sin(\alpha)\cos(\beta) = \frac{1}{2} \left[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\right]$

Related to the Product to Sum Formulas are the Sum to Product Formulas, which we will have need of in Section 10.7. These are easily verified using the Product to Sum Formulas, and as such, their proofs are left as exercises.

Theorem 10.21. Sum to Product Formulastoproduct

For all angles $\alpha$ and $\beta$,

• $\cos(\alpha) + \cos(\beta) = 2 \cos\left( \dfrac{\alpha + \beta}{2}\right)\cos\left( \dfrac{\alpha - \beta}{2}\right)$
• $\cos(\alpha) - \cos(\beta) = - 2 \sin\left( \dfrac{\alpha + \beta}{2}\right)\sin\left( \dfrac{\alpha - \beta}{2}\right)$
• $\sin(\alpha) \pm \sin(\beta) = 2 \sin\left( \dfrac{\alpha \pm \beta}{2}\right)\cos\left( \dfrac{\alpha \mp \beta}{2}\right)$

Example 10.4.6

1. Write $\; \cos(2\theta)\cos(6\theta) \;$ as a sum.
2. Write $\; \sin(\theta) - \sin(3\theta) \;$ as a product.

Solution.

1. Identifying $\alpha = 2\theta$ and $\beta = 6\theta$, we find

   $$\begin{array}{rcl} \cos(2\theta)\cos(6\theta) & = & \frac{1}{2} \left[ \cos(2\theta - 6\theta) + \cos(2\theta + 6\theta)\right]\\ [4pt] & = & \frac{1}{2} \cos(-4\theta) + \frac{1}{2}\cos(8\theta) \\ [4pt] & = & \frac{1}{2} \cos(4\theta) + \frac{1}{2} \cos(8\theta), \end{array}\nonumber$$ where the last equality is courtesy of the even identity for cosine, $\cos(-4\theta) = \cos(4\theta)$.

2. Identifying $\alpha = \theta$ and $\beta = 3\theta$ yields

   $$\begin{array}{rcl} \sin(\theta) - \sin(3\theta) & = & 2 \sin\left( \dfrac{\theta - 3\theta}{2}\right)\cos\left( \dfrac{\theta + 3\theta}{2}\right) \\[4pt] & = & 2 \sin\left( -\theta \right)\cos\left( 2\theta \right) \\[4pt] & = & -2 \sin\left( \theta \right)\cos\left( 2\theta \right), \\ \end{array}\nonumber$$ where the last equality is courtesy of the odd identity for sine, $\sin(-\theta) = -\sin(\theta)$.

The reader is reminded that all of the identities presented in this section which regard the circular functions as functions of angles (in radian measure) apply equally well to the circular (trigonometric) functions regarded as functions of real numbers. In Exercises 38 - 43 in Section 10.5, we see how some of these identities manifest themselves geometrically as we study the graphs of the these functions. In the upcoming Exercises, however, you need to do all of your work analytically without graphs.

10.4.1. Exercises

In Exercises 1 - 6, use the Even / Odd Identities to verify the identity. Assume all quantities are defined.

1. $\sin(3\pi - 2\theta) = -\sin(2\theta - 3\pi)$
2. $\cos \left( -\dfrac{\pi}{4} - 5t \right) = \cos \left( 5t + \dfrac{\pi}{4} \right)$
3. $\tan(-t^{2} + 1) = -\tan(t^{2} - 1)$
4. $\csc(-\theta - 5) = -\csc(\theta + 5)$
5. $\sec(-6t) = \sec(6t)$
6. $\cot(9 - 7\theta) = -\cot(7\theta - 9)$

In Exercises 7 - 21, use the Sum and Difference Identities to find the exact value. You may have need of the Quotient, Reciprocal or Even / Odd Identities as well.

7. $\cos(75^{\circ})$
8. $\sec(165^{\circ})$
9. $\sin(105^{\circ})$
10. $\csc(195^{\circ})$
11. $\cot(255^{\circ})$
12. $\tan(375^{\circ})$
13. $\cos\left(\dfrac{13\pi}{12}\right)$
14. $\sin\left(\dfrac{11\pi}{12}\right)$
15. $\tan\left(\dfrac{13\pi}{12}\right)$
16. [cos7pi12] $\cos \left( \dfrac{7\pi}{12} \right)$
17. $\tan \left( \dfrac{17\pi}{12} \right)$
18. $\sin \left( \dfrac{\pi}{12} \right)$
19. $\cot \left( \dfrac{11\pi}{12} \right)$
20. $\csc \left( \dfrac{5\pi}{12} \right)$
21. $\sec \left( -\dfrac{\pi}{12} \right)$
22. If $\alpha$ is a Quadrant IV angle with $\cos(\alpha) = \dfrac{\sqrt{5}}{5}$, and $\sin(\beta) = \dfrac{\sqrt{10}}{10}$, where $\dfrac{\pi}{2} < \beta < \pi$, find
    1. $\cos(\alpha + \beta)$
    2. $\sin(\alpha + \beta)$
    3. $\tan(\alpha + \beta)$
    4. $\cos(\alpha - \beta)$
    5. $\sin(\alpha - \beta)$
    6. $\tan(\alpha - \beta)$
23. If $\csc(\alpha) = 3$, where $0 < \alpha < \dfrac{\pi}{2}$, and $\beta$ is a Quadrant II angle with $\tan(\beta) = -7$, find
    1. $\cos(\alpha + \beta)$
    2. $\sin(\alpha + \beta)$
    3. $\tan(\alpha + \beta)$
    4. $\cos(\alpha - \beta)$
    5. $\sin(\alpha - \beta)$
    6. $\tan(\alpha - \beta)$
24. If $\sin(\alpha) = \dfrac{3}{5}$, where $0 < \alpha < \dfrac{\pi}{2}$, and $\cos(\beta) = \dfrac{12}{13}$ where $\dfrac{3\pi}{2} < \beta < 2\pi$, find
    1. $\sin(\alpha + \beta)$
    2. $\cos(\alpha - \beta)$
    3. $\tan(\alpha - \beta)$
25. If $\sec(\alpha) = -\dfrac{5}{3}$, where $\dfrac{\pi}{2} < \alpha < \pi$, and $\tan(\beta) = \dfrac{24}{7}$, where $\pi < \beta < \dfrac{3\pi}{2}$, find
    1. $\csc(\alpha - \beta)$
    2. $\sec(\alpha + \beta)$
    3. $\cot(\alpha + \beta)$

In Exercises 26 - 38, verify the identity.

26. $\cos(\theta - \pi) = -\cos(\theta)$
27. $\sin(\pi - \theta) = \sin(\theta)$
28. $\tan\left(\theta + \dfrac{\pi}{2} \right) = -\cot(\theta)$
29. $\sin(\alpha + \beta) + \sin(\alpha - \beta) = 2\sin(\alpha)\cos(\beta)$
30. $\sin(\alpha + \beta) - \sin(\alpha - \beta) = 2\cos(\alpha) \sin(\beta)$
31. $\cos(\alpha + \beta) + \cos(\alpha - \beta) = 2\cos(\alpha) \cos(\beta)$
32. $\cos(\alpha + \beta) - \cos(\alpha - \beta) = -2\sin(\alpha) \sin(\beta)$
33. $\dfrac{\sin(\alpha+\beta)}{\sin(\alpha-\beta)} = \dfrac{1+\cot(\alpha) \tan(\beta)}{1 - \cot(\alpha) \tan(\beta)}$
34. $\dfrac{\cos(\alpha + \beta)}{\cos(\alpha - \beta)} = \dfrac{1 - \tan(\alpha)\tan(\beta)}{1 + \tan(\alpha)\tan(\beta)}$
35. $\dfrac{\tan(\alpha + \beta)}{\tan(\alpha - \beta)} = \dfrac{\sin(\alpha)\cos(\alpha) + \sin(\beta)\cos(\beta)}{\sin(\alpha)\cos(\alpha) - \sin(\beta)\cos(\beta)}$
36. $\dfrac{\sin(t + h) - \sin(t)}{h} = \cos(t) \left(\dfrac{\sin(h)}{h} \right) + \sin(t) \left( \dfrac{\cos(h) - 1}{h} \right)$
37. $\dfrac{\cos(t + h) - \cos(t)}{h} = \cos(t) \left( \dfrac{\cos(h) - 1}{h} \right) - \sin(t) \left(\dfrac{\sin(h)}{h} \right)$
38. $\dfrac{\tan(t + h) - \tan(t)}{h} = \left( \dfrac{\tan(h)}{h} \right) \left(\dfrac{\sec^{2}(t)}{1 - \tan(t)\tan(h)} \right)$

In Exercises 39 - 48, use the Half Angle Formulas to find the exact value. You may have need of the Quotient, Reciprocal or Even / Odd Identities as well.

39. $\cos(75^{\circ})$ (compare with Exercise 7)
40. $\sin(105^{\circ})$ (compare with Exercise 9)
41. $\cos(67.5^{\circ})$
42. $\sin(157.5^{\circ})$
43. $\tan(112.5^{\circ})$
44. $\cos\left( \dfrac{7\pi}{12} \right)$ (compare with Exercise 16)
45. $\sin\left( \dfrac{\pi}{12} \right)$ (compare with Exercise 18)
46. $\cos \left( \dfrac{\pi}{8} \right)$
47. $\sin \left( \dfrac{5\pi}{8} \right)$
48. $\tan \left( \dfrac{7\pi}{8} \right)$

In Exercises 49 - 58, use the given information about $\theta$ to find the exact values of

• $\sin(2\theta)$
• $\sin\left(\dfrac{\theta}{2}\right)$
• $\cos(2\theta)$
• $\cos\left(\dfrac{\theta}{2}\right)$
• $\tan(2\theta)$
• $\tan\left(\dfrac{\theta}{2}\right)$

49. $\sin(\theta) = -\dfrac{7}{25}$ where $\dfrac{3\pi}{2} < \theta < 2\pi$
50. $\cos(\theta) = \dfrac{28}{53}$ where $0 < \theta < \dfrac{\pi}{2}$
51. $\tan(\theta) = \dfrac{12}{5}$ where $\pi < \theta < \dfrac{3\pi}{2}$
52. $\csc(\theta) = 4$ where $\dfrac{\pi}{2} < \theta < \pi$
53. $\cos(\theta) = \dfrac{3}{5}$ where $0 < \theta < \dfrac{\pi}{2}$
54. $\sin(\theta) = -\dfrac{4}{5}$ where $\pi < \theta < \dfrac{3\pi}{2}$
55. $\cos(\theta) = \dfrac{12}{13}$ where $\dfrac{3\pi}{2} < \theta < 2\pi$
56. $\sin(\theta) = \dfrac{5}{13}$ where $\dfrac{\pi}{2} < \theta < \pi$
57. $\sec(\theta) = \sqrt{5}$ where $\dfrac{3\pi}{2} < \theta < 2\pi$
58. $\tan(\theta) = -2$ where $\dfrac{\pi}{2} < \theta < \pi$

In Exercises 59 - 73, verify the identity. Assume all quantities are defined.

59. $(\cos(\theta) + \sin(\theta))^2 = 1 + \sin(2\theta)$
60. $(\cos(\theta) - \sin(\theta))^2 = 1 - \sin(2\theta)$
61. $\tan(2\theta) = \dfrac{1}{1-\tan(\theta)} - \dfrac{1}{1+\tan(\theta)}$
62. $\csc(2\theta) = \dfrac{\cot(\theta) + \tan(\theta)}{2}$
63. $8 \sin^{4}(\theta) = \cos(4\theta) - 4\cos(2\theta)+3$
64. $8 \cos^{4}(\theta) = \cos(4\theta) + 4\cos(2\theta)+3$
65. [sine3theta] $\sin(3\theta) = 3\sin(\theta) - 4\sin^{3}(\theta)$
66. $\sin(4\theta) = 4\sin(\theta)\cos^{3}(\theta) - 4\sin^{3}(\theta)\cos(\theta)$
67. $32\sin^{2}(\theta) \cos^{4}(\theta) = 2 + \cos(2\theta) - 2\cos(4\theta) - \cos(6\theta)$
68. $32\sin^{4}(\theta) \cos^{2}(\theta) = 2 - \cos(2\theta) - 2\cos(4\theta) + \cos(6\theta)$
69. $\cos(4\theta) = 8\cos^{4}(\theta) - 8\cos^{2}(\theta) + 1$
70. $\cos(8\theta) = 128\cos^{8}(\theta)-256\cos^{6}(\theta)+160\cos^{4}(\theta)-32\cos^{2}(\theta)+1$ (HINT: Use the result to 69.)
71. $\sec(2\theta) = \dfrac{\cos(\theta)}{\cos(\theta) + \sin(\theta)} + \dfrac{\sin(\theta)}{\cos(\theta)-\sin(\theta)}$
72. $\dfrac{1}{\cos(\theta) - \sin(\theta)} + \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\cos(\theta)}{\cos(2\theta)}$
73. $\dfrac{1}{\cos(\theta) - \sin(\theta)} - \dfrac{1}{\cos(\theta) + \sin(\theta)} = \dfrac{2\sin(\theta)}{\cos(2\theta)}$

In Exercises 74 - 79, write the given product as a sum. You may need to use an Even/Odd Identity.

74. $\cos(3\theta)\cos(5\theta)$
75. $\sin(2\theta)\sin(7\theta)$
76. $\sin(9\theta)\cos(\theta)$
77. $\cos(2\theta) \cos(6\theta)$
78. $\sin(3\theta) \sin(2\theta)$
79. $\cos(\theta) \sin(3\theta)$

In Exercises 80 - 85, write the given sum as a product. You may need to use an Even/Odd or Cofunction Identity.

80. $\cos(3\theta) + \cos(5\theta)$
81. $\sin(2\theta) - \sin(7\theta)$
82. $\cos(5\theta) - \cos(6\theta)$
83. $\sin(9\theta) - \sin(-\theta)$
84. $\sin(\theta) + \cos(\theta)$
85. $\cos(\theta) - \sin(\theta)$
86. Suppose $\theta$ is a Quadrant I angle with $\sin(\theta) = x$. Verify the following formulas
    1. $\cos(\theta) = \sqrt{1-x^2}$
    2. $\sin(2\theta) = 2x\sqrt{1-x^2}$
    3. $\cos(2\theta) = 1 - 2x^2$
87. Discuss with your classmates how each of the formulas, if any, in Exercise 86 change if we change assume $\theta$ is a Quadrant II, III, or IV angle.
88. Suppose $\theta$ is a Quadrant I angle with $\tan(\theta) = x$. Verify the following formulas
    1. $\cos(\theta) = \dfrac{1}{\sqrt{x^2+1}}$
    2. $\sin(\theta) = \dfrac{x}{\sqrt{x^2+1}}$
    3. $\sin(2\theta) = \dfrac{2x}{x^2+1}$
    4. $\cos(2\theta) = \dfrac{1-x^2}{x^2+1}$
89. Discuss with your classmates how each of the formulas, if any, in Exercise 88 change if we change assume $\theta$ is a Quadrant II, III, or IV angle.
90. If $\sin(\theta) = \dfrac{x}{2}$ for $-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}$, find an expression for $\cos(2\theta)$ in terms of $x$.
91. If $\tan(\theta) = \dfrac{x}{7}$ for $-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}$, find an expression for $\sin(2\theta)$ in terms of $x$.
92. If $\sec(\theta) = \dfrac{x}{4}$ for $0 < \theta < \dfrac{\pi}{2}$, find an expression for $\ln|\sec(\theta) + \tan(\theta)|$ in terms of $x$.
93. Show that $\cos^{2}(\theta) - \sin^{2}(\theta) = 2\cos^{2}(\theta) - 1 = 1 - 2\sin^{2}(\theta)$ for all $\theta$.
94. Let $\theta$ be a Quadrant III angle with $\cos(\theta) = -\dfrac{1}{5}$. Show that this is not enough information to determine the sign of $\sin\left(\dfrac{\theta}{2}\right)$ by first assuming $3\pi < \theta < \dfrac{7\pi}{2}$ and then assuming $\pi < \theta < \dfrac{3\pi}{2}$ and computing $\sin\left(\dfrac{\theta}{2}\right)$ in both cases.
95. Without using your calculator, show that $\dfrac{\sqrt{2 + \sqrt{3}}}{2} = \dfrac{\sqrt{6} + \sqrt{2}}{4}$
96. In part 4 of Example 10.4.3, we wrote $\cos(3\theta)$ as a polynomial in terms of $\cos(\theta)$. In Exercise 69, we had you verify an identity which expresses $\cos(4\theta)$ as a polynomial in terms of $\cos(\theta)$. Can you find a polynomial in terms of $\cos(\theta)$ for $\cos(5\theta)$? $\cos(6\theta)$? Can you find a pattern so that $\cos(n\theta)$ could be written as a polynomial in cosine for any natural number $n$?
97. In Exercise 65, we has you verify an identity which expresses $\sin(3\theta)$ as a polynomial in terms of $\sin(\theta)$. Can you do the same for $\sin(5\theta)$? What about for $\sin(4\theta)$? If not, what goes wrong?
98. Verify the Even / Odd Identities for tangent, secant, cosecant and cotangent.
99. Verify the Cofunction Identities for tangent, secant, cosecant and cotangent.
100. Verify the Difference Identities for sine and tangent.
101. Verify the Product to Sum Identities.
102. Verify the Sum to Product Identities.

10.4.2. Answers

7. $\cos(75^{\circ}) = \dfrac{\sqrt{6} - \sqrt{2}}{4}$
8. $\sec(165^{\circ}) = -\dfrac{4}{\sqrt{2}+\sqrt{6}} = \sqrt{2} - \sqrt{6}$
9. $\sin(105^{\circ}) = \dfrac{\sqrt{6}+\sqrt{2}}{4}$
10. $\csc(195^{\circ}) = \dfrac{4}{\sqrt{2}-\sqrt{6}} = -(\sqrt{2}+\sqrt{6})$
11. $\cot(255^{\circ}) = \dfrac{\sqrt{3}-1}{\sqrt{3}+1} = 2-\sqrt{3}$
12. $\tan(375^{\circ}) = \dfrac{3-\sqrt{3}}{3+\sqrt{3}} = 2-\sqrt{3}$
13. $\cos\left(\dfrac{13\pi}{12}\right) = -\dfrac{\sqrt{6}+\sqrt{2}}{4}$
14. $\sin\left(\dfrac{11\pi}{12}\right) = \dfrac{\sqrt{6} - \sqrt{2}}{4}$
15. $\tan\left(\dfrac{13\pi}{12}\right) = \dfrac{3-\sqrt{3}}{3+\sqrt{3}} = 2-\sqrt{3}$
16. $\cos \left( \dfrac{7\pi}{12} \right) = \dfrac{\sqrt{2} - \sqrt{6}}{4}$
17. $\tan \left( \dfrac{17\pi}{12} \right) = 2 + \sqrt{3}$
18. $\sin \left( \dfrac{\pi}{12} \right) = \dfrac{\sqrt{6} - \sqrt{2}}{4}$
19. $\cot \left( \dfrac{11\pi}{12} \right) = -(2 + \sqrt{3})$
20. $\csc \left( \dfrac{5\pi}{12} \right) = \sqrt{6} - \sqrt{2}$
21. $\sec \left( -\dfrac{\pi}{12} \right) = \sqrt{6} - \sqrt{2}$
22. 1. $\cos(\alpha + \beta) = -\dfrac{\sqrt{2}}{10}$
    2. $\sin(\alpha + \beta) = \dfrac{7\sqrt{2}}{10}$
    3. $\sin(\alpha - \beta) = \dfrac{\sqrt{2}}{2}$
    4. $\tan(\alpha - \beta) = -1$
    5. $\tan(\alpha + \beta) = -7$
    6. $\cos(\alpha - \beta)= -\dfrac{\sqrt{2}}{2}$
23. 1. $\cos(\alpha + \beta) = - \dfrac{4+7\sqrt{2}}{30}$
    2. $\sin(\alpha + \beta) = \dfrac{28-\sqrt{2}}{30}$
    3. $\sin(\alpha - \beta) = - \dfrac{28+\sqrt{2}}{30}$
    4. $\tan(\alpha - \beta)= \dfrac{28+\sqrt{2}}{4-7\sqrt{2}} = -\dfrac{63+100\sqrt{2}}{41}$
    5. $\tan(\alpha + \beta) = \dfrac{-28+\sqrt{2}}{4+7\sqrt{2}} = \dfrac{63-100\sqrt{2}}{41}$
    6. $\cos(\alpha - \beta) = \dfrac{-4+7\sqrt{2}}{30}$
24. 1. $\sin(\alpha + \beta) = \dfrac{16}{65}$
    2. $\cos(\alpha - \beta) = \dfrac{33}{65}$
    3. $\tan(\alpha - \beta) = \dfrac{56}{33}$
25. 1. $\csc(\alpha - \beta) = -\dfrac{5}{4}$
    2. $\sec(\alpha + \beta) = \dfrac{125}{117}$
    3. $\cot(\alpha + \beta) = \dfrac{117}{44}$

39. $\cos(75^{\circ}) = \dfrac{\sqrt{2-\sqrt{3}}}{2}$
40. $\sin(105^{\circ}) = \dfrac{\sqrt{2+\sqrt{3}}}{2}$
41. $\cos(67.5^{\circ}) = \dfrac{\sqrt{2-\sqrt{2}}}{2}$
42. $\sin(157.5^{\circ}) = \dfrac{\sqrt{2-\sqrt{2}}}{2}$
43. $\tan(112.5^{\circ}) = - \sqrt{\dfrac{2+\sqrt{2}}{2-\sqrt{2}}} = -1 - \sqrt{2}$
44. $\cos\left( \dfrac{7\pi}{12} \right) = -\dfrac{\sqrt{2-\sqrt{3}}}{2}$
45. $\sin\left( \dfrac{\pi}{12} \right) = \dfrac{\sqrt{2-\sqrt{3}}}{2}$
46. $\cos \left( \dfrac{\pi}{8} \right) = \dfrac{\sqrt{2 + \sqrt{2}}}{2}$
47. $\sin \left( \dfrac{5\pi}{8} \right) = \dfrac{\sqrt{2 + \sqrt{2}}}{2}$
48. $\tan \left( \dfrac{7\pi}{8} \right) = -\sqrt{ \dfrac{2 - \sqrt{2}}{2 + \sqrt{2}} } =1-\sqrt{2}$
49. • $\sin(2\theta) = -\dfrac{336}{625}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{2}}{10}$
    • $\cos(2\theta) = \dfrac{527}{625}$
    • $\cos\left(\frac{\theta}{2}\right) = -\dfrac{7\sqrt{2}}{10}$
    • $\tan(2\theta) = -\dfrac{336}{527}$
    • $\tan\left(\frac{\theta}{2}\right) = -\dfrac{1}{7}$
50. • $\sin(2\theta) = \dfrac{2520}{2809}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{5\sqrt{106}}{106}$
    • $\cos(2\theta) = -\dfrac{1241}{2809}$
    • $\cos\left(\frac{\theta}{2}\right) = \dfrac{9\sqrt{106}}{106}$
    • $\tan(2\theta) = -\dfrac{2520}{1241}$
    • $\tan\left(\frac{\theta}{2}\right) = \dfrac{5}{9}$
51. • $\sin(2\theta) = \dfrac{120}{169}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{3\sqrt{13}}{13}$
    • $\cos(2\theta) = -\dfrac{119}{169}$
    • $\cos\left(\frac{\theta}{2}\right) = -\dfrac{2\sqrt{13}}{13}$
    • $\tan(2\theta) = -\dfrac{120}{119}$
    • $\tan\left(\frac{\theta}{2}\right) = -\dfrac{3}{2}$
52. • $\sin(2\theta) = -\dfrac{\sqrt{15}}{8}$
    • $\sin\left(\frac{\theta}{2}\right) =\dfrac{\sqrt{8+2\sqrt{15}}}{4} \\ \phantom{\tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}}$
    • $\cos(2\theta) = \dfrac{7}{8}$
    • $\cos\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{8-2\sqrt{15}}}{4} \\ \phantom{\tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}}$
    • $\tan(2\theta) = -\dfrac{\sqrt{15}}{7}$
    • $\tan\left(\frac{\theta}{2}\right) = \sqrt{\dfrac{8+2\sqrt{15}}{8-2\sqrt{15}}} \\ \tan\left(\frac{\theta}{2}\right) = 4+\sqrt{15}$
53. • $\sin(2\theta) = \dfrac{24}{25}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{5}}{5}$
    • $\cos(2\theta) = -\dfrac{7}{25}$
    • $\cos\left(\frac{\theta}{2}\right) = \dfrac{2\sqrt{5}}{5}$
    • $\tan(2\theta)=-\dfrac{24}{7}$
    • $\tan\left(\frac{\theta}{2}\right) = \dfrac{1}{2}$
54. • $\sin(2\theta) = \dfrac{24}{25}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{2\sqrt{5}}{5}$
    • $\cos(2\theta) = -\dfrac{7}{25}$
    • $\cos\left(\frac{\theta}{2}\right) = -\dfrac{\sqrt{5}}{5}$
    • $\tan(2\theta)=-\dfrac{24}{7}$
    • $\tan\left(\frac{\theta}{2}\right) = -2$
55. • $\sin(2\theta) = -\dfrac{120}{169}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{26}}{26}$
    • $\cos(2\theta) = \dfrac{119}{169}$
    • $\cos\left(\frac{\theta}{2}\right) = -\dfrac{5\sqrt{26}}{26}$
    • $\tan(2\theta)=-\dfrac{120}{119}$
    • $\tan\left(\frac{\theta}{2}\right) = -\dfrac{1}{5}$
56. • $\sin(2\theta) = -\dfrac{120}{169}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{5\sqrt{26}}{26}$
    • $\cos(2\theta) = \dfrac{119}{169}$
    • $\cos\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{26}}{26}$
    • $\tan(2\theta)=-\dfrac{120}{119}$
    • $\tan\left(\frac{\theta}{2}\right) = 5$
57. • $\sin(2\theta) = -\dfrac{4}{5}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{50-10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}$
    • $\cos(2\theta) = -\dfrac{3}{5}$
    • $\cos\left(\frac{\theta}{2}\right)= -\dfrac{\sqrt{50+10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}$
    • $\tan(2\theta)=\dfrac{4}{3}$
    • $\tan\left(\frac{\theta}{2}\right) = -\sqrt{\dfrac{5-\sqrt{5}}{5+\sqrt{5}}} \\ \tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}$
58. • $\sin(2\theta) = -\dfrac{4}{5}$
    • $\sin\left(\frac{\theta}{2}\right) = \dfrac{\sqrt{50+10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}$
    • $\cos(2\theta) = -\dfrac{3}{5}$
    • $\cos\left(\frac{\theta}{2}\right)= \dfrac{\sqrt{50-10\sqrt{5}}}{10} \\ \phantom{\tan\left(\frac{\theta}{2}\right) =\dfrac{5-5\sqrt{5}}{10}}$
    • $\tan(2\theta)=\dfrac{4}{3}$
    • $\tan\left(\frac{\theta}{2}\right) = \sqrt{\dfrac{5+\sqrt{5}}{5-\sqrt{5}}} \\ \tan\left(\frac{\theta}{2}\right) =\dfrac{5+5\sqrt{5}}{10}$

74. $\dfrac{\cos(2\theta) + \cos(8\theta)}{2}$
75. $\dfrac{\cos(5\theta) - \cos(9\theta)}{2}$
76. $\dfrac{\sin(8\theta) + \sin(10\theta)}{2}$
77. $\dfrac{\cos(4\theta) + \cos(8\theta)}{2}$
78. $\dfrac{\cos(\theta) - \cos(5\theta)}{2}$
79. $\dfrac{\sin(2\theta) + \sin(4\theta)}{2}$
80. $2\cos(4\theta)\cos(\theta)$
81. $-2\cos \left( \dfrac{9}{2}\theta \right) \sin \left( \dfrac{5}{2}\theta \right)$
82. $2\sin \left( \dfrac{11}{2}\theta \right) \sin \left( \dfrac{1}{2}\theta \right)$
83. $2\cos(4\theta)\sin(5\theta)$
84. $\sqrt{2}\cos \left(\theta - \dfrac{\pi}{4} \right)$
85. $-\sqrt{2}\sin \left(\theta - \dfrac{\pi}{4} \right)$

90. $1 - \dfrac{x^{2}}{2}$
91. $\dfrac{14x}{x^{2} + 49}$
92. $\ln |x + \sqrt{x^{2} + 16}| - \ln(4)$

---

Reference

¹ As mentioned at the end of Section 10.2, properties of the circular functions when thought of as functions of angles in radian measure hold equally well if we view these functions as functions of real numbers. Not surprisingly, the Even / Odd properties of the circular functions are so named because they identify cosine and secant as even functions, while the remaining four circular functions are odd. (See Section 1.6.)

² In the picture we’ve drawn, the triangles $POQ$ and $AOB$ are congruent, which is even better. However, $\alpha_{0}-\beta_{0}$ could be 0 or it could be $\pi$, neither of which makes a triangle. It could also be larger than $\pi$, which makes a triangle, just not the one we’ve drawn. You should think about those three cases.

³ These are also known as the Prosthaphaeresis Formulas and have a rich history. The authors recommend that you conduct some research on them as your schedule allows.