7.2: Inverse function
- Page ID
- 48990
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
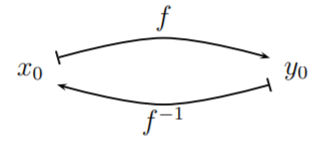
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A function is one-to-one, when each output is determined by exactly one input. Therefore we can construct a new function, called the inverse function, where we reverse the roles of inputs and outputs. For example, when \(y=x^3\), each \(y_0\) comes from exactly one \(x_0\) as shown in the picture below:
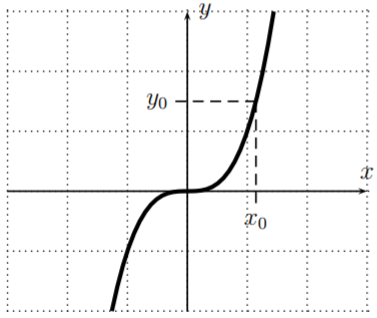
The inverse function assigns to the input \(y_0\) the output \(x_0\).
Let \(f\) be a function with domain \(D_f\) and range \(R_f\), and assume that \(f\) is one-to-one. The inverse of \(f\) is a function \(f^{-1}\) so that \[f(x)=y \quad \text{ means precisely that } \quad f^{-1}(y)=x \nonumber \]
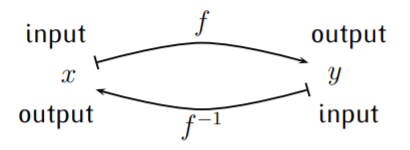
Here the outputs of \(f\) are the inputs of \(f^{-1}\), and the inputs of \(f\) are the outputs of \(f^{-1}\). Therefore, the inverse function \(f^{-1}\) has a domain equal to the range of \(f\), \(D_{f^{-1}}=R_f\), and \(f^{-1}\) has a range equal to the domain of \(f\), \(R_{f^{-1}}=D_f\). In short, when \(f\) is a function \(f:D_f\to R_f\), then the inverse function \(f^{-1}\) is a function \(f^{-1}:R_f\to D_f\).
The inverse function reverses the roles of inputs and outputs.
Find the inverse of the following function via algebra.
- \(f(x)=2x-7\)
- \(g(x)=\sqrt{x+2}\)
- \(h(x)=\dfrac{1}{x+4}\)
- \(j(x)=\dfrac{x+1}{x+2}\)
- \(k(x)=(x-2)^2+3\) for \(x\geq 2\)
Solution
- First, reverse the role of input and output in \(y=2x-7\) by exchanging the variables \(x\) and \(y\). That is, we write \(x=2y-7\). We need to solve this for \(y\): \[\stackrel{\text{(add $7$)}}\implies\quad x+7 = 2y \implies\quad y=\dfrac{x+7}{2} \nonumber \] Therefore, we obtain that the inverse of \(f\) is \(f^{-1}(x)=\dfrac{x+7} 2\).
For the other parts, we always exchange \(x\) and \(y\) and solve for \(y\):
- Write \(y=\sqrt{x+2}\) and exchange \(x\) and \(y\): \[\begin{aligned} x=\sqrt{y+2} &\implies & x^2 =y+2 \quad \implies y= x^2-2\\ &\implies & g^{-1}(x)=x^2-2\end{aligned} \nonumber \]
- Write \(y=\dfrac{1}{x+4}\) and exchange \(x\) and \(y\): \[\begin{aligned} x=\dfrac{1}{y+4}& \implies & y+4 =\dfrac 1 x \quad\implies y= \dfrac 1 x -4\\ &\implies& h^{-1}(x)=\dfrac 1 x -4\end{aligned} \nonumber \]
- Write \(y=\dfrac{x+1}{x+2}\) and exchange \(x\) and \(y\): \[\begin{aligned} x=\dfrac{y+1}{y+2} & \stackrel{\times (y+2)}\implies & x(y+2) =y+1 \quad \implies xy+2x= y+1\\ &\implies & xy-y=1-2x \quad \implies y(x-1)=1-2x \\ &\implies & y= \dfrac{1-2x}{x-1} \quad \implies j^{-1}(x)=\dfrac{1-2x}{x-1},\end{aligned} \nonumber \]
- Write \(y=(x-2)^2+3\) and exchange \(x\) and \(y\): \[\begin{aligned} x=(y-2)^2+3 & \implies & x-3 =(y-2)^2 \quad \implies \sqrt{x-3}=y-2\\ &\implies & y=2+\sqrt{x-3} \quad\implies k^{-1}(x)=2+\sqrt{x-3}\end{aligned} \nonumber \]
The function in the last example is not one-to-one when allowing \(x\) to be any real number. This is why we had to restrict the example to the inputs \(x\geq 2\). We exemplify the situation in the following example.
Note, that the function \(y=x^2\) can be restricted to a one-to-one function by choosing the domain to be all non-negative numbers \([0,\infty)\) or by choosing the domain to be all non-positive numbers \((-\infty,0]\).
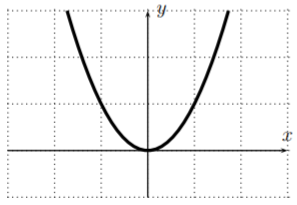
Solution
Let \(f:[0,\infty)\to [0,\infty)\) be the function \(f(x)=x^2\), so that \(f\) has a domain of all non-negative numbers. Then, the inverse is the function \(f^{-1}(x)=\sqrt{x}\).
On the other hand, we can take \(g(x)=x^2\) whose domain consists of all non-positive numbers \((-\infty,0]\), that is \(g:(-\infty,0]\to [0,\infty)\). Then, the inverse function \(g^{-1}\) must reverse domain and range, that is \(g^{-1}: [0,\infty)\to (-\infty,0]\). The inverse is obtained by exchanging \(x\) and \(y\) in \(y=x^2\) as follows:
\[x=y^2 \quad \implies y=\pm \sqrt{x}\quad \implies g^{-1}(x)=-\sqrt{x} \nonumber \]
Restrict the function to a one-to-one function. Find the inverse function, if possible.
- \(f(x)=(x+3)^2+1\)
- \(g(x)=\dfrac{1}{(x-2)^2}\)
- \(h(x)=x^3-3x^2\)
Solution
- The graph of \(f\) is displayed below.
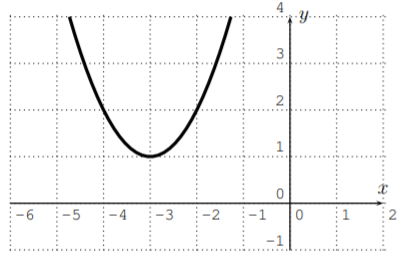
The graph shows that \(f\) is one-to-one when restricted to all numbers \(x\geq -3\), which is the choice we make to find an inverse function. Next, we replace \(x\) and \(y\) in \(y=(x+3)^2+1\) to give \(x=(y+3)^2+1\). When solving this for \(y\), we must now remember that our choice of \(x\geq -3\) becomes \(y\geq -3\) after replacing \(x\) with \(y\). We now solve for \(y\).
\[\begin{aligned} x=(y+3)^2+1 & \implies & x-1=(y+3)^2 \quad \implies y+3=\pm \sqrt{x-1} \\ & \implies & y=-3\pm \sqrt{x-1}\end{aligned} \nonumber \]
Since we have chosen the restriction of \(y\geq -3\), we use the expression with the positive sign, \(y=-3+\sqrt{x-1}\), so that the inverse function is \(f^{-1}(x)=-3+\sqrt{x-1}\).
- The graph of \(g\) is displayed below.
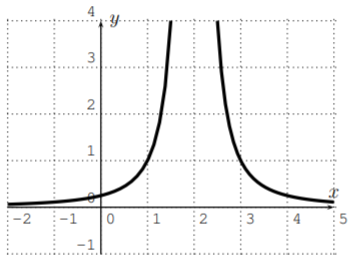
For the function \(g\), the graph shows that we can restrict \(g\) to \(x> 2\) to obtain a one-to-one function. The inverse for this choice is given as follows. Replacing \(x\) and \(y\) in \(y=\dfrac{1}{(x-2)^2}\) gives \(x=\dfrac{1}{(y-2)^2}\), which we solve this for \(y\) under the condition \(y>2\).
\[\begin{aligned} x=\dfrac{1}{(y-2)^2} & \implies & (y-2)^2=\dfrac{1}{x} \quad \implies y-2=\pm \dfrac 1 {\sqrt{x}} \\ & \implies & y=2\pm \dfrac 1 {\sqrt{x}} \quad \implies g^{-1}(x)=2+\dfrac{1}{\sqrt{x}}\end{aligned} \nonumber \]
- Finally, \(h(x)=x^3-3x^2\) can be graphed with the calculator as follows:
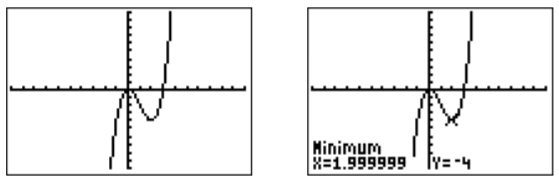
The picture on the right shows that the approximation of the local minimum is (approximately) at \(x=2\). Therefore, if we restrict \(h\) to all \(x\geq 2\), we obtain a one-to-one function. We replace \(x\) and \(y\) in \(y=x^3-3x^2\), so that the inverse function is obtained by solving the equation \(x=y^3-3y^2\) for \(y\). However, this equation is quite complicated and solving it is beyond our capabilities at this time. Therefore we simply say that \(h^{-1}(x)\) is that \(y\geq 2\) for which \(y^3-3y^2=x\), and leave the example with this.
Let \(f\) be a one-to-one function. If \(f\) maps \(x_0\) to \(y_0=f(x_0)\), then \(f^{-1}\) maps \(y_0\) to \(x_0\). In other words, the inverse function is precisely the function for which
\[\boxed{f^{-1}(f(x_0))=f^{-1}(y_0)=x_0} \quad \text{ and } \quad \boxed{f(f^{-1}(y_0))=f(x_0)=y_0} \nonumber \]
Let \(f\) and \(g\) be two one-to-one functions. Then \(f\) and \(g\) are inverses of each other exactly when
\[\boxed{f(g(x))=x}\quad \text{ and } \quad \boxed{g(f(x))=x}\quad \text{ for all }x \nonumber \]
In this case we write that \(g=f^{-1}\) and \(f=g^{-1}\).
Are the following functions inverse to each other?
- \(f(x)=5x+7, \quad g(x)=\dfrac{x-7}{5}\)
- \(f(x)=\dfrac{3}{x-6}, \quad g(x)=\dfrac{3}{x}+6\)
- \(f(x)=\sqrt{x}-3, \quad g(x)=x^2+3\)
Solution
We calculate the compositions \(f(g(x))\) and \(g(f(x))\).
- \(\begin{aligned}f(g(x)) &= f\left (\dfrac{x-7}{5}\right ) = 5\cdot\dfrac{x-7}{5}+7 = (x-7)+7 =x,\\ g(f(x)) &= g(5x+7)=\dfrac{(5x+7)-7}{5}=\dfrac{5x}{5}=x \nonumber \end{aligned}\)
- \(\begin{aligned}f(g(x)) &= f\left(\dfrac3 x +6 \right )=\dfrac{3}{(\frac{3}{x}+6)-6}=\dfrac{3}{\frac{3}{x}}=3\cdot \dfrac{x}{3}=x, \\ g(f(x)) &= \left(\dfrac{3}{x-6}\right)=\dfrac{3}{\frac{3}{x-6}}+6=3\cdot \dfrac{x-6}{3}+6=(x-6)+6=x\end{aligned} \)
Using the Observation Inverses, we see that in both part (a) and (b), the functions are inverse to each other. For part (c), we calculate for a general \(x\) in the domain of \(g\):
\[f(g(x))=\sqrt{x^2+3}-3\neq x \nonumber \]
It is enough to show that for one composition \((f\circ g)(x)\) does not equal \(x\) to conclude that \(f\) and \(g\) are not inverses. (It is not necessary to also calculate the other composition \(g(f(x))\).)
It is true that when we have one relation \(f(g(x))=x\), then we also have the other relation \(g(f(x))=x\). Nevertheless, we recommend to always check both equations. The reason is that it is easy to mistake one of the relations, when not being careful about the domain and range.
For example, let \(f(x)=x^2\) and \(g(x)=-\sqrt{x}\). Then, naively, we would calculate \(f(g(x))=(-\sqrt{x})^2=x\) and \(g(f(x))=-\sqrt{x^2}=-|x|\), so that the first equation would say \(f\) and \(g\) are inverses, whereas the second equation says they are not inverses.
We can resolve the apparent contradiction by restricting \(f\) to a one-to-one function. For example, if we take the domain of \(f\) to be all positive numbers or zero, \(D_f=[0,\infty)\), then \(f(g(x))=f(-\sqrt{x})\) which is undefined, since \(f\) only takes non-negative inputs. Also, it is \(g(f(x))=-\sqrt{x^2}=-x\). Therefore, the functions \(f\) and \(g\) are not inverse to each other!
On the other hand, if we restrict the function \(f(x)=x^2\) to all negative numbers and zero, \(D_f=(-\infty,0]\), then \(f(g(x))=(-\sqrt{x})^2=x\), since now \(f\) is defined for the negative input \(-\sqrt{x}\). Also, for a negative number \(x<0\), it is \(g(f(x))=-\sqrt{x^2}=-|x|=x\). So, in this case, \(f\) and \(g\) are inverse to each other!
Our last observation concerns the graph of inverse functions. If \(f(x_0)=y_0\) then \(f^{-1}(y_0)=x_0\), and the point \(P(x_0,y_0)\) is on the graph of \(f\), whereas the point \(Q(y_0,x_0)\) is on the graph of \(f^{-1}\).
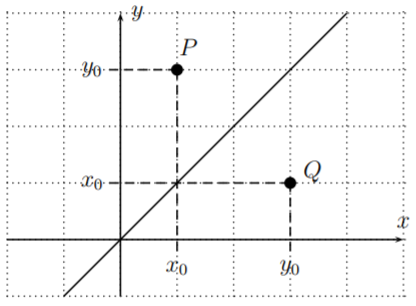
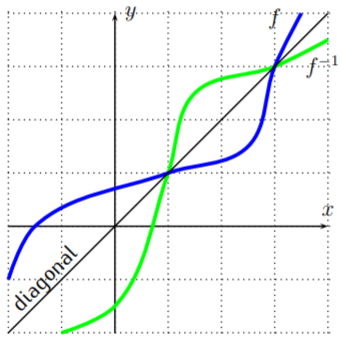
We see that \(Q\) is the reflection of \(P\) along the diagonal \(y=x\). Since this is true for any point on the graph of \(f\) and \(f^{-1}\), we have the following general observation.
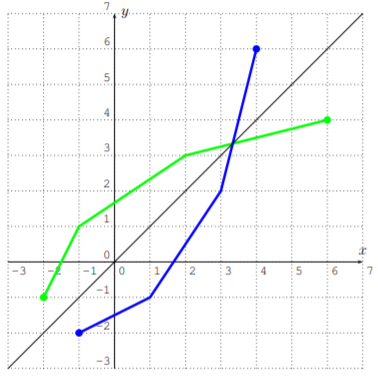
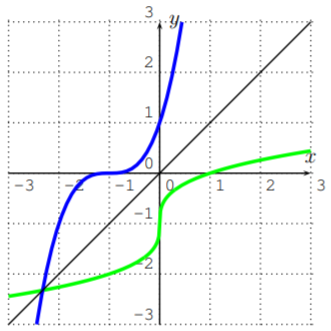
The graph of \(f^{-1}\) is the graph of \(f\) reflected along the diagonal.
Find the graph of the inverse function of the function given below.
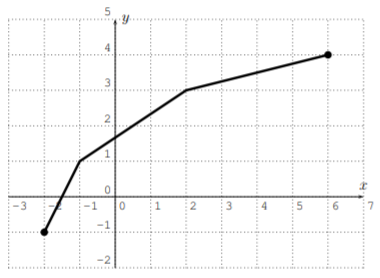
- \(f(x)=(x+1)^{3}\)
Solution
Carefully reflecting the graphs given in part (a) and (b) gives the following solution. The function \(f(x)=(x+1)^3\) in part (b) can be graphed with a calculator first.