13.2: Logarithmic functions and their graphs
- Page ID
- 49032
The logarithmic function is closely related to the exponential function. Specifically, the logarithm is the inverse function of the exponential function.
Let \(0<b\neq 1\) be a positive real number that is not equal to \(1\). For \(x>0\), the logarithm of \(x\) with base \(b\) is defined by the equivalence
\[\label{EQU:def-of-log} \boxed{ \quad y=\log_b(x) \quad\quad \Leftrightarrow \quad\quad b^y=x \quad }\]
For the particular base \(b=10\) we use the short form \[\boxed{\log(x):=\log_{10}(x)} \nonumber \]
For the particular base \(b=e\), where \(e\approx 2.71828\) is the Euler number, we call the logarithm with base \(e\) the natural logarithm, and write
\[\boxed{\ln(x):=\log_e(x)} \nonumber \]
The logarithmic function is the function \(y=\log_b(x)\) with domain \(D=\{x\in \mathbb{R} | x>0\}\) of all positive real numbers, and range \(R=\mathbb{R}\) of all real numbers. It is the inverse of the exponential function \(y=b^x\) with base \(b\).
Rewrite the equation as a logarithmic equation.
- \(3^4=81\)
- \(10^{3}=1000\)
- \(e^x=17\)
- \(2^{7\cdot a}=53\)
Solution
We can immediately apply equation \(\ref {EQU:def-of-log}\).
- For part (a), we have \(b=3\), \(y=4\), and \(x=81\). Therefore we have:
\[3^4=81 \quad \Leftrightarrow \quad \log_3(81)=4 \nonumber \]
Similarly, we obtain the solutions for (b), (c), and (d).
- \(10^3=1000\) & \(\Leftrightarrow\) & \(\log(1000)=3\)
- \(e^x=17\) & \(\Leftrightarrow\) & \(\ln(17)=x\)
- \(2^{7a}=53\) & \(\Leftrightarrow\) & \(\log_2(53)=7a\)
Evaluate the expression by rewriting it as an exponential expression.
- \(\log_2(16)\)
- \(\log_5(125)\)
- \(\log_{13}(1)\)
- \(\log_4(4)\)
- \(\log(10,000)\)
- \(\log(0.001)\)
- \(\ln(e^7)\)
- \(\log_b(b^x)\)
Solution
- If we set \(y=\log_2(16)\), then this is equivalent to \(2^y=16\). Since, clearly, \(2^4=16\), we see that \(y=4\). Therefore, we have \(\log_2(16)=4\).
- \(\begin{aligned}
\log _{5}(125)=y & \Leftrightarrow 5^{y}=125 \\
&\left(\text { since } 5^{3}=125\right)\\
&\Longrightarrow \quad 3=y=\log _{5}(125)
\end{aligned} \)
- \(\begin{aligned}
\log _{13}(1)=y & \Leftrightarrow 13^{y}=1\\
&{\left(\text { since } 13^{0}=1\right)} \\
&\Longrightarrow 0=y=\log _{13}(1)
\end{aligned}\)
- \(\begin{aligned}
\log _{4}(4)=y & \Leftrightarrow 4^{y}=4 \\
&\left(\text { since } 4^{1}=4\right) \\
&\Longrightarrow \quad 1=y=\log _{4}(4)
\end{aligned}\)
- \(\begin{aligned}
\log (100,000)=y & \Leftrightarrow \quad 10^{y}=100,000 \\
& \left(\text { since } 10^{5}=100,000\right)\\ & \Longrightarrow \quad 5=y=\log (100,000)
\end{aligned}\)
- \(\begin{aligned}
\log (0.001)=y & \Leftrightarrow \quad 10^{y}=0.001 \\
& \left(\text { since } 10^{-3}=0.001 \right )\\
&{\Longrightarrow} \quad-3=y=\log (0.001)
\end{aligned}\) - \(\ln \left(e^{7}\right)=y \quad \Leftrightarrow \quad e^{y}=e^{7} \quad \Longrightarrow \quad 7=y=\ln \left(e^{7}\right)\)
- \(\log _{b}\left(b^{x}\right)=y \quad \Leftrightarrow \quad b^{y}=b^{x} \quad \Longrightarrow \quad x=y=\log _{b}\left(b^{x}\right)\)
In the previous example (in parts (c), (d), and (h)), we were able to find certain elementary logarithms. We record these in the next observation.
We have the elementary logarithms:
\[\label{EQU:elementary-log} \boxed{\log_b(b^x) =x} \quad\quad\quad \boxed{\log_b(b)=1} \quad\quad\quad \boxed{\log_b(1)=0} \nonumber \]
In general, when the argument is not a power of the base, we can use the calculator to approximate the values of a logarithm via the formulas:
\[\label{EQU:log-change-basis-calculator} \boxed{\log_b(x) = \dfrac{\log(x)}{\log(b)}}\quad\quad\quad \text{or}\quad\quad\quad \boxed{\log_b(x) = \dfrac{\ln(x)}{\ln(b)}}\]
The last two formulas will be proved in proposition 14.1. For now, we want to show how they can be used to calculate any logarithmic expression with the calculator.
Calculate:
- \(\log_3(13)\)
- \(\log_{2.34}(98.765)\)
Solution
- We calculate \(\log_3(13)\) by using the first formula in \(\ref{EQU:log-change-basis-calculator}\).
\[\log_3(13)=\dfrac{\log(13)}{\log(3)}\approx 2.335 \nonumber \]
Alternatively, we can also calculate this with the second formula in \(\ref{EQU:log-change-basis-calculator}\).
\[\log_3(13)=\dfrac{\ln(13)}{\ln(3)}\approx 2.335 \nonumber \]
- For part (b) we have \(\log_{2.34}(98.765)=\dfrac{\log(98.765)}{\log(2.34)}\approx 5.402\).
We also want to gain an understanding of the graph of a logarithmic function. Consider the graph of \(y=2^x\) from the previous section. Recall that the graph of the inverse of a function is the reflection of the graph of the function about the diagonal line \(y=x\). So in this case we have:
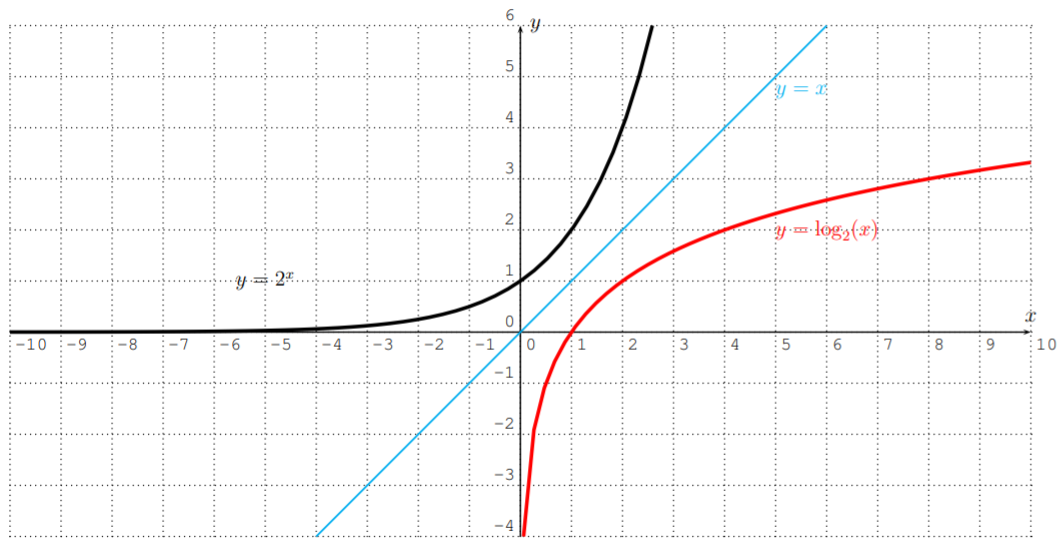
The graph can also be obtained using a graphing calculator.
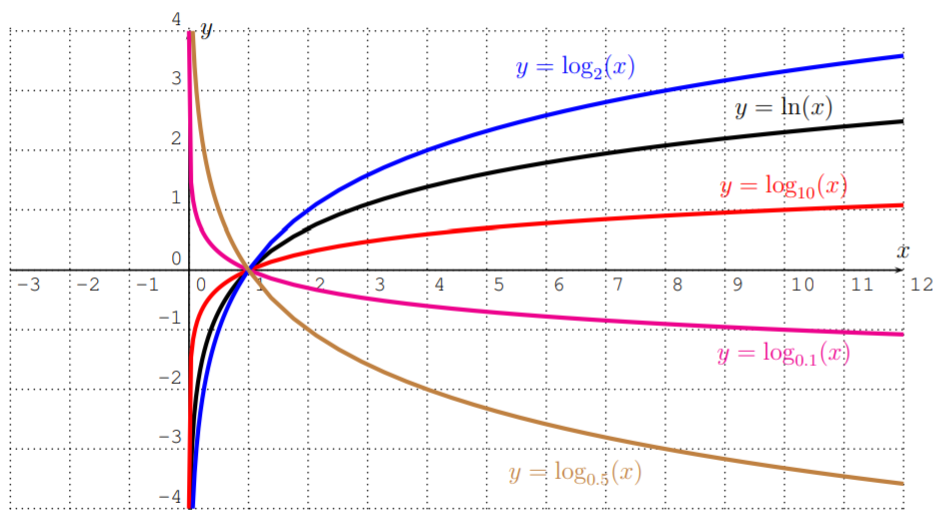
- Graph the functions \(f(x)=\ln(x)\), \(g(x)=\log(x)\), \(h(x)=\log_2(x)\), and \(k(x)=\log_{0.5}(x)\). What are the domains of \(f\), \(g\), \(h\), and \(k\)? How do these functions differ?
- Graph the function \(p(x)= -3\cdot \ln(x)+4\). What is the domain of \(p\)?
- Graph the function \(q(x)= \ln(5-x)\). What is the domain of \(q\)?
- Graph the function \(r(x)= \log_7(2x+8)\). What is the domain of \(r\)?
Solution
- We know from the definition that the domain of \(f\), \(g\), and \(h\) is all real positive numbers, \(D_f=D_g=D_h=D_k=\{x|x>0\}\). The functions \(f\) and \(g\) can immediately be entered into the calculator. The standard window gives the following graphs.
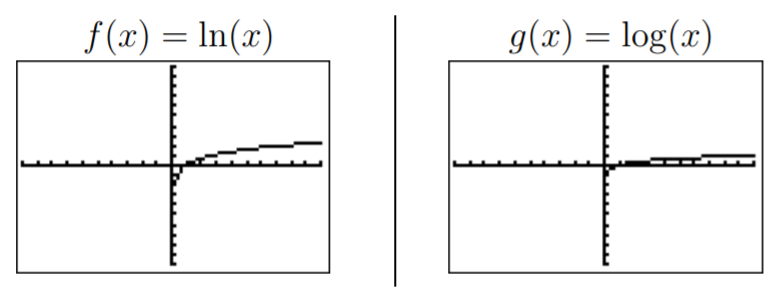
Note that we can rewrite \(g(x)\), \(h(x)\), and \(k(x)\) as a constant times \(f(x)\):
\[\begin{aligned} g(x)&= \log(x)=\log_{10}(x)=\dfrac{\ln(x)}{\ln(10)}=\dfrac{1}{\ln(10)}\cdot f(x) \\ h(x)&= \log_{2}(x)=\dfrac{\ln(x)}{\ln(2)}=\dfrac{1}{\ln(2)}\cdot f(x) \\ k(x)&= \log_{0.5}(x)=\dfrac{\ln(x)}{\ln(0.5)}=\dfrac{1}{\ln(0.5)}\cdot f(x) \end{aligned} \nonumber \]
Since \(\dfrac{1}{\ln(10)}\approx 0.434<1\), we see that the graph of \(g\) is that of \(f\) compressed towards the \(x\)-axis by a factor \(\dfrac{1}{\ln(10)}\). Similarly, \(\dfrac{1}{\ln(2)}\approx 1.443>1\), so that the graph of \(h\) is that of \(f\) stretched away from the \(x\)-axis by a factor \(\dfrac{1}{\ln(2)}\). Finally, \(\dfrac{1}{\ln(0.5)}\approx -1.443\), or more precisely, \(\dfrac{1}{\ln(0.5)}=\dfrac{1}{\ln(2^{-1})}=-\dfrac{1}{\ln(2)}\), so that the graph of \(k\) is that of \(h\) reflected about the \(x\)-axis.
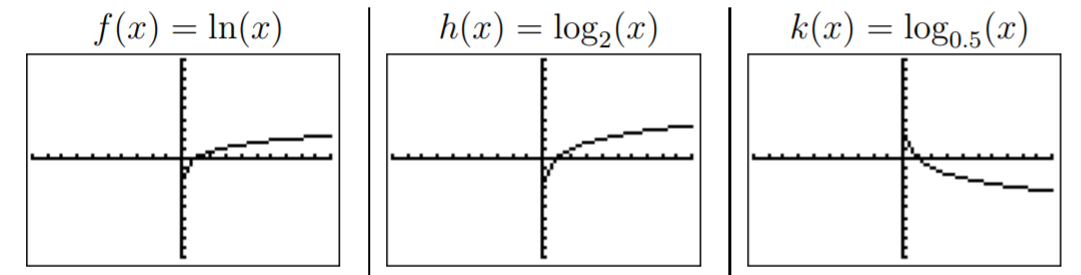
Note that all these graphs have a common \(x\)-intercept at \(x=1\):
\[f(1)=g(1)=h(1)=k(1)=0 \nonumber \]
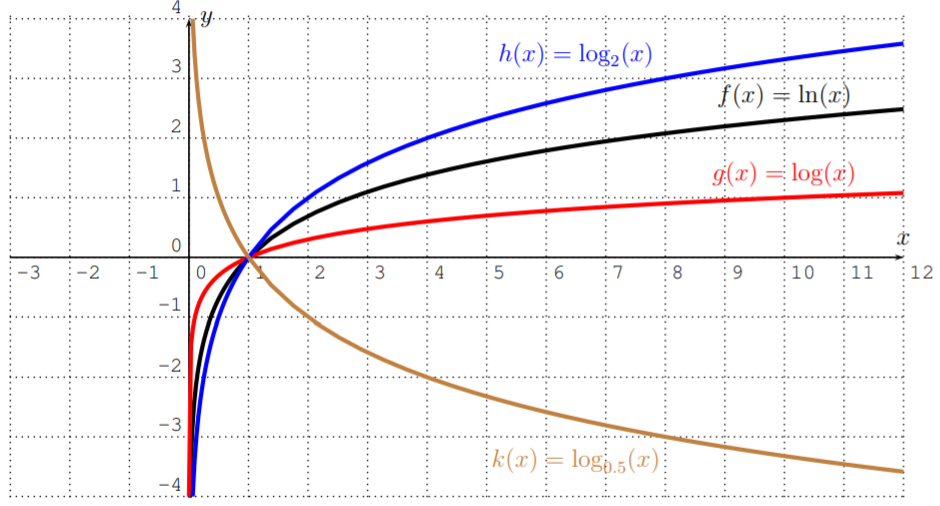
To visualize the differences between the graphs, we graph them together in one coordinate system.
- Using our knowledge of transformations of graphs, we expect that \(p(x)=-3\cdot \ln(x)+4\) is that of \(y=\ln(x)\) reflected and stretched away from the \(x\)-axis (by a factor \(3\)), and then shifted up by \(4\). The stretched and reflected graph is in the middle below, whereas the graph of the shifted function \(p\) is on the right below.
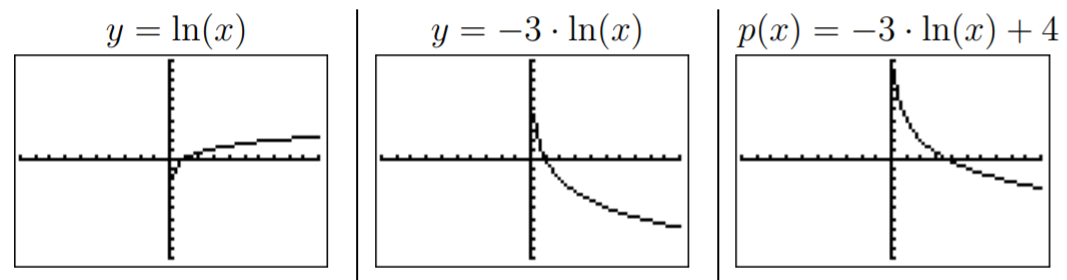
The domain consist of numbers \(x\) for which the \(\ln(x)\) is defined, that is, \(D_p=\{x|x>0\}\).
- To determine the domain of \(q(x)=\ln(5-x)\), we have to see for which \(x\) the logarithm has a positive argument. More precisely, we need \(5-x>0\), that is, \(5>x\), so that the domain is \(D_q=\{x|x<5\}\). The calculator displays the following graph.
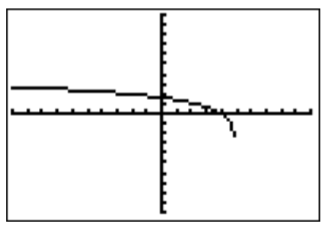
Note that the graph, as displayed by the calculator, appears to end at a point that is approximately at \((5,-2.5)\). However, the actual graph of the logarithm does not stop at any point, since it has a vertical asymptote at \(x=5\), that is, the graph approaches \(-\infty\) as \(x\) approaches \(5\). The calculator only displays an approximation, which may be misleading since this approximation is determined by the window size and the size of each pixel. The graph would therefore look as follows.
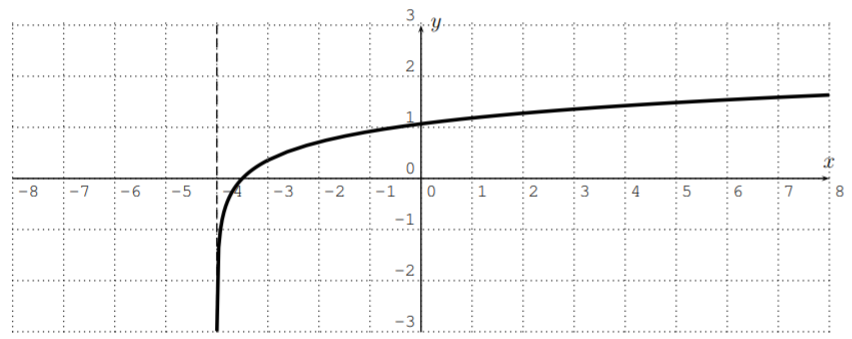
- The domain of \(r(x)= \log_7(2x+8)\) consists of those numbers \(x\) for which the argument of the logarithm is positive.
\[2x+8>0 \stackrel{\text{(subtract $8$)}}\implies \quad 2x>-8 \stackrel{\text{(divide by $2$)}}\implies \quad x>-4 \nonumber \]
Therefore, the domain is \(D_r=\{x|x>-4\}\). To graph the function \(r(x)= \log_7(2x+8)\), we can enter \(r(x)=\dfrac{\ln(2x+8)}{\ln(7)}\) into the calculator. The graph looks as follows.
The previous example analyzes the graph of the logarithm function. Here is the summary.
The graph of a logarithmic function \(y=\log_b(x)\) with base \(b\) is that of the natural logarithm \(y=\ln(x)\) stretched away from the \(x\)-axis, or compressed towards the \(x\)-axis when \(b>1\). When \(0<b<1\), the graph is furthermore reflected about the \(x\)-axis.
The graph \(y=\log_b(x)\) has domain \(D=\{x|x>0\}\), and a vertical asymptote at \(x=0\). There is no horizontal asymptote, as \(f(x)\) approaches \(+\infty\) when \(x\) approaches \(+\infty\) for \(b>1\), and \(f(x)\) approaches \(-\infty\) when \(x\) approaches \(+\infty\) for \(0<b<1\). Finally, there is an \(x\)-intercept at \(x=1\).