17.1: Basic trigonometric definitions and facts
- Page ID
- 49059
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this part, we will investigate trigonometric functions, such as \(y=\sin(x)\), \(y=\cos(x)\), and \(y=\tan(x)\) in terms of their function theoretic aspects. Before we graph these functions, we recall the basic definitions and the main facts, which we will consider as known background material.
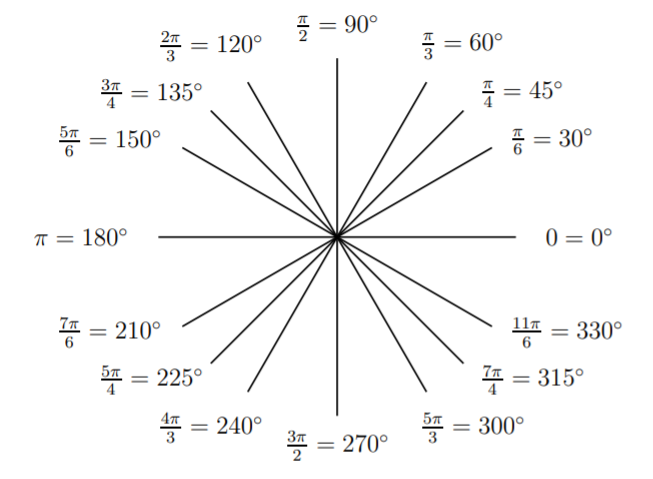
An angle can be expressed in degree or in radian measure. The relationship between degrees and radians is given by
\[\boxed{\pi=180^\circ} \nonumber \]
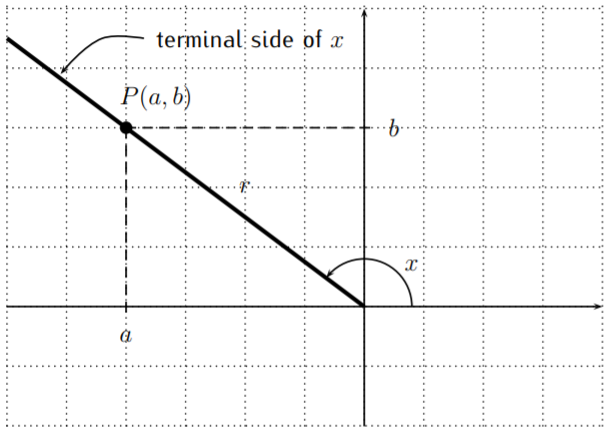
Let \(x\) be an angle. Consider the terminal side of the angle \(x\), and assume that the point \(P(a,b)\) is a point on the terminal side of \(x\). If \(r\) is the distance from \(P\) to the origin \((0,0)\), then we define the sine, cosine, tangent, cosecant, secant, and cotangent as follows:
\[\boxed {\begin{aligned}
& a^{2}+b^{2}=r^{2} \\
\implies & r=\sqrt{a^{2}+b^{2}}
\end{aligned}} \nonumber \]
\[\boxed {\begin{array}{ll}
\sin (x)=\dfrac{b}{r} & \csc (x)=\dfrac{r}{b} \\
\cos (x)=\dfrac{a}{r} & \sec (x)=\dfrac{r}{a} \\
\tan (x)=\dfrac{b}{a} & \cot (x)=\dfrac{a}{b}
\end{array}} \nonumber \]
There are some immediate consequences from the above definition.
\[\begin{aligned} \boxed{\csc(x)=\dfrac{1}{\sin(x)}} && \boxed{\sec(x)=\dfrac{1}{\cos(x)}} \\ \boxed{\tan(x)=\dfrac{\sin(x)}{\cos(x)}} && \boxed{\cot(x)=\dfrac{\cos(x)}{\sin(x)}=\dfrac{1}{\tan(x)}}\end{aligned}\]
If we take \(r=1\) in the above we have the following ‘unit circle’ definition of \(\sin\) and \(\cos\):
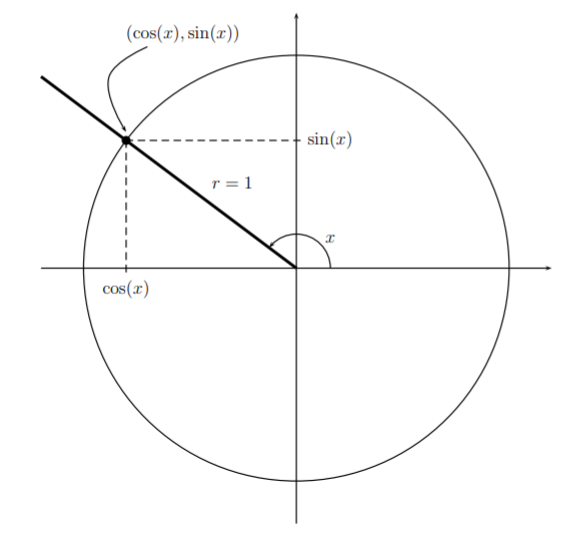
That is to say, that the point where the terminal side of the angle \(x\) intersects the unit circle is \((\cos(x),\sin(x))\) (which can serve as a definition \(\cos\) and \(\sin\) as functions of \(x\)).
For the following, we use the short hand notation:
\[\sin^2\alpha:=(\sin \alpha)^2, \quad \cos^2\alpha:=(\cos \alpha)^2 , \quad\text{ and }\quad \tan^2\alpha:=(\tan \alpha)^2 \nonumber \]
From these definitions, we obtain that
\[\label{EQU:sin2+cos2=1} \boxed{\sin^2(x)+\cos^2(x)=1} \quad \quad \boxed{\sec^2(x)=1+\tan^2(x)}\]
since \(\sin^2(x)+\cos^2(x)=\left(\dfrac{b}{r}\right)^2+\left(\dfrac{a}{r}\right)^2=\dfrac{b^2+a^2}{r^2}=\dfrac{r^2}{r^2}=1\), and, similarly, \(1+\tan^2(x)=1+\left(\dfrac{b}{a}\right)^2=\dfrac{a^2+b^2}{a^2}=\dfrac{r^2}{a^2}=\left(\dfrac{r}{a}\right)^2=\sec^2(x)\). Furthermore, we can see from the definition that
\[\label{EQU:basic-trig-eqns-wrt-pi} \begin{matrix} \boxed{\sin(x+2\pi)=\sin(x)}&\boxed{\sin(-x)=-\sin(x)}&\boxed{\sin(\pi-x)=\sin(x)}\\&&\\ \boxed{\cos(x+2\pi)=\cos(x)}&\boxed{\cos(-x)=\cos(x)}&\boxed{\cos(\pi-x)=-\cos(x)} \end{matrix} \]
For a point \(P(a,b)\) the \(x\)-coordinate \(a\) is positive when \(P\) is in quadrant I and IV, whereas the \(y\)-coordinate \(b\) is positive when \(P\) is in quadrant I and II. The length of the hypothenuse \(r\) is always positive. Thus the trigonometric functions are positive/negative according to the chart:
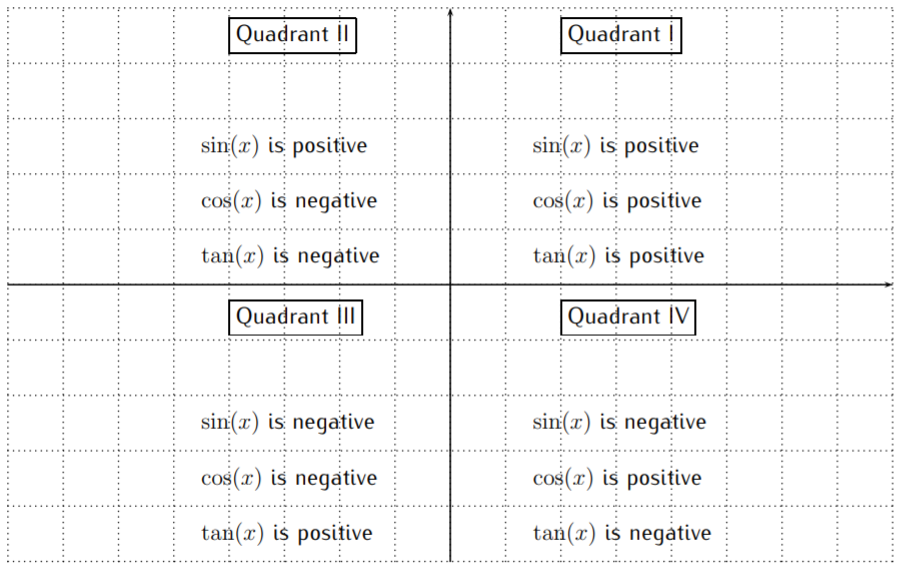
There are two basic triangles that are used to calculate exact values of the trigonometric functions. These two triangles are the \(45^\circ-45^\circ-90^\circ\) and \(30^\circ-60^\circ-90^\circ\) triangles, which can be described with specific side lengths.
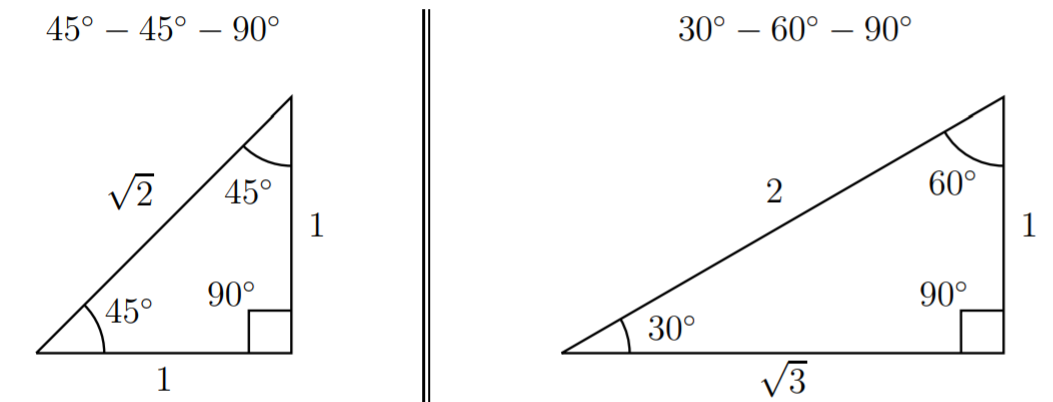
These basic triangles may be used to calculate the trigonometric functions of certain angles.
Find \(\sin(x)\), \(\cos(x)\), and \(\tan(x)\) for the angles
\[x=30^\circ,\quad x=45^\circ, \quad x=60^\circ,\quad x=90^\circ,\quad x=0^\circ \nonumber \]
Solution
We draw the angle \(x=30^\circ\) in the plane, and use the special triangle to find a point on the terminal side of the angle. From this, we then read off the trigonometric functions. Here are the function values for \(30^\circ\), \(45^\circ\), and \(60^\circ\).
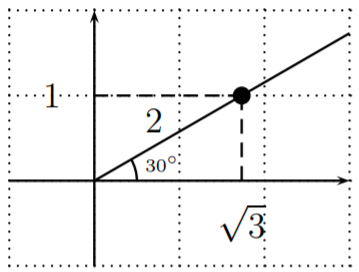
\sin \left(30^{\circ}\right)&=\dfrac{b}{r}=\dfrac{1}{2} \\
\cos \left(30^{\circ}\right)&=\dfrac{a}{r}=\dfrac{\sqrt{3}}{2} \\
\tan \left(30^{\circ}\right)&=\dfrac{b}{a}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}
\end{aligned} \)
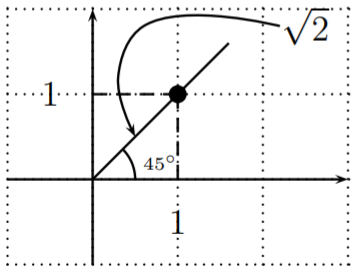
\sin \left(45^{\circ}\right)&=\dfrac{b}{r}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2} \\
\cos \left(45^{\circ}\right)&=\dfrac{a}{r}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2} \\
\tan \left(45^{\circ}\right)&=\dfrac{b}{a}=\dfrac{1}{1}=1
\end{aligned}\)
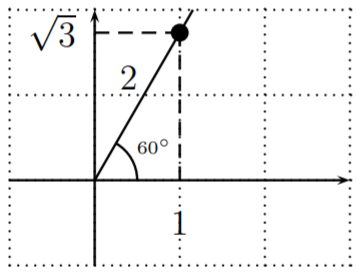
\sin \left(60^{\circ}\right)&=\dfrac{b}{r}=\dfrac{\sqrt{3}}{2} \\
\cos \left(60^{\circ}\right)&=\dfrac{a}{r}=\dfrac{1}{2} \\
\tan \left(60^{\circ}\right)&=\dfrac{b}{a}=\dfrac{\sqrt{3}}{1}=\sqrt{3}
\end{aligned}\)
Here are the trigonometric functions for \(90^\circ\) and \(0^\circ\).
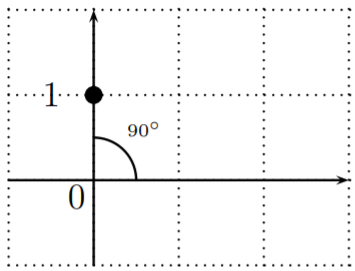
\sin \left(90^{\circ}\right)&=\dfrac{b}{r}=\dfrac{1}{1}=1 \\
\cos \left(90^{\circ}\right)&=\dfrac{a}{r}=\dfrac{0}{1}=0 \\
\tan \left(90^{\circ}\right)&=\dfrac{b}{a}=\dfrac{1}{0} \quad \text{is undefined}
\end{aligned}\)
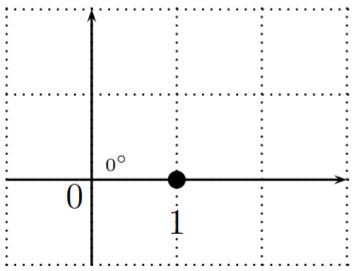
\sin \left(0^{\circ}\right)&=\dfrac{b}{r}=\dfrac{0}{1}=0 \\
\cos \left(0^{\circ}\right)&=\dfrac{a}{r}=\dfrac{1}{1}=1 \\
\tan \left(0^{\circ}\right)&=\dfrac{b}{a}=\dfrac{0}{1}=0
\end{aligned}\)
We collect the results of the previous example in a table:
\[\begin{array}{c||c|c|c|c|c}
x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\
\hline \hline \sin (x) & 0 & \dfrac{1}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & 1 \\
\hline \cos (x) & 1 & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{1}{2} & 0 \\
\hline \tan (x) & 0 & \dfrac{\sqrt{3}}{3} & 1 & \sqrt{3} & \text { undef. }
\end{array} \nonumber \]
There is an easy way to remember the function value given in the above table by writing the numerator of \(\sin(x)\) as \(\sqrt{0}, \sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}\) in increasing order, and for \(\cos(x)\) in decreasing order:
\[\begin{array}{c|c|c|c|c|c}
x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\
\hline \sin (x) & \dfrac{\sqrt{0}}{2} & \dfrac{\sqrt{1}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{4}}{2} \\
\hline \cos (x) & \dfrac{\sqrt{4}}{2} & \dfrac{\sqrt{3}}{2} & \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{1}}{2} & \dfrac{\sqrt{0}}{2}
\end{array} \nonumber \]
The values of \(\tan(x)\) are then determined from this by \(\tan (x)=\dfrac{\sin (x)}{\cos (x)}\):
\[\begin{array}{c|c|c|c|c|c}
x & 0=0^{\circ} & \dfrac{\pi}{6}=30^{\circ} & \dfrac{\pi}{4}=45^{\circ} & \dfrac{\pi}{3}=60^{\circ} & \dfrac{\pi}{2}=90^{\circ} \\
\hline \tan (x) & \dfrac{0}{1}=0 & \dfrac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} & \dfrac{\sqrt{2}}{\frac{\sqrt{2}}{2}}=1 & \dfrac{\sqrt{3}}{\frac{1}{2}}=\sqrt{3} & {}'' \dfrac{1}{0} {}'' \text { is undef. }
\end{array} \nonumber \]
We can use the special \(45^\circ-45^\circ-90^\circ\) and \(30^\circ-60^\circ-90^\circ\) triangles to also find other values of the trigonometric functions.
Find \(\sin(x)\), \(\cos(x)\), and \(\tan(x)\) for the following angles.
- \(x=240^\circ\)
- \(x=495^\circ\)
- \(x=\dfrac{11\pi}{6}\)
- \(x=\dfrac{-9\pi}{4}\)
Solution
- We graph the angle \(x=240^\circ\), and identify a special \(30^\circ-60^\circ-90^\circ\) triangle using the terminal side of \(x\).
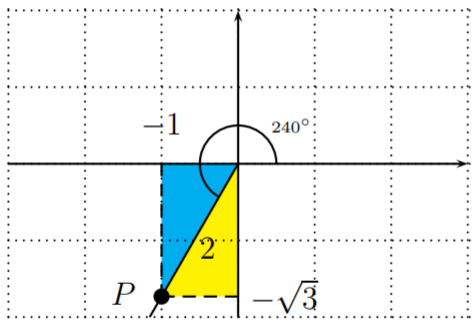
We identify a point \(P\) on the terminal side of \(x\). This point \(P\) has coordinates \(P(-1,-\sqrt{3})\), which can be seen by considering one of two \(30^\circ-60^\circ-90^\circ\) triangles in the plane (shaded above). The length of the line segment from \(P\) to the origin \((0,0)\) is \(2\). Thus, \(a=-1, b=-\sqrt{3}, r=2\). We get
\[\sin(240^\circ)=\dfrac{-\sqrt{3}}{2}, \quad \cos(240^\circ)=\dfrac{-1}{2},\quad \tan(240^\circ)=\dfrac{-\sqrt{3}}{-1}=\sqrt{3} \nonumber \]
- The angle \(x=495^\circ\) is greater than \(360^\circ\). However, the trigonometric functions are invariant under addition or subtraction of \(360^\circ\):
\[\boxed{\sin(x\pm 360^\circ)=\sin(x)} \,\,\, \boxed{\cos(x\pm 360^\circ)=\cos(x)} \,\,\, \boxed{\tan(x\pm 360^\circ)=\tan(x)} \nonumber \]
Since \(495^\circ-360^\circ=135^\circ\), we have \(\sin(495^\circ)=\sin(135^\circ)\), and similarly for \(\cos\) and \(\tan\). Graphing the terminal side of \(x\), and identifying a special \(45^\circ-45^\circ-90^\circ\) triangle, we find the coordinates of a point \(P\) on the terminal side with coordinates \(P(-1,1)\).
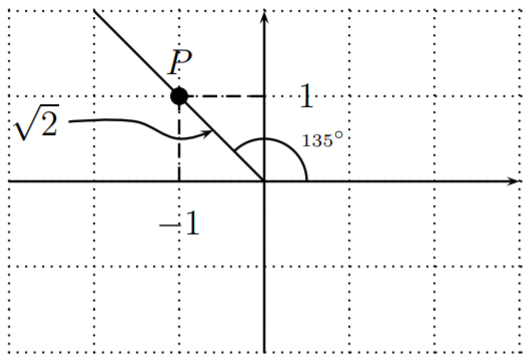
Therefore, \(a=-1, b=1, r=\sqrt{2}\). We obtain
\[\sin(495^\circ)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}, \quad \cos(495^\circ)=\dfrac{-1}{\sqrt{2}}=\dfrac{-\sqrt{2}}{2},\quad \tan(495^\circ)=\dfrac{1}{-1}=-1 \nonumber \]
- Converting \(\dfrac{11\pi}{6}\) into degrees, we have
\[x=\dfrac{11\pi}{6}=\dfrac{11\pi}{6}\cdot \dfrac{180^\circ}{\pi}=11\cdot 30^\circ=330^\circ \nonumber \]
Drawing the terminal side, we obtain the point \(P\).
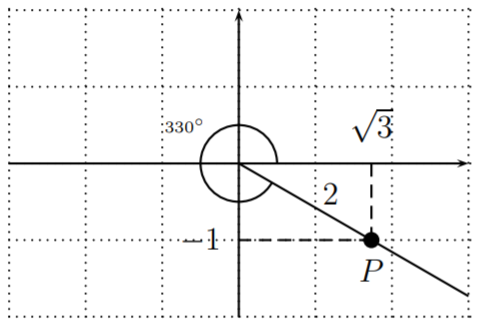
The point \(P\) has coordinates \(P(\sqrt{3},-1)\). Therefore, \(a=\sqrt{3}, b=-1, r=2\), and
\[\sin\Big(\dfrac{11\pi}{6}\Big)=\dfrac{-1}{2}, \quad \cos\Big(\dfrac{11\pi}{6}\Big)=\dfrac{\sqrt{3}}{2},\quad \tan\Big(\dfrac{11\pi}{6}\Big)=\dfrac{-1}{\sqrt{3}}=\dfrac{-\sqrt{3}}{3} \nonumber \]
- Converting the angle \(x=\dfrac{-9\pi}{4}=\dfrac{-9\pi}{4}\cdot \dfrac{180^\circ}{\pi}=-9\cdot 45^\circ=-405^\circ\), we see that the trigonometric functions of \(x\) are the same as of \(-405^\circ+360^\circ=-45^\circ\), and also of \(-45^\circ+360^\circ=315^\circ\). We can draw either \(-45^\circ\) or \(315^\circ\) to find a point \(P\) on the terminal side of \(x\).
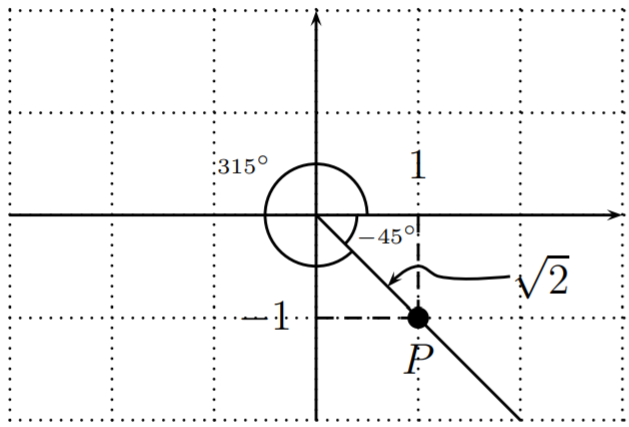
The point \(P(1,-1)\) determines \(a=1, b=-1, r=\sqrt{2}\), and so
\[\begin{aligned} && \sin\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{-1}{\sqrt{2}}=\dfrac{-\sqrt{2}}{2}, \quad \cos\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}, \\ && \tan\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{-1}{1}=-1 \end{aligned} \nonumber \]


