21.1: Polar Form of Complex Numbers

We now recall the definition of complex numbers and show how they are represented on the complex plane.

Definition: Imaginary or Complex unit

We define the imaginary unit or complex unit to be

\[\label{DEF:imaginary-unit} \text{imaginary unit: } \boxed{i=\sqrt{-1}} \nonumber \]

In other words, \(i\) is a solution of the equation:

\[\boxed{i^2=-1} \nonumber \]

Definition: Complex number

A complex number is a number of the form \(a+b\cdot i\). (Alternatively we also write this as \(a+bi\) without the dot for the multiplication.) Here \(a\) and \(b\) are any real numbers. The number \(a\) is called the real part of \(a+b\cdot i\), and \(b\) is called the imaginary part of \(a+b\cdot i\). The set of all complex numbers is denoted by \(\mathbb{C}\).

Here are some examples of complex numbers:

\[3+2i, \quad 1-1\cdot i, \quad \sqrt{2}+\pi \cdot i, \quad 5+0\cdot i, \quad 0+3\cdot i \nonumber \]

Note that in the last two examples, we have \(5+0\cdot i=5\), so that we see that the real number \(5\) is also a complex number. Indeed, any real number \(a=a+0\cdot i\) is also a complex number. Similarly, \(0+3\cdot i=3i\) as well as any multiple of \(i\) is also a complex number (these numbers are often called pure imaginary numbers).

In analogy to section 1.1, where we represented the real numbers on the number line, we can represent the complex numbers on the complex plane:

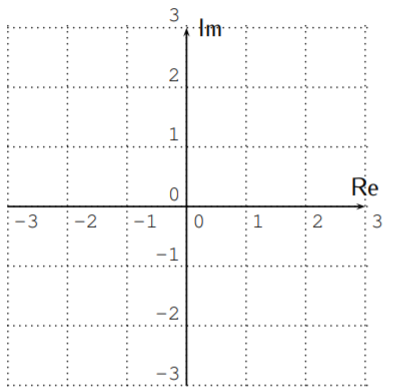
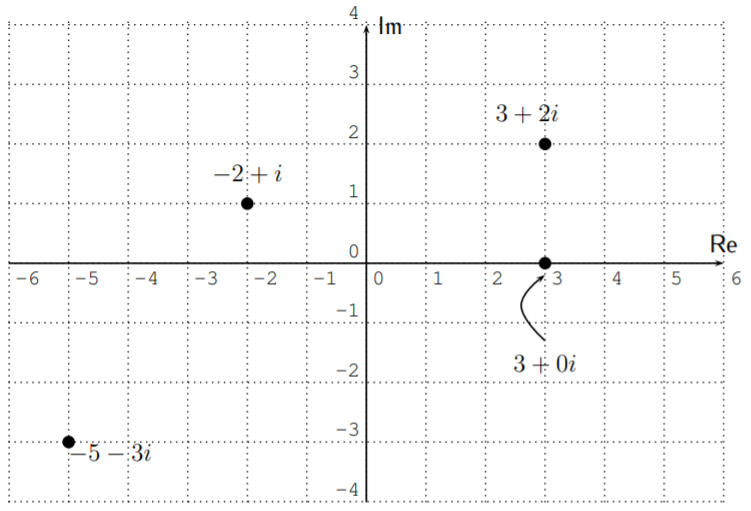
The complex number \(a+bi\) is represented as the point with coordinates \((a,b)\) in the complex plane.

Example \(\PageIndex{1}\)

Perform the operation.

1. \((2-3i)+(-6+4i)\)
2. \((3+5i)\cdot (-7+i)\)
3. \(\dfrac{5+4i}{3+2i}\)

Solution

1. Adding real and imaginary parts, respectively, gives,

\[(2-3i)+(-6+4i) = 2-3i-6+4i = -4+i \nonumber \]

2. We multiply (using FOIL), and use that \(i^2=-1\).

\[\begin{aligned} (3+5i)\cdot (-7+i) &=-21+3i-35i+5i^2\\&=-21-32i+5\cdot(-1)\\ &=-21-32i-5\\&=-26-32i\end{aligned} \nonumber \]

3. Recall that we may simplify a quotient of complex numbers by multiplying numerator and denominator by the conjugate of the denominator.

\[\begin{aligned} \dfrac{5+4i}{3+2i} &= \dfrac{(5+4i)\cdot (3-2i)}{(3+2i)\cdot (3-2i)}\\& =\dfrac{15-10i+12i-8i^2}{9-6i+6i-4i^2}\\ &= \dfrac{15+2i+8}{9+4}\\&=\dfrac{23+2i}{13}\\&=\dfrac{23}{13}+\dfrac{2}{13}i\end{aligned} \nonumber \]

The real part of the solution is \(\dfrac{23}{13}\); the imaginary part is \(\dfrac{2}{13}\).

There is also a notion of absolute value \(|a+bi|\) for any complex number \(a+bi\).

Definition: Absolute value

Let \(a+bi\) be a complex number. The absolute value of \(a+bi\), denoted by \(|a+bi|\) is the length between the point \(a+bi\) in the complex plane and the origin \((0,0)\).

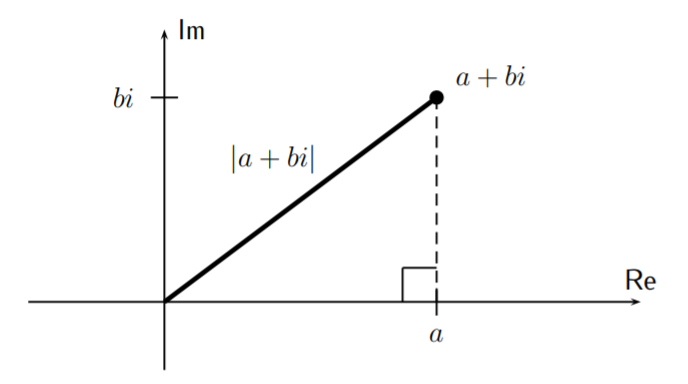
Using the Pythagorean theorem, we can calculate \(|a+bi|\) as

\[|a+bi|^2=a^2+b^2 \nonumber \]

so that

\[\boxed{ |a+bi|= \sqrt{a^2+b^2} } \nonumber \]

Example \(\PageIndex{2}\)

Find the absolute value of the complex numbers below.

1. \(5-3i\)
2. \(-8+6i\)
3. \(7i\)

Solution

The absolute values are calculated as follows.

1. \(|5-3 i|=\sqrt{5^{2}+(-3)^{2}}=\sqrt{25+9}=\sqrt{34}\)
2. \(|-8+6 i|=\sqrt{(-8)^{2}+6^{2}}=\sqrt{64+36}=\sqrt{100}=10\)
3. \(|7 i|=\sqrt{0^{2}+(7)^{2}}=\sqrt{0+49}=7\)

We can write a complex number in the form \(a+bi\), or alternatively, we may use the absolute value and “angle” to write the number in the so-called polar form, which we discuss now.

Observation: Polar form

Let \(a+bi\) be a complex number. The coordinates in the plane can be expressed in terms of the absolute value \(r=|a+bi|\) and the angle \(\theta\) with the real axis as shown below.

From the right triangle as shown in the complex plane above, we see that the coordinates \(a\) and \(b\) in the plane are given by:

\[\label{EQU:a-and-b-in-complex-number} a=r\cdot \cos(\theta)\quad\text{ and }\quad b=r\cdot \sin(\theta) \]

Therefore, the complex number is \(a+bi = r\cdot \cos(\theta) + r\cdot \sin(\theta)\cdot i\), or factoring \(r\) from this expression:

\[\boxed{a+bi = r\cdot \big(\cos(\theta)+i\cdot \sin(\theta)\big)} \]

Writing the complex number in this way is called the polar form of the complex number. Here, the number \(r\) is the absolute value, and \(\theta\) is given by \(\ref{EQU:a-and-b-in-complex-number}\) via the calculation \(\dfrac{b}{a}=\dfrac{r\cdot \sin(\theta)}{r\cdot \cos(\theta)}=\dfrac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)\). Thus,

\[\label{EQU:r-and-theta} \boxed{r=\sqrt{a^2+b^2}} \quad\text{ and }\quad \boxed{\tan(\theta)=\dfrac{b}{a}}\]

When finding the directional angle \(\theta\) of a complex number via equation \(\ref{EQU:r-and-theta}\), we have to remember that \(\tan(\theta)\) may be obtained by the two angles \(\theta\) and \(\pi+\theta\); that is, we have

\[\tan(\pi+\theta)=\tan(\theta) \nonumber \]

Therefore, we need to check that our answer for \(\theta\) lies in the correct quadrant. This is shown in the next example.

Example \(\PageIndex{3}\)

Convert the complex number to polar form.

1. \(2+3i\)
2. \(-2-2\sqrt{3}i\)
3. \(4-3i\)
4. \(-4i\)

Solution

1. First, the absolute value is \(r=|2+3i|=\sqrt{2^2+3^2}=\sqrt{13}\). Furthermore, since \(a=2\) and \(b=3\), we have \(\tan(\theta)=\dfrac{3}{2}\). To obtain \(\theta\), we calculate

\[\tan^{-1}\Big(\dfrac{3}{2}\Big)\approx 56.3^\circ \nonumber \]

Note that \(56.3^\circ\) is in the first quadrant, and so is the complex number \(2+3i\)

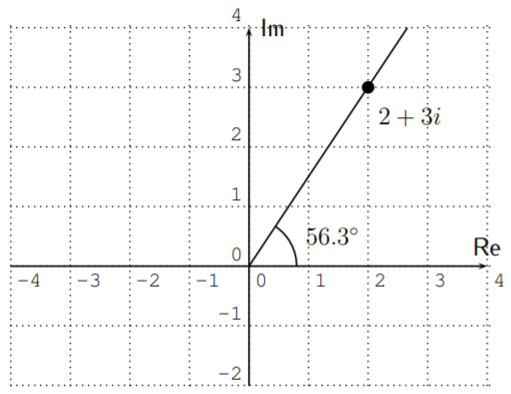
Therefore, \(\theta\approx 56.3^\circ\), and we obtain our answer:

\[2+3i\approx \sqrt{13}\cdot \left(\cos(56.3^\circ)+i\sin(56.3^\circ)\right) \nonumber \]

2. For \(-2-2\sqrt{3}i\), we first calculate the absolute value:

\[r=\sqrt{(-2)^2+(-2\sqrt{3})^2}=\sqrt{4+4\cdot 3}=\sqrt{4+12}=\sqrt{16}=4 \nonumber \]

Furthermore, \(\tan(\theta)=\dfrac{b}{a}=\dfrac{-2\sqrt{3}}{-2}=\sqrt{3}\). Now, \(\tan^{-1}(\sqrt{3})=60^\circ=\dfrac{\pi}{3}\). However, graphing the angle \(\dfrac{\pi}{3}=60^\circ\) and the number \(-2-2\sqrt{3}i\), we see that \(60^\circ\) is in the first quadrant, whereas \(-2-2\sqrt{3}i\) is in the third quadrant.

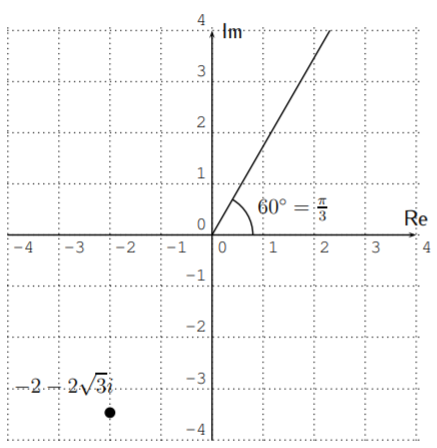
Therefore, we have to add \(\pi\) to \(\dfrac \pi 3\) to get the correct angle for \(-2-2\sqrt{3} i\), that is \(\theta=\dfrac{\pi}{3}+\pi=\dfrac{\pi+3\pi}{3}=\dfrac{4\pi}{3}\). Our complex number in polar form is

\[-2-2\sqrt{3}i = 4\cdot \left(\cos\left(\dfrac{4\pi}{3}\right)+i\sin\left(\dfrac{4\pi}{3}\right)\right) \nonumber \]

3. For \(4-3i\) we calculate \(r=\sqrt{4^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5\). The angle \(\tan^{-1}\left(\dfrac{-3}{4}\right)\approx -36.9^\circ\), which is in the fourth quadrant, just like the number \(4-3i\).

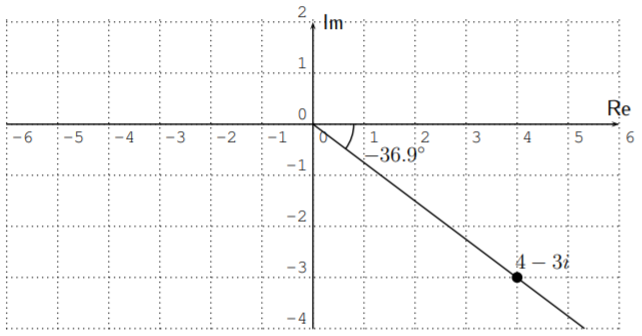
Therefore, \(\theta\approx-36.9^\circ\), and we write

\[4-3i\approx 5\cdot (\cos(-36.9^\circ)+i\sin(-36.9^\circ)) \nonumber \]

4. We calculate the absolute value of \(0-4i\) as \(r=\sqrt{0^2+(-4)^2}=\sqrt{16}=4\). However, when calculating the angle \(\theta\) of \(0-4i\), we are lead to consider \(\tan^{-1}\left(\dfrac{-4}{0}\right)\), which is undefined! The reason for this can be seen by plotting the number \(-4i\) in the complex plane.

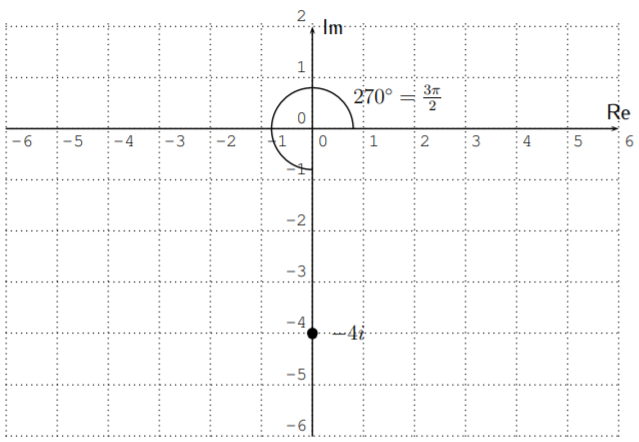
The angle \(\theta=270^\circ\) (or alternatively \(\theta=-90^\circ\)), so that the complex number is

\[\begin{aligned} -4i &= 4\cdot (\cos(270^\circ)+i\sin(270^\circ)) \\ &= 4\cdot \left(\cos\left(\dfrac{3\pi}{2}\right)+i\sin\left(\dfrac{3\pi}{2}\right)\right) \end{aligned} \nonumber \]

Note that we may write our answer either in degree or radian mode as we did above.

We may also perform the reverse conversion of a complex number from polar form into “standard form” \(a+bi\).

Example \(\PageIndex{4}\)

Convert the number from polar form into the standard form \(a+bi\).

1. \(3\cdot (\cos(117^\circ)+i\sin(117^\circ))\)
2. \(4\cdot \left(\cos\left(\dfrac{5\pi}{4}\right)+i\sin\left(\dfrac{5\pi}{4}\right)\right)\)

Solution

1. Since we don’t have an exact formula for \(\cos(117^\circ)\) or \(\sin(117^\circ)\), we use the calculator to obtain approximate values.

\[3\cdot (\cos(117^\circ)+i\sin(117^\circ))\approx 3\cdot (-0.454+i \cdot 0.891)=-1.362+2.673 i \nonumber \]

2. We recall that \(\cos\left(\dfrac{5\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\) and \(\sin\left(\dfrac{5\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\). (This can be seen as in Example 17.1.2 by considering the point \(P(-1,-1)\) on the terminal side of the angle \(\dfrac{5\pi}{4}=\dfrac{5\cdot 180^\circ}{4}=225^\circ\).

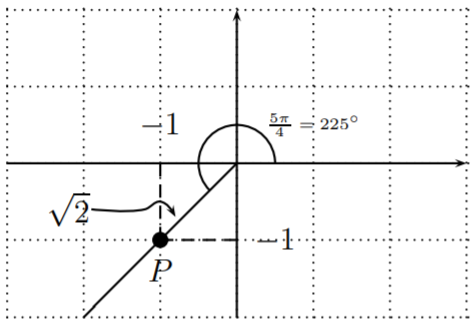
Therefore, \(\cos\left(\dfrac{5\pi}{4}\right)=\dfrac{-1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\) and \(\sin\left(\dfrac{5\pi}{4}\right)=\dfrac{-1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).

With this, we obtain the complex number in standard form.

\[\begin{aligned} 4\cdot \left(\cos\left(\dfrac{5\pi}{4}\right)+i\sin\left(\dfrac{5\pi}{4}\right)\right) &= 4\cdot \left(-\dfrac{\sqrt{2}}{2}-i\dfrac{\sqrt{2}}{2}\right)\\ &= -4\dfrac{\sqrt{2}}{2}-i\cdot 4\dfrac{\sqrt{2}}{2}\\&=-2\sqrt{2}-2\sqrt{2}\cdot i\end{aligned} \nonumber\]