1.3: Rates of Change and Behavior of Graphs
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Find the average rate of change of a function.
- Use a graph to determine where a function is increasing, decreasing, or constant.
- Use a graph to locate local maxima and local minima.
- Use a graph to locate the absolute maximum and absolute minimum.
Gasoline costs have experienced some wild fluctuations over the last several decades. Table
| 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |
| 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
If we were interested only in how the gasoline prices changed between 2005 and 2012, we could compute that the cost per gallon had increased from $2.31 to $3.68, an increase of $1.37. While this is interesting, it might be more useful to look at how much the price changed per year. In this section, we will investigate changes such as these.
Finding the Average Rate of Change of a Function
The price change per year is a rate of change because it describes how an output quantity changes relative to the change in the input quantity. We can see that the price of gasoline in Table
The Greek letter
In our example, the gasoline price increased by $1.37 from 2005 to 2012. Over 7 years, the average rate of change was
On average, the price of gas increased by about 19.6¢ each year. Other examples of rates of change include:
- A population of rats increasing by 40 rats per week
- A car traveling 68 miles per hour (distance traveled changes by 68 miles each hour as time passes)
- A car driving 27 miles per gallon (distance traveled changes by 27 miles for each gallon)
- The current through an electrical circuit increasing by 0.125 amperes for every volt of increased voltage
- The amount of money in a college account decreasing by $4,000 per quarter
Definition: Rate of Change
A rate of change describes how an output quantity changes relative to the change in the input quantity. The units on a rate of change are “output units per input units.”
The average rate of change between two input values is the total change of the function values (output values) divided by the change in the input values.
How To...
Given the value of a function at different points, calculate the average rate of change of a function for the interval between two values
- Calculate the difference
- Calculate the difference
- Find the ratio
Example
Using the data in Table
Solution
In 2007, the price of gasoline was $2.84. In 2009, the cost was $2.41. The average rate of change is
Analysis
Note that a decrease is expressed by a negative change or “negative increase.” A rate of change is negative when the output decreases as the input increases or when the output increases as the input decreases.
Exercise
Using the data in Table
- Solution
-
Example
Given the function
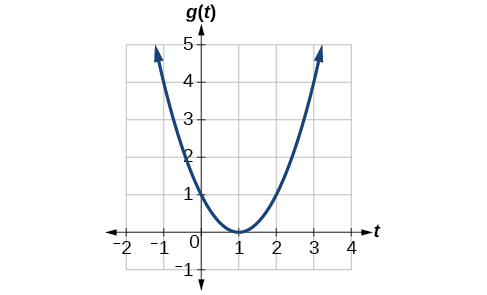
Solution
At
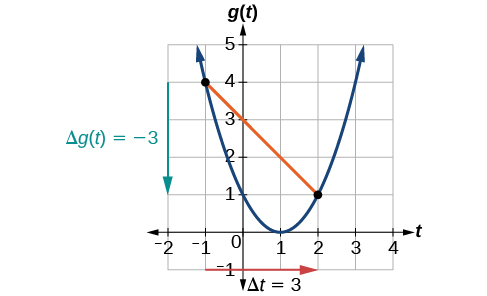
The horizontal change
Analysis
Note that the order we choose is very important. If, for example, we use
Example
After picking up a friend who lives 10 miles away, Anna records her distance from home over time. The values are shown in Table
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 10 | 55 | 90 | 153 | 214 | 240 | 292 | 300 |
Solution
Here, the average speed is the average rate of change. She traveled 292 miles in 6 hours, for an average speed of
The average speed is about 47 miles per hour.
Analysis
Because the speed is not constant, the average speed depends on the interval chosen. For the interval
Example
Compute the average rate of change of
Solution
We can start by computing the function values at each endpoint of the interval.
Now we compute the average rate of change.
Exercise
Find the average rate of change of
- Solution
-
Example
The electrostatic force
Solution
We are computing the average rate of change of
The average rate of change is
Example
Find the average rate of change of
Solution
We use the average rate of change formula.
Exercise
Find the average rate of change of
- Solution
-
Using a Graph to Determine Where a Function is Increasing, Decreasing, or Constant
As part of exploring how functions change, we can identify intervals over which the function is changing in specific ways. We say that a function is increasing on an interval if the function values increase as the input values increase within that interval. Similarly, a function is decreasing on an interval if the function values decrease as the input values increase over that interval. The average rate of change of an increasing function is positive, and the average rate of change of a decreasing function is negative. Figure
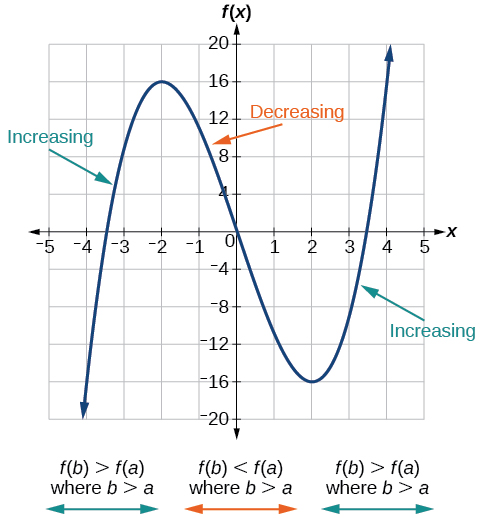
While some functions are increasing (or decreasing) over their entire domain, many others are not. A value of the input where a function changes from increasing to decreasing (as we go from left to right, that is, as the input variable increases) is called a local maximum. If a function has more than one, we say it has local maxima. Similarly, a value of the input where a function changes from decreasing to increasing as the input variable increases is called a local minimum. The plural form is “local minima.” Together, local maxima and minima are called local extrema, or local extreme values, of the function. (The singular form is “extremum.”) Often, the term local is replaced by the term relative. In this text, we will use the term local.
Clearly, a function is neither increasing nor decreasing on an interval where it is constant. A function is also neither increasing nor decreasing at extrema. Note that we have to speak of local extrema, because any given local extremum as defined here is not necessarily the highest maximum or lowest minimum in the function’s entire domain.
For the function whose graph is shown in Figure
![Graph of a polynomial that shows the increasing and decreasing intervals and local maximum.] Definition of a local maximum](https://math.libretexts.org/@api/deki/files/916/CNX_Precalc_Figure_01_03_014.jpg?revision=1)
To locate the local maxima and minima from a graph, we need to observe the graph to determine where the graph attains its highest and lowest points, respectively, within an open interval. Like the summit of a roller coaster, the graph of a function is higher at a local maximum than at nearby points on both sides. The graph will also be lower at a local minimum than at neighboring points. Figure
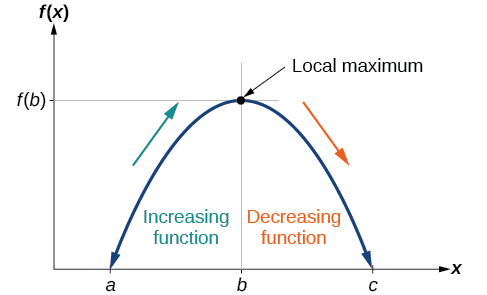
These observations lead us to a formal definition of local extrema.
Local Minima and Local Maxima
- A function
- A function
A function
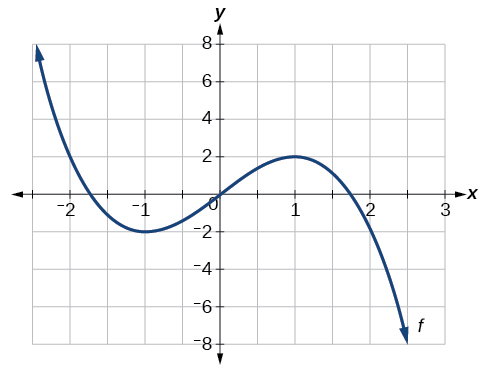
Example
Given the function
![[Graph of a polynomial.]](https://math.libretexts.org/@api/deki/files/920/CNX_Precalc_Figure_01_03_006.jpg?revision=1)
Solution
We see that the function is not constant on any interval. The function is increasing where it slants upward as we move to the right and decreasing where it slants downward as we move to the right. The function appears to be increasing from
In interval notation, we would say the function appears to be increasing on the interval
Analysis
Notice in this example that we used open intervals (intervals that do not include the endpoints), because the function is neither increasing nor decreasing at
Example
Graph the function
Solution
Using technology, we find that the graph of the function looks like that in Figure
 .
.
Analysis
Most graphing calculators and graphing utilities can estimate the location of maxima and minima. Figure
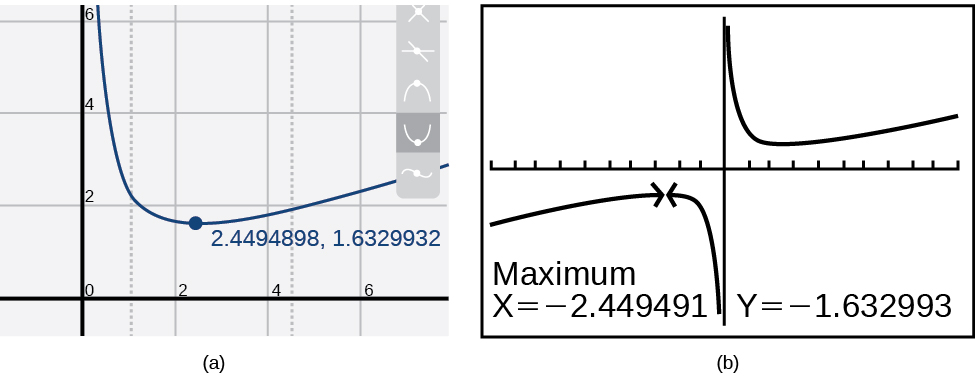
Based on these estimates, the function is increasing on the interval
Exercise
Graph the function
- Solution
-
The local maximum appears to occur at
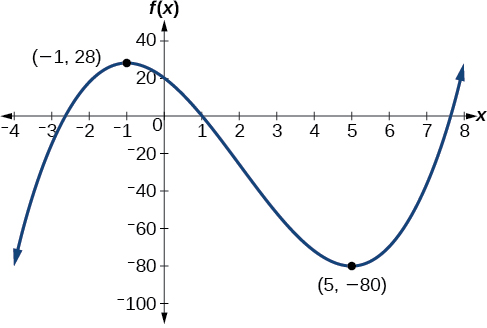
Graph of a polynomial with a local maximum at (-1, 28) and local minimum at (5, -80).
Example
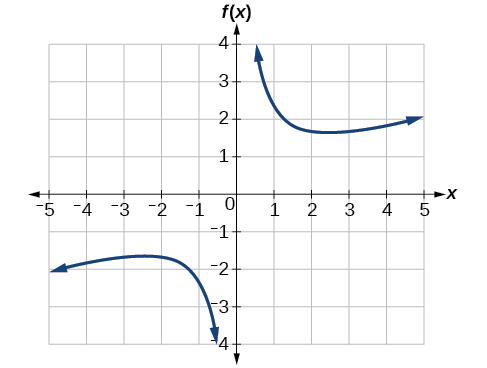
For the function f whose graph is shown in Figure
Solution
Observe the graph of
The graph attains a local minimum at
Analyzing the Toolkit Functions for Increasing or Decreasing Intervals
We will now return to our toolkit functions and discuss their graphical behavior in Figure
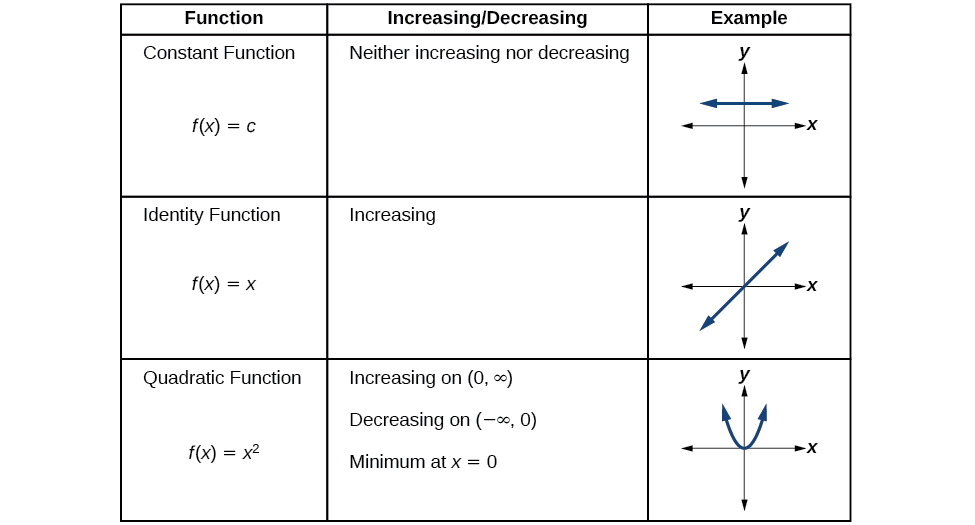
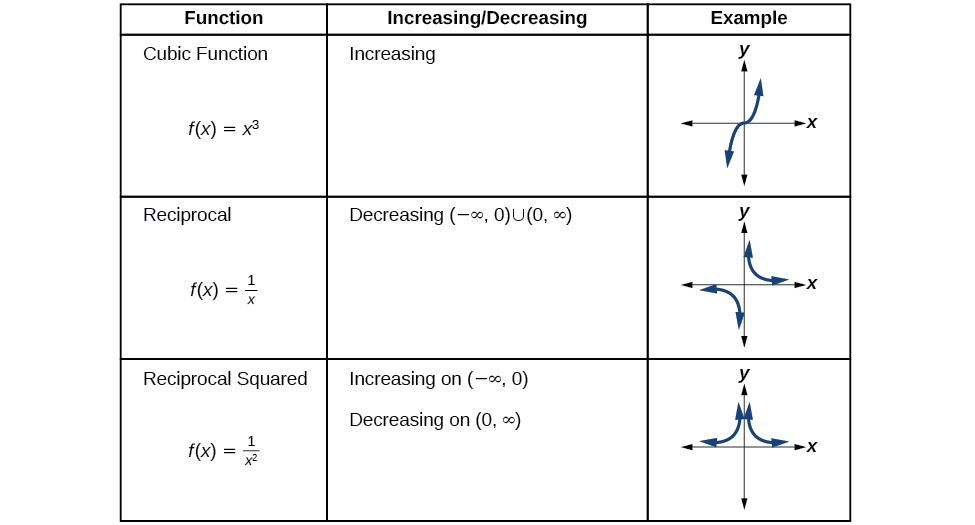 .
.
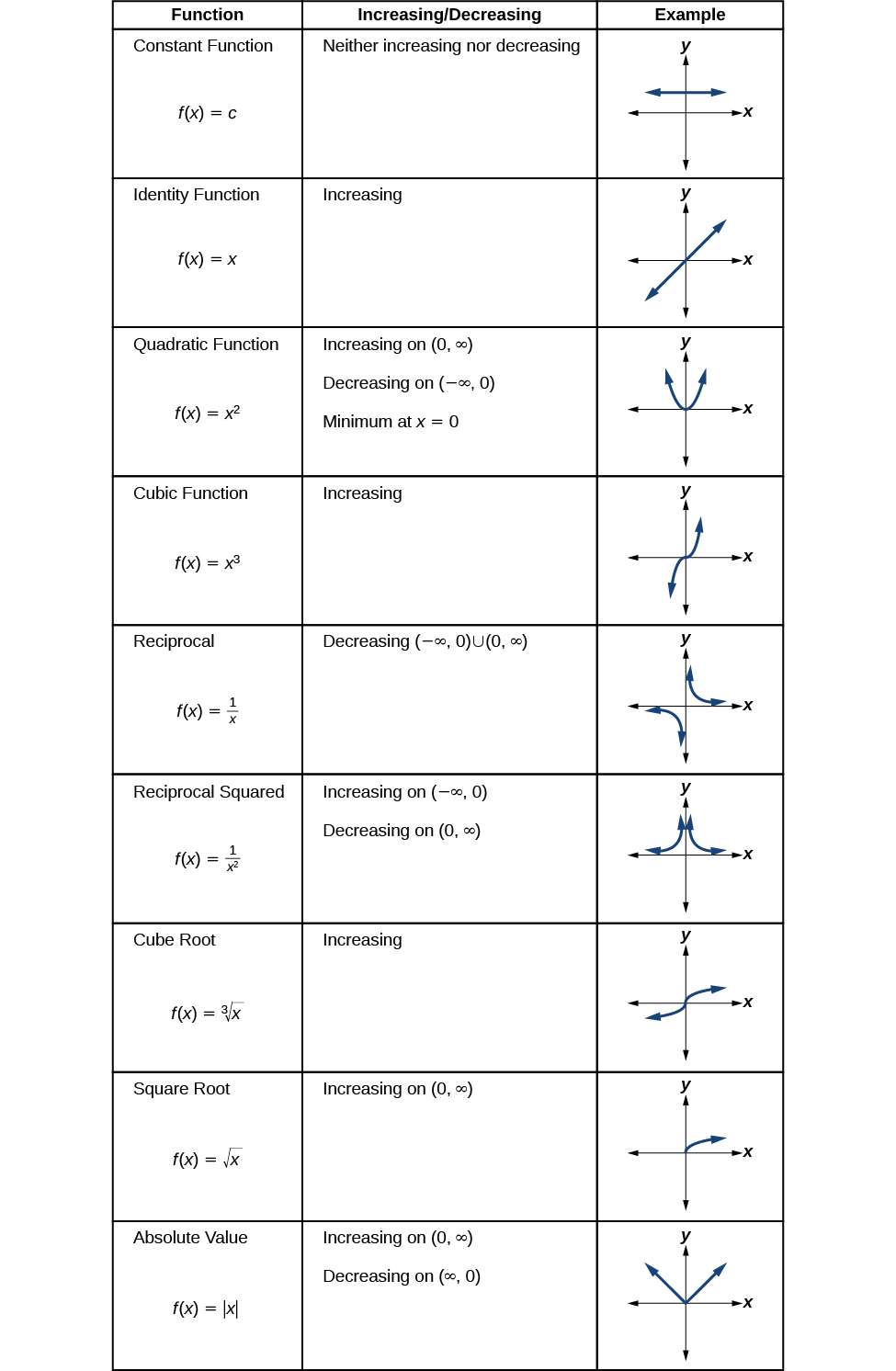
Figure
Use A Graph to Locate the Absolute Maximum and Absolute Minimum
There is a difference between locating the highest and lowest points on a graph in a region around an open interval (locally) and locating the highest and lowest points on the graph for the entire domain. The y-coordinates (output) at the highest and lowest points are called the absolute maximum and absolute minimum, respectively. To locate absolute maxima and minima from a graph, we need to observe the graph to determine where the graph attains it highest and lowest points on the domain of the function (Figure
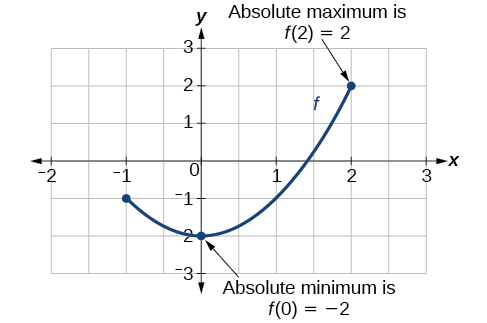
Not every function has an absolute maximum or minimum value. The toolkit function
Absolute Maxima and Minima
- The absolute maximum of
- The absolute minimum of
Example
For the function f shown in Figure
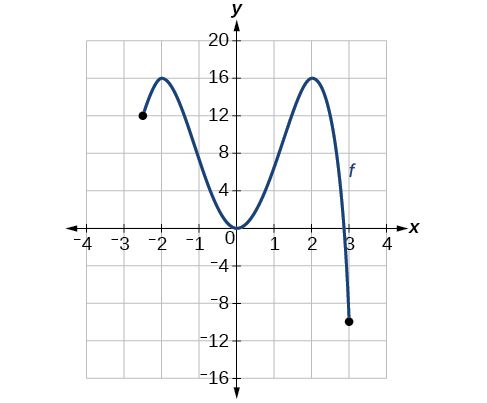
Solution
Observe the graph of
The graph attains an absolute minimum at x=3, because it is the lowest point on the domain of the function’s graph. The absolute minimum is the y-coordinate at x=3,which is−10.
Key Equations
- Average rate of change:
Key Concepts
- A rate of change relates a change in an output quantity to a change in an input quantity. The average rate of change is determined using only the beginning and ending data. See Example.
- Identifying points that mark the interval on a graph can be used to find the average rate of change. See Example.
- Comparing pairs of input and output values in a table can also be used to find the average rate of change. See Example.
- An average rate of change can also be computed by determining the function values at the endpoints of an interval described by a formula. See Example and Example.
- The average rate of change can sometimes be determined as an expression. See Example.
- A function is increasing where its rate of change is positive and decreasing where its rate of change is negative. See Example.
- A local maximum is where a function changes from increasing to decreasing and has an output value larger (more positive or less negative) than output values at neighboring input values.
- A local minimum is where the function changes from decreasing to increasing (as the input increases) and has an output value smaller (more negative or less positive) than output values at neighboring input values.
- Minima and maxima are also called extrema.
- We can find local extrema from a graph. See Example and Example.
- The highest and lowest points on a graph indicate the maxima and minima. See Example.


