6.E: Periodic Functions (Exercises)
- Page ID
- 17850
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.1: Graphs of the Sine and Cosine Functions
In the chapter on Trigonometric Functions, we examined trigonometric functions such as the sine function. In this section, we will interpret and create graphs of sine and cosine functions
Verbal
1) Why are the sine and cosine functions called periodic functions?
- Answer
-
The sine and cosine functions have the property that \(f(x+P)=f(x)\) for a certain \(P\). This means that the function values repeat for every \(P\) units on the \(x\)-axis.
2) How does the graph of \(y=\sin x\) compare with the graph of \(y=\cos x\)? Explain how you could horizontally translate the graph of \(y=\sin x\) to obtain \(y=\cos x\).
3) For the equation \(A \cos(Bx+C)+D\)
- Answer
-
The absolute value of the constant \(A\) (amplitude) increases the total range and the constant \(D\) (vertical shift) shifts the graph vertically.
4) How does the range of a translated sine function relate to the equation \(y=A \sin(Bx+C)+D\)
5) How can the unit circle be used to construct the graph of \(f(t)=\sin t\)?
- Answer
-
At the point where the terminal side of \(t\) intersects the unit circle, you can determine that the \(\sin t\) equals the \(y\)-coordinate of the point.
Graphical
For the following exercises, graph two full periods of each function and state the amplitude, period, and midline. State the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period for \(x>0\). Round answers to two decimal places if necessary.
6) \(f(x)=2\sin x\)
7) \(f(x)=\dfrac{2}{3}\cos x\)
- Answer
-
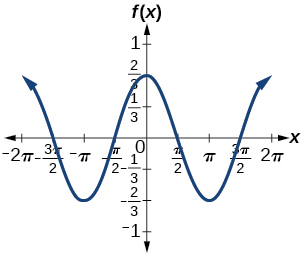
amplitude: \(\dfrac{2}{3}\)
; ; ; ; ;
8) \(f(x)=-3\sin x\)
9) \(f(x)=4\sin x\)
- Answer
-
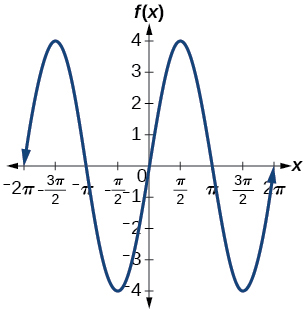
amplitude: \(4\); period: \(2\pi \)
; ; ; ;
10) \(f(x)=2\cos x\)
11) \(f(x)=\cos (2x)\)
- Answer
-
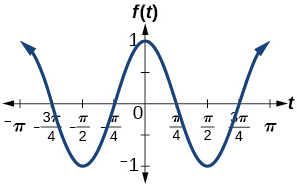
amplitude: \(1\); period: \(\pi\)
; ; ; ;
12) \(f(x)=2 \sin \left(\dfrac{1}{2}x\right)\)
13) \(f(x)=4 \cos(\pi x)\)
- Answer
-
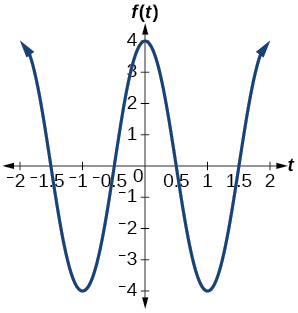
amplitude: \(4\); period: \(2\); midline: \(y=0\)
; ;
14) \(f(x)=3 \cos\left(\dfrac{6}{5}x\right)\)
15) \(y=3 \sin(8(x+4))+5\)
- Answer
-
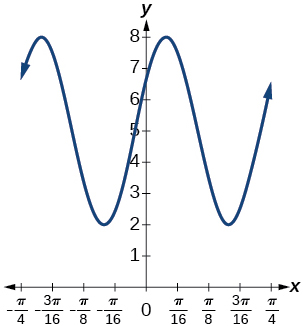
amplitude: \(3\); period: \(\dfrac{\pi}{4}\); midline: \(y=5\);
maximum: \(y=8\) occurs at \(x = -4+\frac{21\pi}{16} \approx 0.123\);
minimum: \(y=2\) occurs at \(x = -4+\frac{23\pi}{16} \approx 0.516\);
horizontal shift: \(-4\); vertical translation \(5\);
one period occurs from \(x=-4+\frac{22\pi}{16} \approx 0.320\) to \(x=-4+\frac{26\pi}{16} \approx 1.105 \)
16) \(y=2 \sin(3x-21)+4\)
17) \(y=5 \sin(5x+20)-2\)
- Answer
-
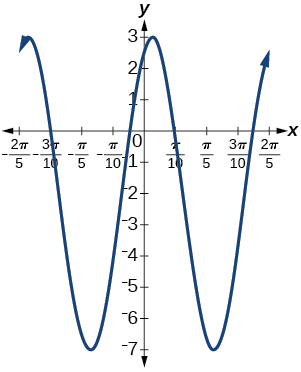
amplitude: \(5\); period:\(\dfrac{2\pi }{5}\); midline: \(y=-2\);
maximum: \(y=3\) occurs at \(x= -4+\frac{13\pi}{10} \approx 0.084\);
minimum: \(y=-7\) occurs at \(x=-4+\frac{15\pi}{10} \approx 0.712\);
phase shift: \(-4\); vertical translation: \(-2\);
one full period can be graphed on \(x=-4+\frac{7\pi}{5} \approx 0.398\) to\(x=-4+\frac{9\pi}{5} \approx 1.655 \)
For the following exercises, graph one full period of each function, starting at \(x=0\).
For each function, state the amplitude, period, and midline.
State the maximum and minimum \(y\)-values and their corresponding \(x\)-values on one period for \(x>0\).
State the phase shift and vertical translation, if applicable.
Round answers to two decimal places if necessary.
18) \(f(t)=2\sin \left(t-\dfrac{5\pi}{6} \right)\)
19) \(f(t)=-\cos \left(t+\dfrac{\pi}{3} \right)+1\)
- Answer
-
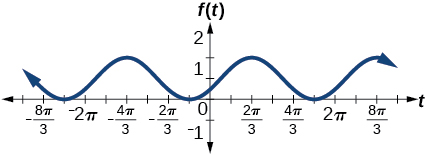
amplitude: \(1\); period: \(2\pi \); midline: \(y=1\);
maximum: \(y=2\) occurs at \(t=\frac{2\pi}{3} \approx 2.094\);
minimum: \(y=0\) occurs at \(t=\frac{2\pi}{3} \approx5.24\);
phase shift: \(-\dfrac{\pi}{3}\); vertical translation: \(1\);
one full period is from \(t=\frac{2\pi}{3} \approx 2.094\) to \(t=\frac{8\pi}{3} \approx 8.378 \)
20) \(f(t)=4\cos \left(2\left (t+\dfrac{\pi}{4} \right ) \right)-3\)
21) \(f(t)=-\sin \left (\dfrac{1}{2}t+\dfrac{5\pi}{3} \right )\)
- Answer
-
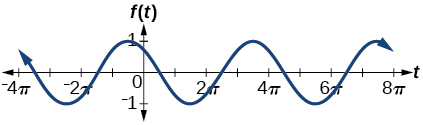 amplitude: \(1\); period: \(4\pi\); midline: \(y=0\);
amplitude: \(1\); period: \(4\pi\); midline: \(y=0\);
maximum: \(y=1\) occurs at \(t=\frac{11\pi}{3} \approx 11.52\);
minimum: \(y=-1\) occurs at \(t=\frac{5\pi}{3} \approx 5.24\);
phase shift: \(-\dfrac{10\pi}{3}\); vertical shift: \(0\);
one full period is from \(t=\frac{2\pi}{3} \approx 2.094\) to \(t=\frac{14\pi}{3} \approx 14.661 \)
22) \(f(x)=4\sin \left (\dfrac{\pi}{2}(x-3) \right )+7\)
23) Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in Figure below.
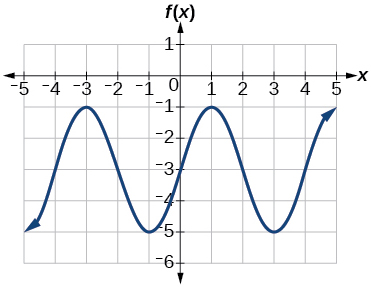
- Answer
-
23. amplitude: \(2\); midline: \(y=-3\) period: \(4\); equation: \(f(x)=2\sin \left (\dfrac{\pi}{2}x \right )-3\)
24) Determine the amplitude, midline, period, and an equation involving the cosine function for the graph shown in Figure below.
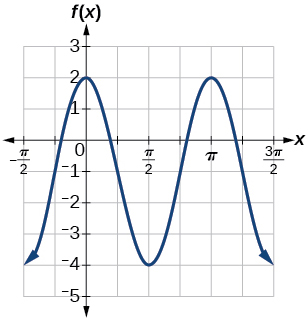
25) Determine the amplitude, midline, period, and an equation involving the cosine function for the graph shown in Figure below.
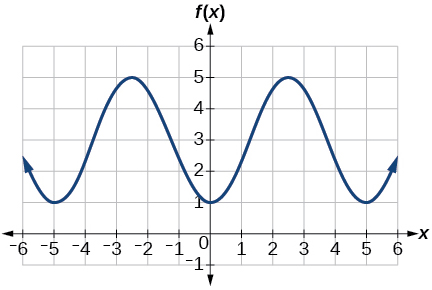
- Answer
-
25. amplitude: \(2\); period: \(5\); midline: \(y=3\) equation: \(f(x)=-2\cos \left (\dfrac{2\pi}{5}x \right )+3\)
26) Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in Figure below.
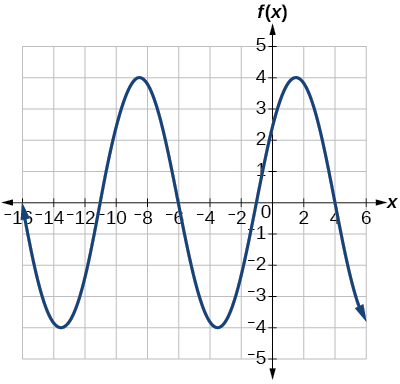
27) Determine the amplitude, midline, period, and an equation involving the cosine function for the graph shown in Figure below.
- Answer
-
27. amplitude: \(4\); period: \(2\); midline: \(y=0\) ; equation: \(f(x)=-4\cos \left (\pi \left (x-\dfrac{\pi}{2} \right ) \right )\)
28) Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in Figure below.
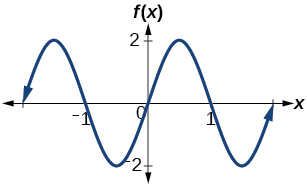
29) Determine the amplitude, midline, period, and an equation involving the cosine function for the graph shown in Figure below.
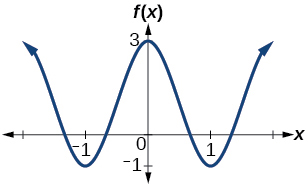
- Answer
-
29. amplitude: \(2\); period: \(2\); midline \(y=1\) equation: \(f(x)=2\cos \left (\pi x \right )+1\)
30) Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in Figure below.
Algebraic
For the following exercises, let \(f(x)=\sin x \)
31) On \([0,2\pi )\)
32) On \([0,2\pi )\), solve \(f(x)=\dfrac{1}{2}\).
- Answer
-
\(\dfrac{\pi }{6}\), \(\dfrac{5\pi }{6}\)
33) Evaluate \(f \left( \dfrac{\pi }{2} \right) \)
34) On \([0,2\pi)\), \(f(x)=\dfrac{\sqrt{2}}{2}\). Find all values of \(x\).
- Answer
-
\(\dfrac{\pi }{4}\), \(\dfrac{3\pi }{4}\)
35) On \([0,2\pi )\)
36) On \([0,2\pi )\)
- Answer
-
\(\dfrac{3\pi }{2}\)
37) Show that \(f(-x) = -f(x)\)
For the following exercises, let \(f(x)=\cos x\)
38) On \([0,2\pi )\)
- Answer
-
\(\dfrac{\pi }{2}\), \(\dfrac{3\pi }{2}\)
39) On \([0,2\pi )\)
40) On \([0,2\pi )\)
- Answer
-
\(\dfrac{\pi }{2}\), \(\dfrac{3\pi }{2}\)
41) On \([0,2\pi )\)
42) On \([0,2\pi )\)
- Answer
-
\(\dfrac{\pi }{6}\), \(\dfrac{11\pi }{6}\)
Technology
43) Graph \(h(x)=x+\sin x\) on \([0,2\pi ]\)
44) Graph \(h(x)=x+\sin x\) on \([-100,100]\)
- Answer
-
The graph appears linear. The linear functions dominate the shape of the graph for large values of \(x\).
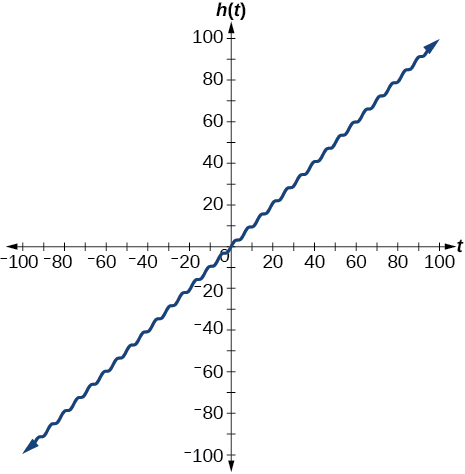
45) Graph \(f(x)=x\sin x\) on \([0,2\pi ]\) and verbalize how the graph varies from the graph of \(f(x)=x\sin x\).
46) Graph \(f(x)=x\sin x\) on the window \([-10,10]\) and explain what the graph shows.
- Answer
-
The graph is symmetric with respect to the \(y\)-axis and there is no amplitude because the function is not periodic.
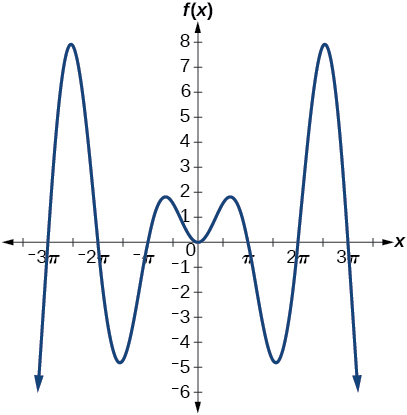
47) Graph \(f(x)=\dfrac{\sin x}{x}\) on the window \([-5\pi , 5\pi ]\) and explain what the graph shows.
Real-World Applications
48) A Ferris wheel is \(25\) meters in diameter and boarded from a platform that is \(1\) meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes \(1\) full revolution in \(10\) minutes. The function \(h(t)\) gives a person’s height in meters above the ground \(t\) minutes after the wheel begins to turn
- Find the amplitude, midline, and period of \(h(t)\).
- Find a formula for the height function \(h(t)\).
- How high off the ground is a person after \(5\) minutes?
- Answer
-
- Amplitude: \(12.5\); period: \(10\); midline: \(y=13.5\)
- \(h(t)=12.5\sin\left ( \dfrac{\pi}{5}(t-2.5) \right )+13.5\)
- \(26\) ft
6.2: Graphs of the Other Trigonometric Functions
This section addresses the graphing of the Tangent, Cosecant, Secant, and Cotangent curves.
Verbal
1) Explain how the graph of the sine function can be used to graph \(y=\csc x\).
Answer
Since \(y=\csc x\) is the reciprocal function of \(y=\sin x\)
2) How can the graph of \(y=\cos x\) be used to construct the graph of \(y=\sec x\)?
3) Explain why the period of \(y=\tan x\) is equal to \(\pi \).
Answer
Answers will vary. Using the unit circle, one can show that \(y=\tan (x+\pi )=\tan x\).
4) Why are there no intercepts on the graph of \(y=\csc x\)?
5) How does the period of \(y=\csc x\) compare with the period of \(y=\sin x\)?
Answer
-
The period is the same: \(2\pi \)
Algebraic
For the exercises 6-9, match each trigonometric function with one of the following graphs.
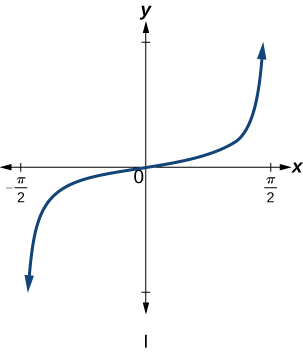
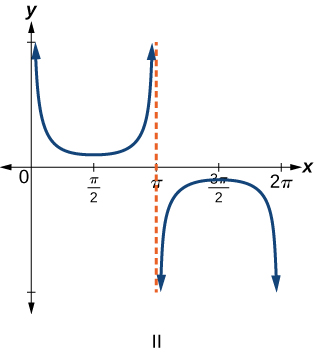
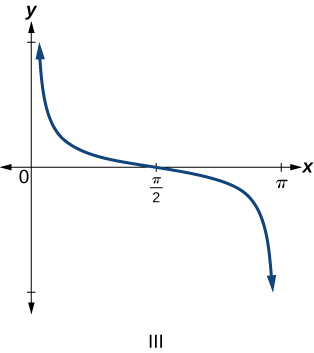
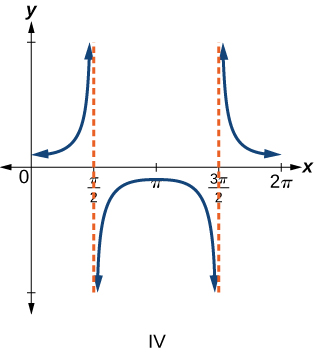
6) \(f(x)=\tan x\)
7) \(f(x)=\sec x\)
- Answer
-
\(\mathrm{IV}\)
8) \(f(x)=\csc x\)
9) \(f(x)=\cot x\)
- Answer
-
\(\mathrm{III}\)
For the exercises 10-16, find the period and horizontal shift of each of the functions.
10) \(f(x)=2\tan(4x-32)\)
11) \(h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)\)
- Answer
-
period: \(8\); horizontal shift: \(1\) unit to left
12) \(m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)\)
13) If \(\tan x=-1.5\)
- Answer
-
\(1.5\)
14) If \(\sec x=2\), find \(\sec (-x)\).
15) If \(\csc x=-5\), find \(\csc (-x)\).
- Answer
-
\(5\)
16) If \(x\sin x=2\), find \((-x)\sin (-x)\).
For the exercises 17-18, rewrite each expression such that the argument \(x\) is positive.
17) \(\cot(-x)\cos(-x)+\sin(-x)\)
- Answer
-
\(-\cot x \cos x-\sin x\)
18) \(\cos(-x)+\tan(-x)\sin(-x)\)
Graphical
For the exercises 19-36, sketch two periods of the graph for each of the following functions. Identify the stretching factor, period, and asymptotes.
19) \(f(x)=2\tan(4x-32)\)
- Answer
-
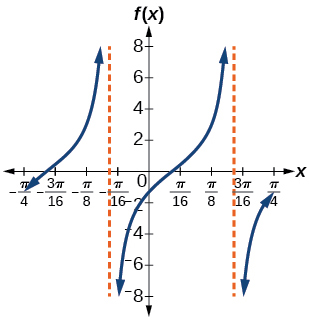
stretching factor: \(2\); period: \(\dfrac{\pi }{3}\)
;
20) \(h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)\)
21) \(m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)\)
- Answer
-
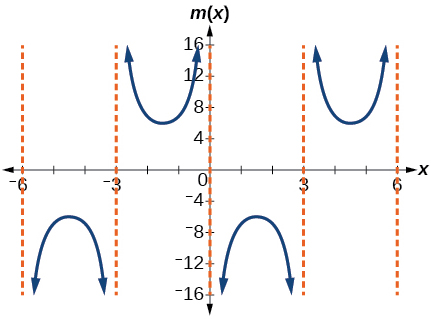
stretching factor: \(6\); period: \(6\); asymptotes: \(x=k\), where \(k\) is an integer
22) \(j(x)=\tan \left ( \dfrac{\pi }{2}x \right )\)
23) \(p(x)=\tan \left ( x-\dfrac{\pi }{2} \right )\)
- Answer
-
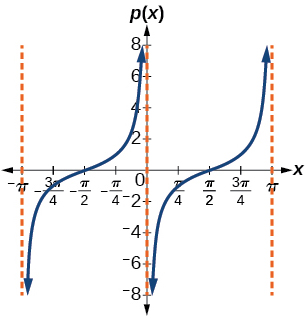
stretching factor: \(1\); period: \(\pi \)
;
24) \(f(x)=4\tan (x)\)
25) \(f(x)=\tan \left ( x+\dfrac{\pi }{4} \right )\)
- Answer
-
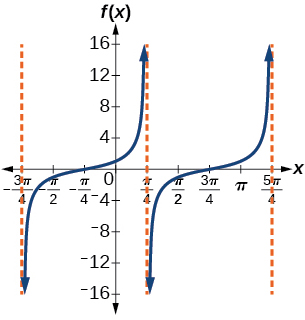
Stretching factor: \(1\); period: \(\pi \)
;
26) \(f(x)=\pi \tan(\pi x- \pi)-\pi\)
27) \(f(x)=2\csc (x)\)
- Answer
-
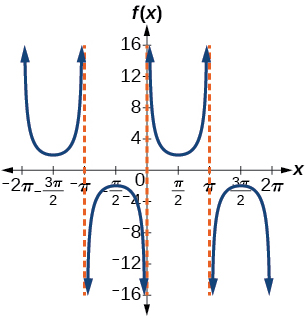
stretching factor: \(2\); period: \(2\pi \)
;
28) \(f(x)=-\dfrac{1}{4}\csc(x)\)
29) \(f(x)=4\sec(3x)\)
- Answer
-
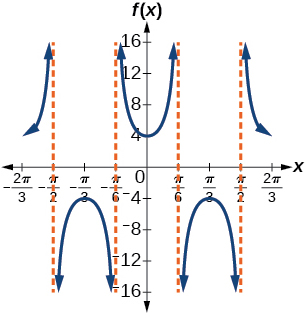
stretching factor: \(4\); period: \(\dfrac{2\pi }{3}\)
;
30) \(f(x)=-3\cot(2x)\)
31) \(f(x)=7\sec(5x)\)
- Answer
-
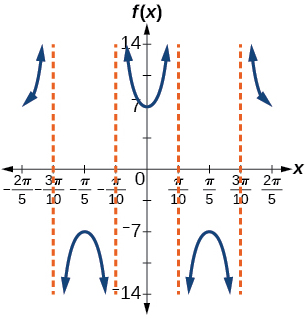
stretching factor: \(7\); period: \(\dfrac{2\pi }{5}\)
;
32) \(f(x)=\dfrac{9}{10}\csc(\pi x)\)
33) \(f(x)=2\csc \left(x+\dfrac{\pi }{4} \right)-1\)
- Answer
-
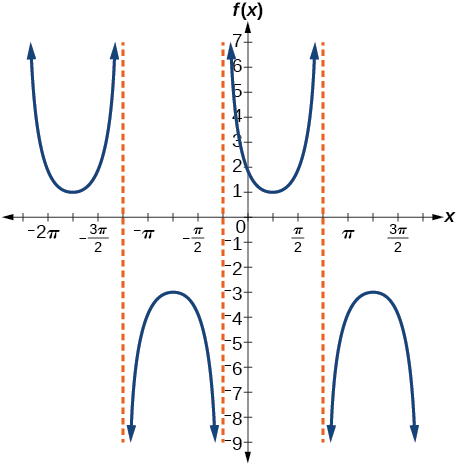
Stretching factor: \(2\); period: \(2\pi \) ; asymptotes: \(x=-\dfrac{\pi}{4}+\pi k\), where \(k\) is an integer
34) \(f(x)=-\sec \left(x-\dfrac{\pi }{3} \right)-2\)
35) \(f(x)=\dfrac{7}{5}\csc \left(x-\dfrac{\pi }{4} \right)\)
- Answer
-
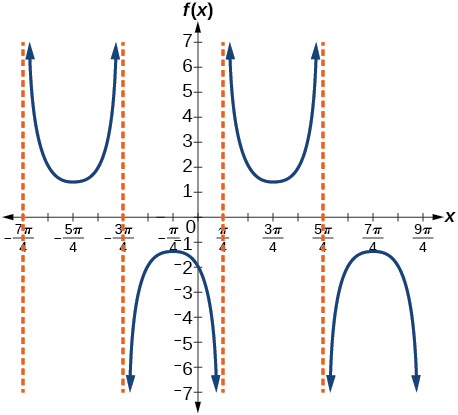
Stretching factor: \(\dfrac{7}{5}\); period: \(2\pi \) ; asymptotes: \(x=\dfrac{\pi}{4}+\pi k\), where \(k\) is an integer
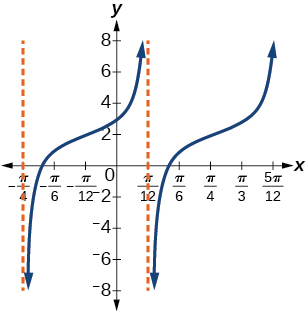
36) \(f(x)=5\left (\cot \left(x+\dfrac{\pi }{2} \right) -3 \right )\)
37) A tangent curve, \(A=1\)
- Answer
-
\(y=\tan\left(3\left(x-\dfrac{\pi}{4} \right) \right)+2\)
38) A tangent curve, \(A=-2\), period of \(\dfrac{\pi }{4}\); and phase shift \((h, k)=\left (- \dfrac{\pi }{4},-2 \right )\)
For the exercises 39-45, find an equation for the graph of each function.
39)
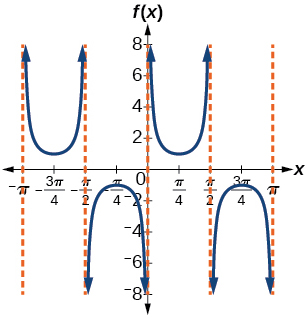
- Answer
-
\(f(x)=\csc (2x)\)
40)
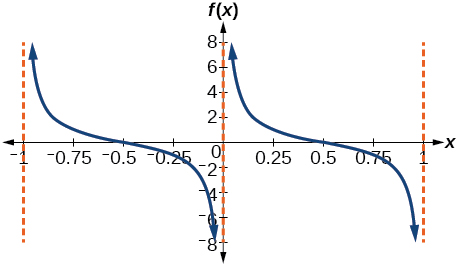
41)
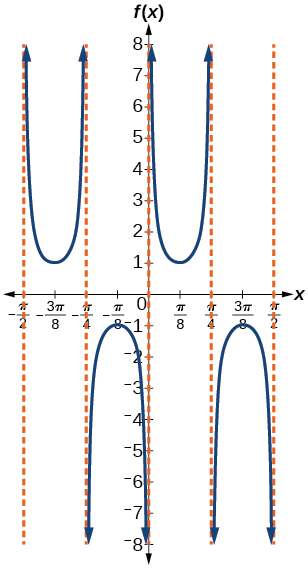
- Answer
-
\(f(x)=\csc (4x)\)
42)
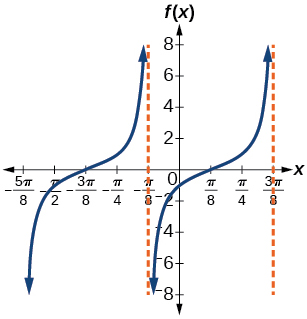
43)
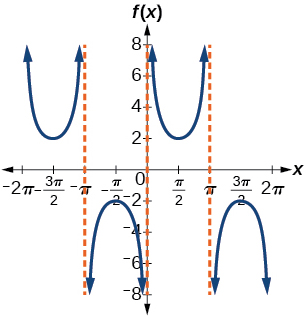
- Answer
-
\(f(x)=2\csc x\)
44)
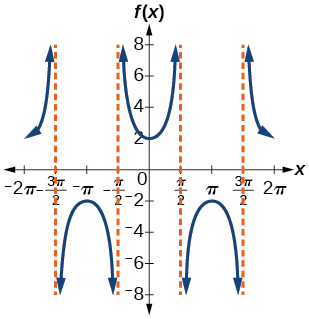
45)
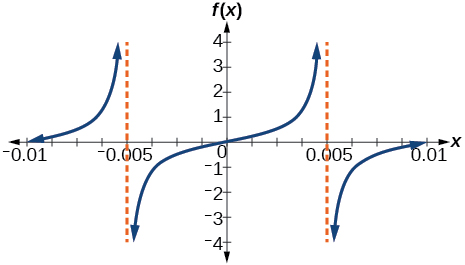
- Answer
-
\(f(x)=\dfrac{1}{2}\tan (100\pi x)\)
Technology
For the exercises 46-53, use a graphing calculator to graph two periods of the given function. Note: most graphing calculators do not have a cosecant button; therefore, you will need to input \(\csc x\) as \(\dfrac{1}{\sin x}\)
46) \(f(x)=| \csc (x) |\)
47) \(f(x)=| \cot (x) |\)
- Answer
-
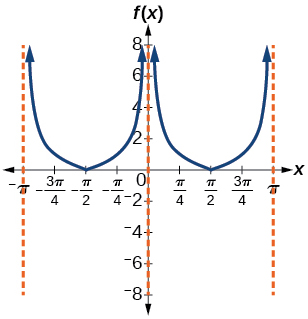
48) \(f(x)=2^{\csc (x)}\)
49) \(f(x)=\frac{\csc (x)}{\sec (x)}\)
- Answer
-
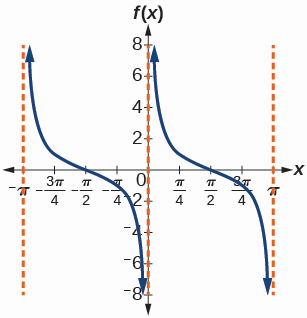
50) Graph \(f(x)=1+\sec^2(x)-\tan^2(x)\)
51) \(f(x)=\sec(0.001x)\)
- Answer
-
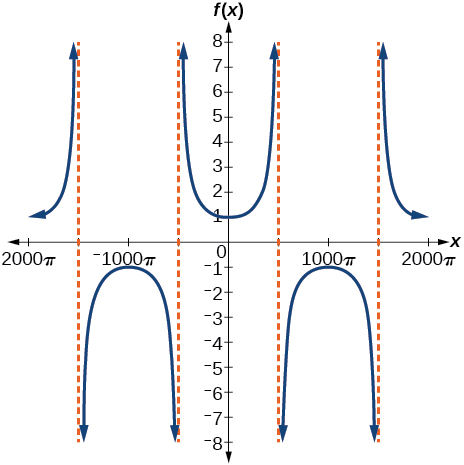
52) \(f(x)=\cot(100 \pi x)\)
53) \(f(x)=\sin^2x +\cos^2x\)
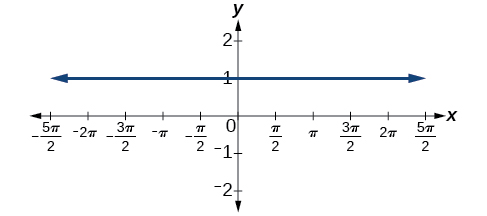
- Answer
-
Real-World Applications
54) The function \(f(x)=20\tan\left(\dfrac{\pi }{10}x\right)\) marks the distance in the movement of a light beam from a police car across a wall for time \(x\)
- Graph on the interval \([0,5]\)
- Find and interpret the stretching factor, period, and asymptote.
- Evaluate \(f(10)\) and \(f(2.5)\) and discuss the function’s values at those inputs.
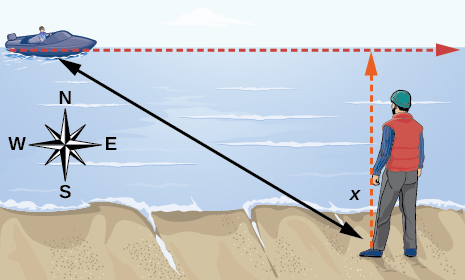
55) Standing on the shore of a lake, a fisherman sights a boat far in the distance to his left. Let \(x\)
- What is a reasonable domain for \(d(x)\)?
- Graph \(d(x)\) on this domain.
- Find and discuss the meaning of any vertical asymptotes on the graph of \(d(x)\).
- Calculate and interpret \(d\left ( -\dfrac{\pi }{3} \right )\)
. - Calculate and interpret \(d\left ( \dfrac{\pi }{6} \right )\)
. - What is the minimum distance between the fisherman and the boat? When does this occur?
- Answer
-
- \(\left ( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right )\)
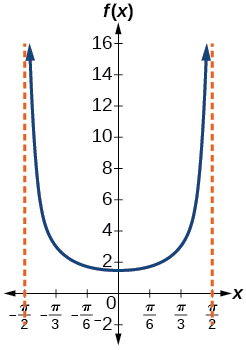
- \(x=-\dfrac{\pi }{2}\) and \(x=\dfrac{\pi }{2}\)
; - \(3\); when \(x=-\dfrac{\pi }{3}\)
, - \(1.73\); when \(x=\dfrac{\pi }{6}\)
, - \(1.5\) km; when \(x=0\)
56) A laser rangefinder is locked on a comet approaching Earth. The distance \(g(x)\)
- Graph \(g(x)\) on the interval \([0,35]\).
- Evaluate \(g(5)\) and interpret the information.
- What is the minimum distance between the comet and Earth? When does this occur? To which constant in the equation does this correspond?
- Find and discuss the meaning of any vertical asymptotes.
57) A video camera is focused on a rocket on a launching pad \(2\) miles from the camera. The angle of elevation from the ground to the rocket after \(x\) seconds is \(\dfrac{\pi }{120}x\).
- Write a function expressing the altitude \(h(x)\)
, - Graph \(h(x)\) on the interval \((0,60)\).
- Evaluate and interpret the values \(h(0)\) and \(h(30)\).
- What happens to the values of \(h(x)\) as \(x\) approaches \(60\) seconds? Interpret the meaning of this in terms of the problem.
- Answer
-
- \(h(x)=2\tan \left(\dfrac{\pi }{120}x \right)\)
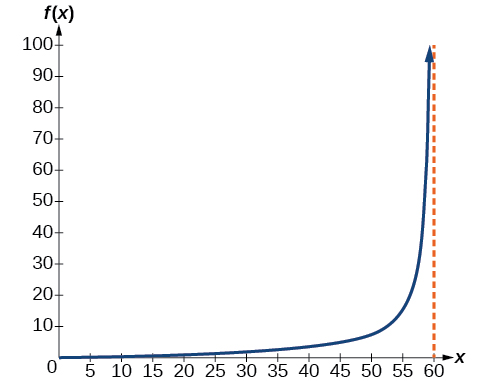
- \(h(0)=0\)
: : - As \(x\) approaches \(60\) seconds, the values of \(h(x)\) grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.
6.3: Inverse Trigonometric Functions
In this section, we will explore the inverse trigonometric functions. Inverse trigonometric functions “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa.
Verbal
1) Why do the functions \(f(x)=\sin^{-1}x\) and \(g(x)=\cos^{-1}x\) have different ranges?
- Answer
-
The function \(y=\sin x\) is one-to-one on \(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]\)
; ;
2) Since the functions \(y=\cos x\) and \(y=\cos^{-1}x\) are inverse functions, why is \(\cos^{-1}\left (\cos \left (-\dfrac{\pi }{6} \right ) \right )\)
3) Explain the meaning of \(\dfrac{\pi }{6}=\arcsin (0.5)\).
- Answer
-
\(\dfrac{\pi }{6}\) is the radian measure of an angle between \(-\dfrac{\pi }{2}\) and \(\dfrac{\pi }{2}\) whose sine is \(0.5\).
4) Most calculators do not have a key to evaluate \(\sec ^{-1}(2)\)
5) Why must the domain of the sine function, \(\sin x\)
- Answer
-
In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way. Mathematicians have agreed to restrict the sine function to the interval \(\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]\) so that it is one-to-one and possesses an inverse.
6) Discuss why this statement is incorrect: \(\arccos(\cos x)=x\) for all \(x\).
7) Determine whether the following statement is true or false and explain your answer: \(\arccos(-x)=\pi - \arccos x\)
- Answer
-
True . The angle, \(\theta _1\) that equals \(\arccos(-x)\), \(x>0\), will be a second quadrant angle with reference angle, \(\theta _2\), where \(\theta _2\) equals \(\arccos x\), \(x>0\). Since \(\theta _2\) is the reference angle for \(\theta _1\), \(\theta _2=\pi - \theta _1\) and \(\arccos(-x)=\pi - \arccos x-\)
Algebraic
For the exercises 8-16, evaluate the expressions.
8) \(\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)\)
9) \(\sin^{-1}\left(-\dfrac{1}{2}\right)\)
- Answer
-
\(-\dfrac{\pi }{6}\)
10) \(\cos^{-1}\left(-\dfrac{1}{2}\right)\)
11) \(\cos^{-1}\left(-\dfrac{\sqrt{2}}{2}\right)\)
- Answer
-
\(\dfrac{3\pi }{4}\)
12) \(\tan^{-1}(1)\)
13) \(\tan^{-1}(-\sqrt{3})\)
- Answer
-
\(-\dfrac{\pi }{3}\)
14) \(\tan^{-1}(-1)\)
15) \(\tan^{-1}(\sqrt{3})\)
- Answer
-
\(\dfrac{\pi }{3}\)
16) \(\tan^{-1}\left(\dfrac{-1}{\sqrt{3}}\right)\)
For the exercises 17-21, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
17) \(\cos^{-1}(-0.4)\)
- Answer
-
\(1.98\)
18) \(\arcsin (0.23)\)
19) \(\arccos \left(\dfrac{3}{5}\right)\)
- Answer
-
\(0.93\)
20) \(\cos^{-1}(-0.8)\)
21) \(\tan^{-1}(6)\)
- Answer
-
\(1.41\)
For the exercises 22-23, find the angle \(\theta\) in the given right triangle. Round answers to the nearest hundredth.
22)
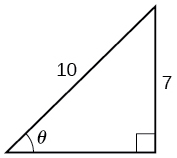
23)
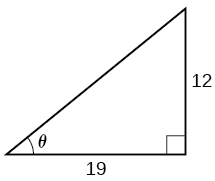
- Answer
-
\(0.56\) radians
For the exercises 24-36, find the exact value, if possible, without a calculator. If it is not possible, explain why.
24) \(\sin^{-1}(\cos(\pi))\)
25) \(\tan^{-1}(\sin(\pi))\)
- Answer
-
\(0\)
26) \(\cos^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)\)
27) \(\tan^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)\)
- Answer
-
\(0.71\)
28) \(\sin^{-1}\left(\cos \left(\dfrac{-\pi}{2} \right)\right)\)
29) \(\tan^{-1}\left(\sin \left(\dfrac{4\pi}{3} \right)\right)\)
- Answer
-
\(-0.71\)
30) \(\sin^{-1}\left(\sin \left(\dfrac{5\pi}{6} \right)\right)\)
31) \(\tan^{-1}\left(\sin \left(\dfrac{-5\pi}{2} \right)\right)\)
- Answer
-
\(-\dfrac{\pi}{4}\)
32) \(\cos \left(\sin^{-1} \left(\dfrac{4}{5} \right)\right)\)
33) \(\sin \left(\cos^{-1} \left(\dfrac{3}{5} \right)\right)\)
- Answer
-
\(0.8\)
34) \(\sin \left(\tan^{-1} \left(\dfrac{4}{3} \right)\right)\)
35) \(\cos \left(\tan^{-1} \left(\dfrac{12}{5} \right)\right)\)
- Answer
-
\(\dfrac{5}{13}\)
36) \(\cos \left(\sin^{-1} \left(\dfrac{1}{2} \right)\right)\)
For the exercises 37-41, find the exact value of the expression in terms of \(x\) with the help of a reference triangle.
37) \(\tan \left(\sin^{-1} (x-1)\right)\)
- Answer
-
\(\dfrac{x-1}{\sqrt{-x^2+2x}}\)
38) \(\sin \left(\sin^{-1} (1-x)\right)\)
39) \(\cos \left(\sin^{-1} \left(\dfrac{1}{x}\right)\right)\)
- Answer
-
\(\dfrac{\sqrt{x^2-1}}{x}\)
40) \(\cos \left(\tan^{-1} (3x-1)\right)\)
41) \(\tan \left(\sin^{-1} \left(x+\dfrac{1}{2}\right)\right)\)
- Answer
-
\(\dfrac{x+0.5}{\sqrt{-x^2-x+\tfrac{3}{4}}}\)
Extensions
For the exercise 42, evaluate the expression without using a calculator. Give the exact value.
2) \(\dfrac{\sin^{-1}\left ( \tfrac{1}{2} \right )-\cos^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\sin^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\cos^{-1}(1)}{\cos^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\sin^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\cos^{-1}\left ( \tfrac{1}{2} \right )-\sin^{-1}(0)}\)
For the exercises 43-47, find the function if \(\sin t = \dfrac{x}{x+1}\)
43) \(\cos t\)
- Answer
-
\(\dfrac{\sqrt{2x+1}}{x+1}\)
44) \(\sec t\)
45) \(\cot t\)
- Answer
-
\(\dfrac{\sqrt{2x+1}}{x}\)
46) \(\cos \left(\sin^{-1} \left(\dfrac{x}{x+1}\right)\right)\)
47) \(\tan^{-1} \left(\dfrac{x}{\sqrt{2x+1}}\right)\)
- Answer
-
\(t\)
Graphical
48) Graph \(y=\sin^{-1} x\) and state the domain and range of the function.
49) Graph \(y=\arccos x\)
- Answer
-
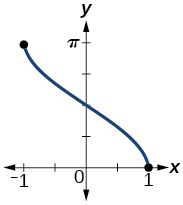
domain \([-1,1]\)
;
50) Graph one cycle of \(y=\tan^{-1} x\) and state the domain and range of the function.
51) For what value of \(x\) does \(\sin x=\sin^{-1} x\)? Use a graphing calculator to approximate the answer.
- Answer
-
approximately \(x=0.00\)
52) For what value of \(x\) does \(\cos x=\cos^{-1} x\)? Use a graphing calculator to approximate the answer.
Real-World Applications
53) Suppose a \(13\)-foot ladder is leaning against a building, reaching to the bottom of a second-floor window \(12\) feet above the ground. What angle, in radians, does the ladder make with the building?
Answer
-
\(0.395\) radians
54) Suppose you drive \(0.6\) miles on a road so that the vertical distance changes from \(0\) to \(150\) feet. What is the angle of elevation of the road?
55) An isosceles triangle has two congruent sides of length \(9\) inches. The remaining side has a length of \(8\) inches. Find the angle that a side of \(9\) inches makes with the \(8\)-inch side.
- Answer
-
\(1.11\) radians
56) Without using a calculator, approximate the value of \(\arctan (10,000)\)
57) A truss for the roof of a house is constructed from two identical right triangles. Each has a base of \(12\) feet and height of \(4\) feet. Find the measure of the acute angle adjacent to the \(4\)-foot side.
- Answer
-
\(1.25\) radians
58) The line \(y=\dfrac{3}{5}x\) passes through the origin in the \(x,y\)-plane. What is the measure of the angle that the line makes with the positive \(x\)-axis?
59) The line \(y=\dfrac{-3}{7}x\) passes through the origin in the \(x,y\)-plane. What is the measure of the angle that the line makes with the negative \(x\)-axis?
- Answer
-
\(0.405\) radians
60) What percentage grade should a road have if the angle of elevation of the road is \(4\) degrees? (The percentage grade is defined as the change in the altitude of the road over a \(100\)-foot horizontal distance. For example a \(5\%\) grade means that the road rises \(5\) feet for every \(100\) feet of horizontal distance.)
61) A \(20\)-foot ladder leans up against the side of a building so that the foot of the ladder is \(10\) feet from the base of the building. If specifications call for the ladder's angle of elevation to be between \(35\) and \(45\) degrees, does the placement of this ladder satisfy safety specifications?
- Answer
-
No. The angle the ladder makes with the horizontal is \(60\) degrees.
62) Suppose a \(15\)-foot ladder leans against the side of a house so that the angle of elevation of the ladder is \(42\) degrees. How far is the foot of the ladder from the side of the house?
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


