6.R: Periodic Functions (Review)
- Page ID
- 18275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.1: Graphs of the Sine and Cosine Functions
For the exercises 1-8, graph the functions for two periods and determine the amplitude or stretching factor, period, midline equation, and asymptotes.
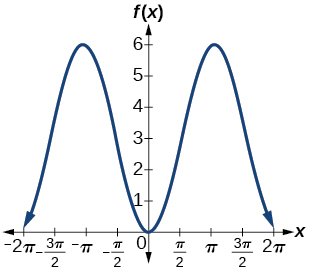
1) \(f(x)=-3\cos x+3\)
- Answer
-
amplitude: \(3\); period: \(2\pi \); midline: \(y=3\)
; 
2) \(f(x)=\dfrac{1}{4}\sin x\)
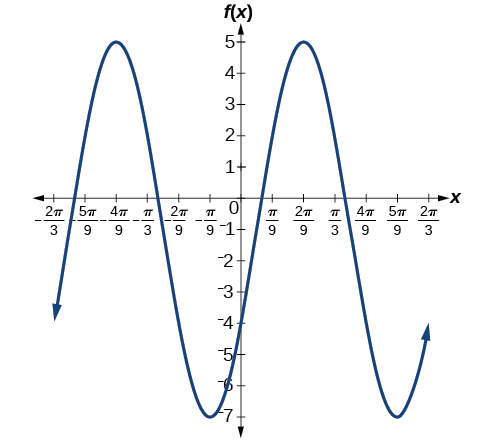
3) \(f(x)=3\cos\left ( x+\dfrac{\pi }{6} \right )\)
- Answer
-
amplitude: \(3\); period: \(2\pi \); midline: \(y=0\); no asymptotes
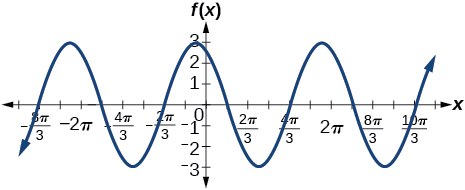
4) \(f(x)=-2\sin\left ( x-\dfrac{2\pi }{3} \right )\)
5) \(f(x)=3\sin\left ( x-\dfrac{\pi }{4} \right )-4\)
- Answer
-
amplitude: \(3\); period: \(2\pi \); midline: \(y=-4\); no asymptotes
6) \(f(x)=2\left (\cos\left ( x-\dfrac{4\pi }{3} \right )+1 \right )\)
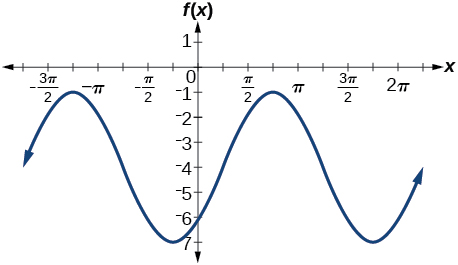
7) \(f(x)=6\sin\left ( 3x-\dfrac{\pi }{6} \right )-1\)
- Answer
-
amplitude: \(6\); period: \(dfrac{2\pi }{3}\); midline: \(y=-1\); no asymptotes
8) \(f(x)=-100\sin(50x-20)\)
6.2: Graphs of the Other Trigonometric Functions
For the exercises 1-4, graph the functions for two periods and determine the amplitude or stretching factor, period, midline equation, and asymptotes.
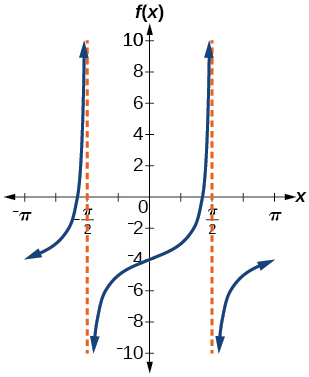
1) \(f(x)=\tan x-4\)
- Answer
-
stretching factor: none; period: \(\pi \)
; ; 
2) \(f(x)=2\tan \left ( x-\dfrac{\pi }{6} \right )\)
3) \(f(x)=-3\tan (4x)-2\)
- Answer
-
stretching factor: \(3\); period: \(\dfrac{\pi }{4}\); midline: \(y=-2\); asymptotes: \(x=\dfrac{\pi }{8}+\dfrac{\pi }{4}k\), where \(k\) is an integer
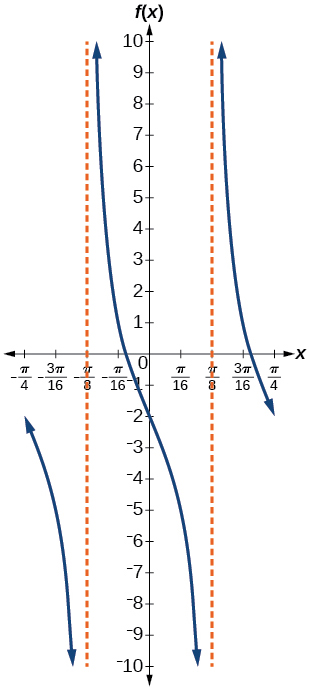
4) \(f(x)=0.2\cos(0.1x)+0.3\)
For the exercises 5-10, graph two full periods. Identify the period, the phase shift, the amplitude, and asymptotes.
5) \(f(x)=\dfrac{1}{3}\sec x\)
- Answer
-
amplitude: none; period: \(2\pi \); no phase shift; asymptotes: \(x=\dfrac{\pi }{2}k\), where \(k\) is an integer
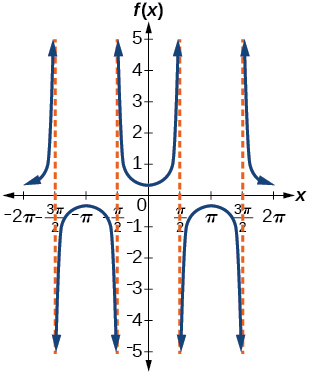
6) \(f(x)=3\cot x\)
7) \(f(x)=4\csc (5x)\)
- Answer
-
amplitude: none; period: \(\dfrac{2\pi }{5}\); no phase shift; asymptotes: \(x=\dfrac{\pi }{5}k\), where \(k\) is an integer
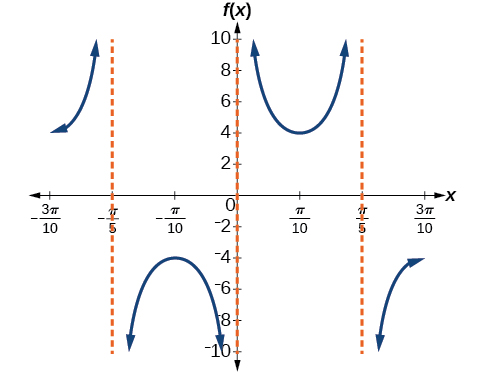
8) \(f(x)=8\sec \left (\dfrac{1}{4}x \right )\)
9) \(f(x)=\dfrac{2}{3}\csc \left (\dfrac{1}{2}x \right )\)
- Answer
-
amplitude: none; period: \(4\pi \); no phase shift; asymptotes: \(x=2\pi k\), where \(k\) is an integer
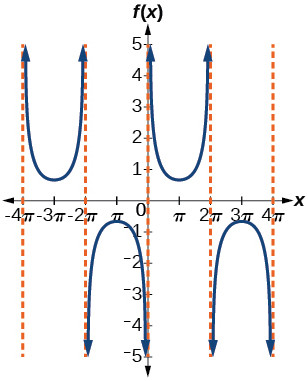
10) \(f(x)=-\csc (2x+\pi)\)
For the exercises 11-15, use this scenario: The population of a city has risen and fallen over a \(20\)-year interval. Its population may be modeled by the following function: \(y=12,000+8,000\sin(0.628x)\), where the domain is the years since 1980 and the range is the population of the city.
11) What is the largest and smallest population the city may have?
- Answer
-
largest: \(20,000\); smallest: \(4,000\)
12) Graph the function on the domain of \([0,40]\).
13) What are the amplitude, period, and phase shift for the function?
- Answer
-
amplitude: \(8,000\); period: \(10\); phase shift: \(0\)
14) Over this domain, when does the population reach \(18,000\)? \(13,000\)?
15) What is the predicted population in 2007? 2010?
- Answer
-
In 2007, the predicted population is \(4,413\). In 2010, the population will be \(11,924\).
For the exercises 16a-16d, suppose a weight is attached to a spring and bobs up and down, exhibiting symmetry.
16) Suppose the graph of the displacement function is shown in the Figure below, where the values on the \(x\)-axis represent the time in seconds and the \(y\)-axis represents the displacement in inches.
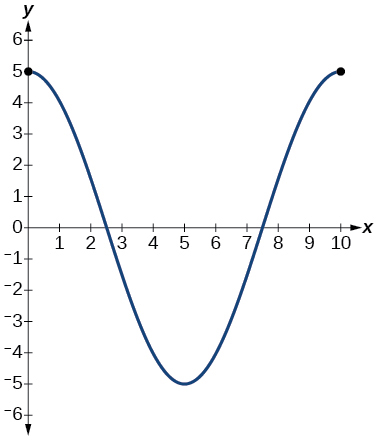
- Give the equation that models the vertical displacement of the weight on the spring.
- At \(\text{time} = 0\), what is the displacement of the weight?
- Answer
-
\(5\) in.
- At what time does the displacement from the equilibrium point equal zero?
- What is the time required for the weight to return to its initial height of \(5\) inches? In other words, what is the period for the displacement function?
- Answer
-
\(10\) seconds
6.3: Inverse Trigonometric Functions
For the exercises 1-11, find the exact value without the aid of a calculator.
1) \(\sin ^{-1}(1)\)
2) \(\cos ^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )\)
- Answer
-
\(\dfrac{\pi }{6}\)
3) \(\tan ^{-1}(-1)\)
4) \(\cos ^{-1}\left ( \dfrac{1}{\sqrt{2}} \right )\)
- Answer
-
\(\dfrac{\pi }{4}\)
5) \(\sin ^{-1}\left ( \dfrac{-\sqrt{3}}{2} \right )\)
6) \(\sin ^{-1}\left (\cos \left (\dfrac{\pi }{6} \right ) \right )\)
- Answer
-
\(\dfrac{\pi }{3}\)
7) \(\cos ^{-1}\left (\tan \left (\dfrac{3\pi }{4} \right ) \right )\)
8) \(\sin \left (\sec^{-1} \left (\dfrac{3}{5} \right ) \right )\)
- Answer
-
No solution
9) \(\cot \left (\sin^{-1} \left (\dfrac{3}{5} \right ) \right )\)
10) \(\tan \left (\cos^{-1} \left (\dfrac{5}{13} \right ) \right )\)
- Answer
-
\(\dfrac{12}{5}\)
11) \(\sin \left (\cos^{-1} \left (\dfrac{x}{x+1} \right ) \right )\)
12) Graph \(f(x)=\cos x\) and \(f(x)=\sec x\) on the interval \([0,2\pi )\) and explain any observations.
- Answer
-
The graphs are not symmetrical with respect to the line \(y=x\).
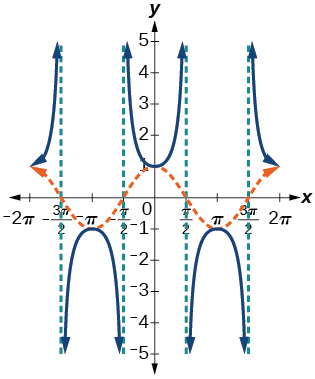
13) Graph \(f(x)=\sin x\) and \(f(x)=\csc x\) and explain any observations.
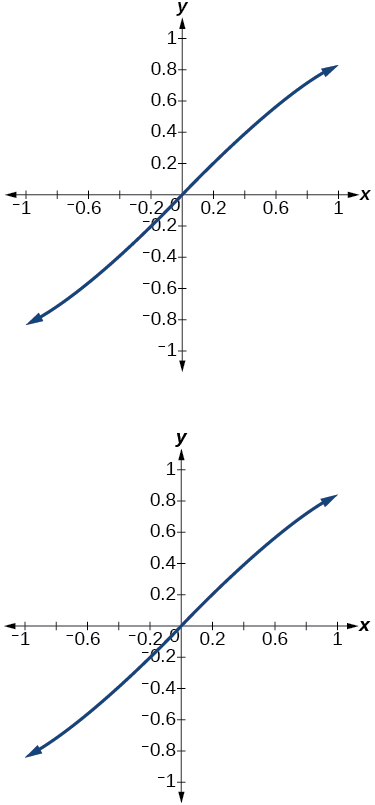
14) Graph the function \(f(x)=\dfrac{x}{1}-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}\) on the interval \([-1,1]\) and compare the graph to the graph of \(f(x)=\sin x\) on the same interval. Describe any observations.
- Answer
-
The graphs appear to be identical.
Practice Test
For the exercises 1-13, sketch the graph of each function for two full periods. Determine the amplitude, the period, and the equation for the midline.
1) \(f(x)=0.5\sin x\)
- Answer
-
amplitude: \(0.5\); period: \(2\pi \)
; 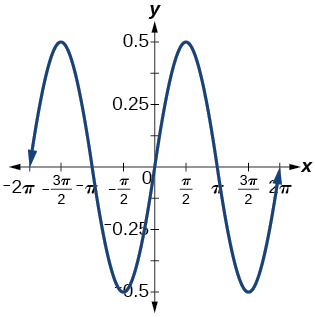 y=0
y=0 y = 0 y = 0
2) \(f(x)=5\cos x\)
3) \(f(x)=5\sin x\)
- Answer
-
amplitude: \(0.5\); period: \(2\pi \); midline \(y=0\)
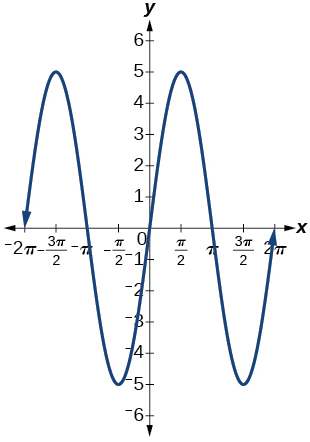
4) \(f(x)=\sin (3x)\)
5) \(f(x)=-\cos \left ( x+\dfrac{\pi }{3} \right )+1\)
- Answer
-
amplitude: \(1\); period: \(2\pi \); midline \(y=1\)
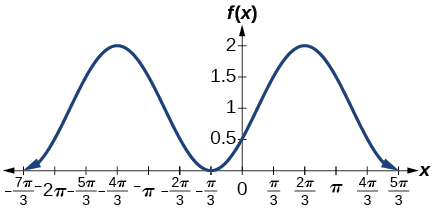
6) \(f(x)=5\sin \left (3\left ( x-\dfrac{\pi }{6} \right ) \right )+4\)
7) \(f(x)=3\cos \left ( \dfrac{1}{3}x-\dfrac{5\pi }{6} \right )\)
- Answer
-
amplitude: \(3\); period: \(6\pi \); midline \(y=0\)
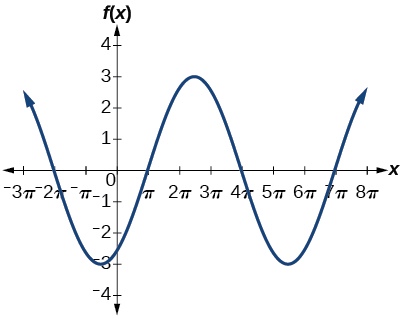
8) \(f(x)=\tan (4x)\)
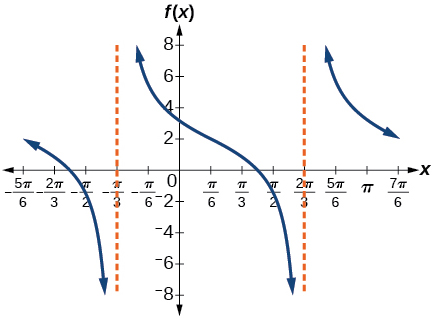
9) \(f(x)=-2\tan \left ( x-\dfrac{7\pi }{6} \right )+2\)
- Answer
-
amplitude: none; period: \(\pi \); midline \(y=0\), asymptotes: \(x=\dfrac{2\pi }{3}+\pi k\)
, 
10) \(f(x)=\pi \cos(3x+\pi)\)
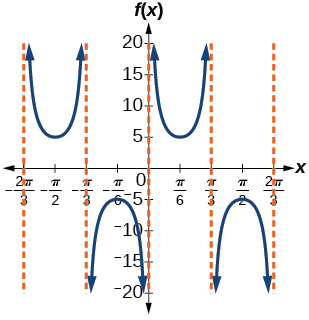
11) \(f(x)=5\csc(3x)\)
- Answer
-
amplitude: none; period: \(\dfrac{2\pi }{3}\); midline \(y=0\), asymptotes: \(x=\dfrac{\pi }{3}k\)
, 
12) \(f(x)=\pi \sec \left ( \dfrac{\pi }{2}x \right )\)
13) \(f(x)=2\csc \left ( x+\dfrac{\pi }{4} \right )-3\)
- Answer
-
amplitude: none; period: \(2\pi \); midline \(y=-3\)
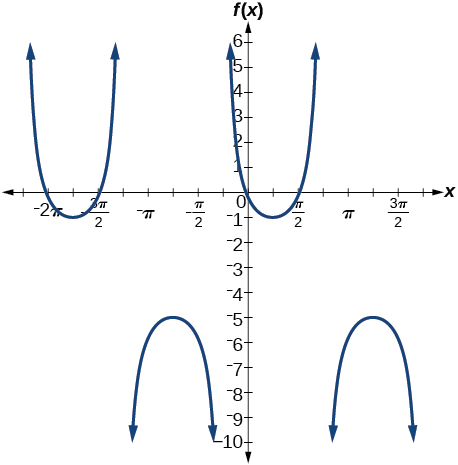
For the exercises 14-16, determine the amplitude, period, and midline of the graph, and then find a formula for the function.
14) Give in terms of a sine function.
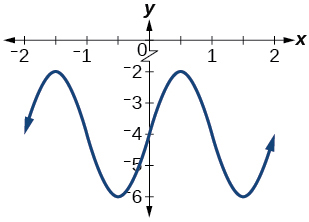
15) Give in terms of a sine function.
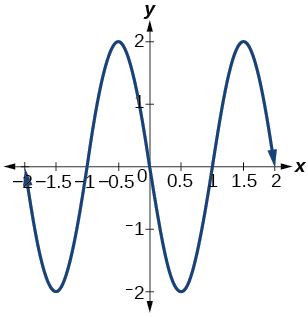
- Answer
-
amplitude: \(2\); period: \(2\); midline: \(y=0\); \(f(x)=2\sin(\pi (x-1))\)
16) Give in terms of a tangent function.
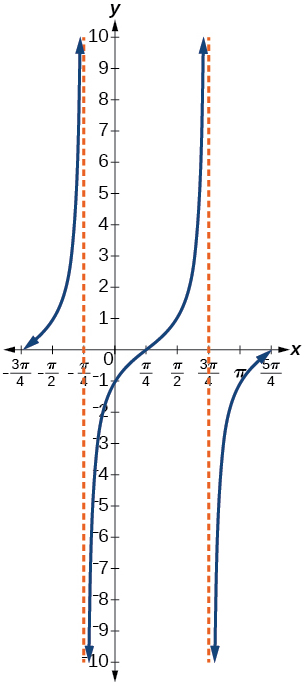
For the exercises 17-20, find the amplitude, period, phase shift, and midline.
17) \(y=\sin\left(\dfrac{\pi}{6}x+\pi \right)-3\)
- Answer
-
amplitude: \(1\); period: \(12\); phase shift: \(-6\); midline: \(y=-3\)
18) \(y=8\sin\left(\dfrac{7\pi}{6}x+\dfrac{7\pi}{2} \right)+6\)
19) The outside temperature over the course of a day can be modeled as a sinusoidal function. Suppose you know the temperature is \(68^{\circ}\)F at midnight and the high and low temperatures during the day are \(80^{\circ}\)F and \(56^{\circ}\)F, respectively. Assuming \(t\) is the number of hours since midnight, find a function for the temperature, \(D\), in terms of \(t\).
- Answer
-
\(D(t)=68-12\sin\left(\dfrac{\pi}{12}x \right)\)
20) Water is pumped into a storage bin and empties according to a periodic rate. The depth of the water is \(3\) feet at its lowest at 2:00 a.m. and \(71\) feet at its highest, which occurs every \(5\) hours. Write a cosine function that models the depth of the water as a function of time, and then graph the function for one period.
For the exercises 21-25, find the period and horizontal shift of each function.
21) \(g(x)=3\tan(6x+42)\)
- Answer
-
period: \(\dfrac{\pi}{6}\); horizontal shift: \(-7\)
22) \(n(x)=4\csc \left(\dfrac{5\pi }{3}x-\dfrac{20\pi }{3} \right)\)
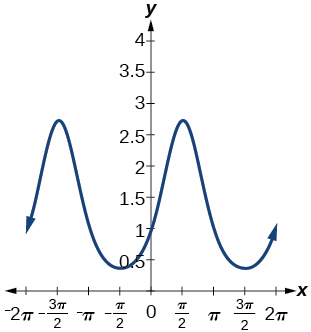
23) Write the equation for the graph in the Figure below in terms of the secant function and give the period and phase shift.
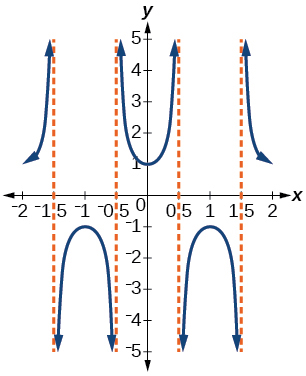
- Answer
-
\(f(x)=\sec(\pi x)\); period: \(2\); phase shift: \(0\)
24) If \(\tan x=3\)
25) If \(\sec x=4\), find \(\sec (-x)\).
- Answer
-
\(4\)
For the exercises 26-28, graph the functions on the specified window and answer the questions.
26) Graph \(m(x)=\sin(2x)+\cos(3x)\) on the viewing window \([-10,10]\) by \([-3,3]\)
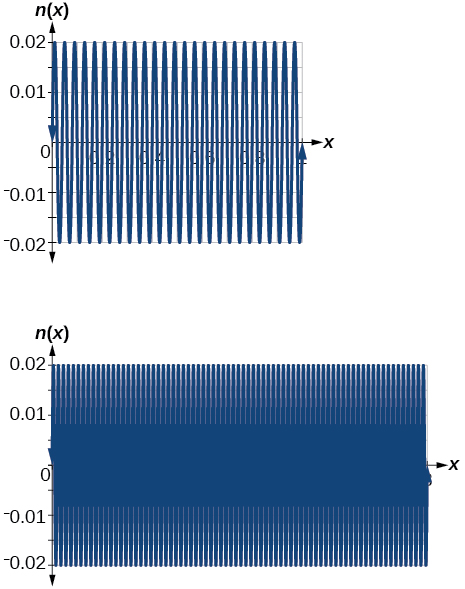
27) Graph \(n(x)=0.02\sin(50\pi x)\) on the following domains in \(x:[0,1]\) and\([0,3]\)
- Answer
-
The views are different because the period of the wave is \(125\)
. 
28) Graph \(f(x)=\dfrac{\sin x}{x}\) on \([-0.5,0.5]\) and explain any observations.
For the exercises 29-31, let \(f(x)=\dfrac{3}{5}\cos(6x)\).
29) What is the largest possible value for \(f(x)\)?
- Answer
-
\(\dfrac{3}{5}\)
30) What is the smallest possible value for \(f(x)\)?
31) Where is the function increasing on the interval \([0,2\pi ]\)?
- Answer
-
On the approximate intervals \((0.5,1),(1.6,2.1),(2.6,3.1),(3.7,4.2),(4.7,5.2),(5.6,6.28)\)
For the exercises 32-33, find and graph one period of the periodic function with the given amplitude, period, and phase shift.
32) Sine curve with amplitude \(3\), period \(\dfrac{\pi }{3}\)
33) Cosine curve with amplitude \(2\), period \(\dfrac{\pi }{6}\)
- Answer
-
\(f(x)=2\cos\left ( 12\left ( x+\dfrac{\pi }{4} \right ) \right )+3\)
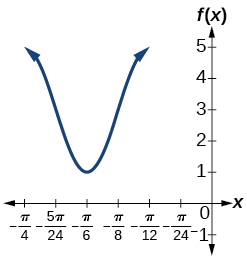
For the exercises 34-35, graph the function. Describe the graph and, wherever applicable, any periodic behavior, amplitude, asymptotes, or undefined points.
34) \(f(x)=5\cos(3x)+4\sin(2x)\)
35) \(f(x)=e^{(sint)}\)
- Answer
-
This graph is periodic with a period of \(2\pi \)
For the exercises 36-43, find the exact value.
36) \(\sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )\)
37) \(\tan^{-1}\left ( \sqrt{3} \right )\)
- Answer
-
\(\dfrac{\pi }{3}\)
38) \(\cos^{-1}\left ( -\dfrac{\sqrt{3}}{2} \right )\)
39) \(\cos^{-1}\left ( \sin(\pi) \right )\)
- Answer
-
\(\dfrac{\pi }{2}\)
40) \(\cos^{-1}\left ( \tan \left (\dfrac{7\pi}{4} \right ) \right )\)
41) \(\cos(\sin^{-1}(1-2x))\)
- Answer
-
\(\sqrt{1-(1-2x)^2}\)
42) \(\cos^{-1}(-0.4)\)
43) \(\cos \left (\tan^{-1}\left(x^2\right) \right )\)
- Answer
-
\(\dfrac{1}{\sqrt{1+x^4}}\)
For the exercises 44-46, suppose \(\sin t=\dfrac{x}{x+1}\)
44) \(\tan t\)
45) \(csc t\)
- Answer
-
\(\dfrac{x+1}{x}\)
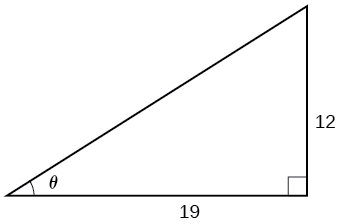
46) Given Figure, find the measure of angle \(\theta \) to three decimal places. Answer in radians.
For the exercises 47-49, determine whether the equation is true or false.
47) \(\arcsin\left(\sin\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}\)
- Answer
-
False
48) \(\arccos\left(\cos\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}\)
49) The grade of a road is \(7\%\). This means that for every horizontal distance of \(100\) feet on the road, the vertical rise is \(7\) feet. Find the angle the road makes with the horizontal in radians.
- Answer
-
approximately \(0.07\) radians


