10.2: Complex Numbers

So far most of your work in mathematics has been done using the set of real numbers. We often represent the real numbers by a number line, because they can be matched up one-for-one with the points on the line. Every real number is either rational or irrational, and can be expressed as a decimal number, although irrational numbers are non-repeating, non-terminating decimals. However, the real numbers are actually a subset of a larger set of numbers called the complex numbers.

You may have first encountered complex numbers as solutions of certain quadratic equations. For example, the graph of

\(f(x)=x^2-2 x+2\)

has no \(x\)-intercepts (as shown below), because the equation \(x^2-2 x+2-0\) has no real-valued solutions.

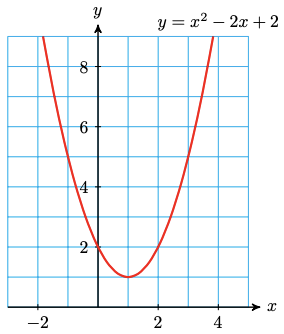
Applying the quadratic formula, we find

\(x=\dfrac{-(-2) \pm \sqrt{(-2)^2-4(1)(2)}}{2}=\dfrac{2 \pm \sqrt{-4}}{2}\)

The solutions of the equation are \(\frac{2+\sqrt{-4}}{2}\) and \(\frac{2-\sqrt{-4}}{2}\), but they are not real numbers. Because \(\sqrt{-4}\) is not a real number, the equation \(x^2-2 x+2-0\) has no real solutions.

Imaginary Numbers

Although square roots of negative numbers such as are not real numbers, they occur often in mathematics and its applications. Mathematicians began working with square roots of negative numbers in the sixteenth century, in their attempts to solve quadratic and cubic equations. René Descartes gave them the name imaginary numbers, which reflected the mistrust with which mathematicians regarded them at the time. Today, however, such numbers are well understood and used routinely by scientists and engineers

We begin by defining a new number, called \(i\), whose square is −1.

Imaginary Unit.

We define the imaginary unit, \(i\), by

\(i^2=-1 \quad \text { or } \quad i=\sqrt{-1}\)

The letter \(i\) used in this way is not a variable, it is the name of a specific number, and hence is a constant. The square root of any negative number can be written as the product of a real number and \(i\). For example,

\begin{aligned}
\sqrt{-4} & =\sqrt{-1 \cdot 4} \\
& =\sqrt{-1} \sqrt{4}=i \cdot 2
\end{aligned}

or \(\sqrt{-4}=2\). Any number that is the product of \(i i\) and a real number is called an imaginary number.

Imaginary Numbers.

For any real number \(a > 0\),

\(\sqrt{-a}=\sqrt{-1} \sqrt{a}=i \sqrt{a}\)

Examples of imaginary numbers are \(3 i, \frac{7}{8} i,-38 i\), and \(i \sqrt{5}\).

Example 10.32

Write each radical as an imaginary number.

a \(\sqrt{-25}\)

b \(2 \sqrt{-3}\)

Answer

a \(\sqrt{-25}=\sqrt{-1} \sqrt{25}=i \sqrt{25}=5 i\)

b \(2 \sqrt{-3}=\sqrt{-1} \sqrt{3}=2 i \sqrt{3}\)

Checkpoint 10.33

Write each radical as an imaginary number.

a \(\sqrt{-18}\)

b \(-6 \sqrt{-5}\)

Answer

a \(3 i \sqrt{2}\)

b \(-6 i \sqrt{5}\)

Just as each positive number has two real-valued square roots, every negative number has two imaginary square roots. For example, the two square roots of 9 are \(3 i\) and \(-3 i\).

Complex Numbers

Consider the quadratic equation

\(x^2-2 x+5=0\)

Using the quadratic formula to solve the equation, we find

\(x=\dfrac{-(-2) \pm \sqrt{(-2)^2-4(1)(5)}}{2}=\dfrac{2 \pm \sqrt{-16}}{2}\)

If we now replace \(\sqrt{-16}\) by \(4 i\), we have

\(x=\dfrac{2 \pm 4 i}{2}=1 \pm 2 i\)

The two solutions are \(1+2 i\) and \(1-2 i\). These are examples of complex numbers.

Complex Numbers.

A complex number can be written in the form

\(z=a+b i\)

where \(a\) and \(b\) are real numbers.

Examples of complex numbers are

\(3-5 i, 2+\sqrt{7} i, \dfrac{4-i}{3}, 6 i, \text { and }-9\)

In a complex number \(a+b i, a\) is called the real part, and \(b\) is called the imaginary part. All real numbers are also complex numbers (with imaginary part equal to zero). A complex number whose real part equals 0 is called a pure imaginary number.

The real and imaginary parts of a complex number cannot be combined. Thus, two complex numbers \(z_1\) and \(z_2\) are equal if and only if their real parts are equal and their imaginary parts are equal.

Equality of Complex Numbers.

Two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) are equal if and only if

\(a=c \text { and } c=d\)

Example 10.34

The solutions of the equation \(x^2-2 x+2=0\) are \(\frac{2 \pm \sqrt{-4}}{2}\). Write these solutions as complex numbers, and simplify.

Answer

Because \(\sqrt{-4}=\sqrt{-1} \sqrt{4}=2 i\), we have \(\frac{2 \pm \sqrt{-4}}{2}=\frac{2 \pm 2 i}{2}\), or \(1 \pm i\). The solutions are \(1+i\) and \(1-i\).

Checkpoint 10.35

Use extraction of roots to solve \((2 x+1)^2+9=0\). Write your answers as complex numbers.

Answer

\(x=\dfrac{-1}{2} \pm \dfrac{3}{2} i\)

Arithmetic of Complex Numbers

We add and subtract complex numbers by combining their real and imaginary parts separately. For example,

\begin{aligned}
(4+5 i)+(2-3 i) & =(4+2)+(5-3) i \\
& =6+2 i
\end{aligned}

The algebraic form of this rule can be stated as follows.

Sum and Difference of Complex Numbers.

The sum of two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) is

\(z_1+z_2=(a+b i)+(c+d i)=(a+c)+(b+d) i\)

Their difference is

\(z_1-z_2=(a+b i)-(c+d i)=(a-c)+(b-d) i\)

Example 10.36

Subtract: \((8-6 i)-(5+2 i)\).

Answer

Combine the real and imaginary parts.

\begin{aligned}
(8-6 i)-(5+2 i) & =(8-5)+(-6-2) i \\
& =3+(-8) i=3-8 i
\end{aligned}

Checkpoint 10.37

Subtract: \((-3+2 i)-(-3-2 i)\)

Answer

\(4i\)

Products of Complex Numbers

To find the product of two imaginary numbers, we use the fact that \(i^2=-1\). For example,

\begin{aligned}
(3 i)(4 i) & =3 \cdot 4 i^2 \\
& =12(-1)=-12
\end{aligned}

To find the product of two complex numbers, we use the distributive law, as if the numbers were binomials.

Example 10.38

Multiply \((2+3 i)(3-5 i)\).

Answer

We multiply each term of the first complex number by each term of the second one.

\((2+3 i)(3-5 i)=6-10 i+9 i-15 i^2\)

Because \(i^2=-1\), the last term, \(-15 i^2\), can be replaced by \(-15(-1)\), or \(15\), to obtain

\(6-10 i+9 i+15\)

Finally, we combine the real parts and imaginary parts to obtain

\((6+15)+(-10 i+9 i)=21-i\)

Checkpoint 10.39

Multiply \((-3+2 i)(-3-2 i)\).

Answer

13

In the Homework Probems, you will verify that the following rule holds.

Product of Complex Numbers.

The product of two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) is

\(z_1 z_2=(a+b i)(c+d i)=(a c-b d)+(a d+b c) i\)

Caution 10.40

One property of real numbers that is not true of complex numbers is \(\sqrt{a b}=\sqrt{a} \sqrt{b}\). This identity fails when \(a\) and \(b\) are both negative. For example, if \(a=b=-2\), we have

\(\sqrt{a b}=\sqrt{(-2)(-2)}=\sqrt{4}=2\)

but

\begin{aligned}
\sqrt{a} \cdot \sqrt{b} & =\sqrt{(-2)} \cdot \sqrt{(-2)} \\
& =\sqrt{(-1 \cdot 2)} \cdot \sqrt{(-1 \cdot 2)} \\
& =i \sqrt{2} \cdot i \sqrt{2}=i^2(\sqrt{2})^2=-2
\end{aligned}

so \(\sqrt{a b} \neq \sqrt{a} \sqrt{b}\). We can avoid possible errors by writing the square roots of negative numbers as imaginary numbers before attempting any calculations.

Quotients of Complex Numbers

To find the quotient of two complex numbers, we use the technique of rationalizing the denominator. First consider division by a pure imaginary number.

Example 10.41

Divide \(\dfrac{3+4 i}{2 i}\).

Answer

Because \(i\) is really a radical (remember that \(i=\sqrt{-1}\)), we multiply the numerator and denominator of the quotient by \(i\) to obtain

\begin{aligned}
\dfrac{(3+4 i) \cdot i}{2 i \cdot i} & =\dfrac{3 i+4 i^2}{2 i^2} \quad \quad &&\text{Apply the distributive law}.\\
& =\dfrac{3 i-4}{-2} \quad \quad &&\text{Recall that } i^2= -\mathbf{1}.
\end{aligned}

To write the quotient in the form \(a+b i\), we divide -2 into each term of the numerator.

\(\dfrac{3 i}{-2}-\dfrac{4}{-2}=\dfrac{-3}{2} i+2\)

The quotient is \(2-\dfrac{3}{2} i\).

Checkpoint 10.42

Divide \(\dfrac{8+9 i}{3 i}\).

Answer

\(3-\dfrac{8}{3} i\)

Perhaps you recall that to rationalize a binomial denominator, we multiply by its conjugate. For example, to rationalize the denominator of \(\frac{5}{2+\sqrt{3}}\), we multiply numerator and denominator by \(2-\sqrt{3}\). A similar technique works for dividing complex numbers. We first define the conjugate of a complex number.

Definition 10.43 Complex Conjugate.

For any complex number \(z=a+b i\), the number

\(\bar{z}=a-b i\)

is called the complex conjugate of \(z\).

Note 10.44 The conjugate of a complex number has several useful properties. In particular, the product of a nonzero complex number and its conjugate is always a positive real number.

\(z \bar{z}=(a+b i)(a-b i)=a^2-b^2 i^2=a^2-b^2(-1)=a^2+b^2\)

To illustrate, we calculate the quotient \(\frac{5}{2+3 i}\). We multiply numerator and denominator by the complex conjugate of the denominator, \(2-3 i\), to obtain

\(\dfrac{5}{2+3 i} \cdot \dfrac{2-3 i}{2-3 i}\)

The denominator is then a real number, because

\((2+3 i)(2-3 i)=4-6 i+6 i-9 i^2=4+9=13\)

and the quotient is

\(\dfrac{5}{2+3 i} \cdot \dfrac{2-3 i}{2-3 i}=\dfrac{10-15 i}{13}=\dfrac{10}{13}-\dfrac{15}{13} i\)

Example 10.45

Divide \(\dfrac{2+3 i}{4-2 i}\).

Answer

We multiply the numerator and denominator by \(4+2 i\), the complex conjugate of the denominator.

\begin{aligned}
\dfrac{2+3 i}{4-2 i} & =\dfrac{(2+3 i)(4+2 i)}{(4-2 i)(4+2 i)} \quad \quad &&\text{Expand numerator and denominator.} \\
& =\dfrac{8+4 i+12 i+6 i^2}{16+8 i-8 i-4 i^2} \quad \quad &&\text{Replace } i^2 \text{ by }-\mathbf{1}.\\
& =\dfrac{8+16 i-6}{16-(-4)} \quad \quad &&\text{Combine like terms.}\\
& =\dfrac{2+16 i}{20} \quad \quad &&\text{Divide 20 into each term of numerator.}\\
& =\dfrac{2}{20}+\dfrac{16 i}{20}=\dfrac{1}{10}+\dfrac{4}{5} i
\end{aligned}

Checkpoint 10.46

Write the quotient \(\frac{4-2 i}{1+i}\) in the form \(a+b i\).

Answer

\(1-3 i\)

In the Homework Problems you will verify the rule for dividing complex numbers.

Quotient of Complex Numbers.

The quotient of two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) is

\(\dfrac{z_1}{z_2}=\dfrac{a+b i}{c+d i}=\dfrac{a+b i}{c+d i} \cdot \dfrac{c-d i}{c-d i}=\dfrac{a c+b d}{c^2+d^2}+\dfrac{b c-a d}{c^2+d^2} i\)

Graphing Complex Numbers

Real numbers can be plotted on a number line, but to graph a complex number we use a plane, called the complex plane. In the complex plane, the real numbers lie on the horizontal or real axis, and pure imaginary numbers lie on the vertical or imaginary axis. To plot a complex number \(a+b i\) we move \(a\) units from the origin in the horizontal direction and \(b\) units in the vertical direction.

Example 10.47

Plot the numbers \(z=2+3 i\) and \(\bar{z}=2-3 i\) in the complex plane.

Answer

To plot \(z=2+3 i\), we move from the origin 2 units to the right and 3 units up. To plot \(\bar{z}=2-3 i\) we move from the origin 2 units to the right and 3 units down. The numbers \(2+3 i\) and \(2-3 i\) are plotted in the figure below.

Checkpoint 10.48

Plot \(z=-3+5 i\) and its conjugate in the complex plane.

Answer

Caution 10.49

You are used to plotting ordered pairs \((x, y)\) in the Cartesian plane, so that one point represents two real numbers, given by its coordinates. However, in the complex plane one point represents a single complex number \(z=a+b i\), and the coordinates of the point are the real and imaginary parts of \(z\). For example, the point (2,-6) in the real plane represents the pair of real numbers \(x=2\) and \(t=-6\), but the point (2,-6) in the complex plane represents the complex number \(z=2-6 i\).

The modulus, or length, of a complex number is its distance from the origin in the complex plane. The modulus of a complex number is analogous to the absolute value of a real number, and is denoted by \(|z|\). If \(z=a+b i\), we can use the Pythagorean theorem to compute its modulus.

Modulus of a Complex Number.

The modulus of a complex number \(z=a+b i\) is given by

\(|z|=\sqrt{a^2+b^2}\)

For example, the modulus of \(z=2+3 i\) is

\(|z|=\sqrt{2^2+3^2}=\sqrt{13}\)

Example 10.50

Plot all points in the complex plane that satisfy the equation \(|z|=4\).

Answer

The points that satisfy \(|z|=4\) all lie at a distance of 4 units from the origin. In other words, they lie on a circle of radius 4 centered at the origin, as shown below.

Checkpoint 10.51

Write an equation for the circle of radius 1 centered at the origin in the complex plane.

Answer

\(|z|=1\)

We can think of the graph of a complex number \(z=a+b i\) as the vector (or arrow) that starts at the origin and ends at the point \((a, b)\) in the complex plane, as shown in figure (a).

Then the sum of two complex numbers corresponds to the sum of the two vectors representing them. Figure (b) illustrates the sum of two complex numbers, \(z_1\) and \(z_2\), by vector addition using the parallelogram law: we form a parallelogram with the vectors \(z_1\) and \(z_2\) and as adjacent sides. Their sum is the vector that forms the diagonal of the parallelogram, starting at the origin.

Example 10.52

Illustrate the sum of \(z_1=5-i\) and \(z_2=-7+4 i\) by vector addition.

Answer

Draw a vector starting at the origin and ending at the point (5,-1) in the complex plane to represent \(z_1\), and another vector ending at (-7,4) to represent \(z_2\). Now sketch the opposite sides of a parallelogram, and draw the diagonal starting at the origin, as shown below.

This vector represents the sum \(z_1+z_2\). You can check that the vector ends at the point

\(z_1+z_2=(5-7)+(-1+4) i=-2+3 i\)

To visualize subtraction, we add the opposite of the second vector, because

\(z_1-z_2=z_1+\left(-z_2\right)\)

Recall that the opposite of a vector has the same length, but it points in the opposite direction.

Checkpoint 10.53

Illustrate \(z_1-z_2\), for \(z_1=3-2 i\) and \(z_2=-4+5 i\).

Answer

Zeros of Polynomials

A polynomial with real-number coefficients may or may not have real-valued zeros. For example, the polynomial \(x^4+4\) has no real-valued zeros. But a polynomial always has a zero if we allow complex numbers as inputs. Because we can add, subtract, and multiply any two complex numbers, we can evaluate a polynomial function at a complex number. Thus, we can extend the domain of any polynomial to include all complex numbers.

Example 10.54

Evaluate the polynomial \(f(x)=x^2-2 x+2\) for \(x=1+i\), and simplify.

Answer

We substitute \(x=1+i\), to find

\begin{aligned}
f(1+i) & =(1+i)^2-2(1+i)+2 \\
& =1^2+2 i+i^2-2-2 i+2 \\
& =1+2 i+(-1)-2-2 i+2
\end{aligned}

Thus, \(f(1+i)=0\), so \(1+i\) is a zero of the polynomial.

Checkpoint 10.55

If \(f(x)=x^2-6 x+13\), evaluate \(f(3+2 i)\).

Answer

0

The zeros of a quadratic polynomial \(a x^2+b x+c\), of course, are the solutions of the quadratic equation \(a x^2+b x+c=0\), and those solutions are given by the quadratic formula,

\(x=\dfrac{-b}{2 a}+\dfrac{b^2-4 a c}{2 a} \text { and } x=\dfrac{-b}{2 a}-\dfrac{b^2-4 a c}{2 a}\)

If the discriminant \(D=b^2-4 a c\) is negative, the two solutions are complex conjugates. For example, the solutions of the equation \(x^2-4 x+5=0\) are

\(\dfrac{-(-4) \pm \sqrt{(-4)^2-4(1)(5)}}{2(1)}=\dfrac{4 \pm \sqrt{-4}}{2}\)

or \(z=2+i\) and \(\bar{z}=2-i\). Thus, if we know that \(z=a+b i\) is one complex solution of a quadratic equation, we know that \(\bar{z}=a-b i\) is the other solution.

We can now write a quadratic polynomial, with real coefficients, having any complex number as one of its zeros. The factored form of the quadratic polynomial with zeros \(z\) and \(\bar{z}\) is

\(p(x)=(x-z)(x-\bar{z})\)

Expanding the right side, we find

\(p(x)=x^2-(z+\bar{z}) x+z \bar{z}\)

Because \((z+\bar{z})\) and \(z \bar{z}\) are both real numbers, this polynomial has real-valued coefficients.

Complex Zeros of a Quadratic Polynomial.

If \(z=a+b i, b \neq 0\), is a complex zero of a quadratic polynomial \(p(x)\) with real coefficients, then \(\bar{z}=a-b i\) is the other zero, and

\(p(x)=(x-z)(x-\bar{z})=x^2-(z+\bar{z}) x+z \bar{z}\)

Example 10.56

a Let \(z=7-5 i\). Compute \((z+\bar{z})\) and \(z \bar{z}\).

b Find a quadratic polynomial with one zero being \(z=7-5 i\).

Answer

a The conjugate of \(z=7-5 i\) is \(\bar{z}=7+5 i\), so

\((z+\bar{z})=(7-5 i)+(7+5 i)=14\)

and

\begin{aligned}
z \bar{z} & =(7-5 i)(7+5 i) \\
& =49-25 i^2=49+25=74
\end{aligned}

b The polynomial is

\begin{aligned}
p(x) & =x^2+(z+\bar{z}) x+z \bar{z} \\
& =x^2-14 x+74
\end{aligned}

Checkpoint 10.57

a Let \(z=-3+4 i\). Compute \((z+\bar{z})\) and \(z \bar{z}\).

b Find a quadratic polynomial with one zero being \(z=-3+4 i\).

Answer

a \(z+\bar{z}=-6, \quad z \bar{z}=25\)

b \(x^2+6 x+25=0\)

One of the most important results in mathematics is the fundamental theorem of algebra, which says that if we allow complex numbers as inputs, then every polynomial \(p(x)\) of degree \(n \geq 1\) has exactly \(n\) complex number zeros.

Fundamental Theorem of Algebra.

Let \(p(x)\) be a polynomial of degree \(n \geq 1\). Then \(p(x)\) has exactly \(n\) complex zeros, counting multiplicities.

Note 10.58 A polynomial has a zero "of multiplicity \(k\)" at \(x=a\) if \((x-a)\) occurs \(k\) times as a factor of the polynomial. For example, the polynomial \(p(x)=(x-5)^2\) has a zero of multiplicity 2 at \(x=5\).

As a result, every polynomial of degree can be factored as the product of linear terms.

For example, although the graph of \(y=x^4+4\) shown below has no \(x\)-intercepts, the fundamental theorem tells us that there are four complex solutions to \(x^4+4=0\), and that \(x^4+4\) can be factored. You can check that the four solutions to \(x^4+4=0\) are

\(1+i,-1+i,-1-i\), and \(1-i\)

For example, if \(x=1+i\), then

\(x^2=(1+i)^2=1+2 i+i^2=2 i\)

and

\(x^4=\left(x^2\right)^2=(2 i)^2=-4\)

Because each zero corresponds to a factor of the polynomial, the factored form of \(x^4+4\) is

\(x^4+4=[x-(1+i)][x-(-1+i)][x-(-1-i)][x-(1-i)]\)

The four solutions to \(x^4+4=0\) form two complex conjugate pairs, namely \(1 \pm i\) and \(-1 \pm i\). We see again that, for every polynomial with real coefficients, the nonreal zeros always occur in complex conjugate pairs.

Example 10.59

Find a fourth degree polynomial with real coefficients, two of whose zeros are \(3 i\) and \(2+i\).

Answer

The other two zeros are \(-3 i\) and \(2-i\). The factored form of the polynomial is

\((x-3 i)(x+3 i)[x-(2+i)][x-(2-i)]\)

We multiply together the factors to find the polynomial. The product of \((x-3 i)(x+3 i)\) is \(x^2+9\), and

\begin{aligned}
{[x-(2+i)][x-(2-i)] } & =x^2-(2+i+2-i) x+(2+i)(2-i) \\
& =x^2-4 x+5
\end{aligned}

Finally, we multiply these two partial products to find the polynomial we seek,

\(\left(x^2+9\right)\left(x^2-4 x+5\right)=x^4-4 x^3+14 x^2-36 x+45\)

Checkpoint 10.60

a Find the zeros of the polynomial \(x^4+15 x^2-16\).

b Write the polynomial in factored form.

Answer

a \(\pm 1, \pm 4 i\)

b \((x-1)(x+1)(x-4 i)(x+4 i)\)

Review the following skills you will need for this section.

Algebra Refresher 10.3

Solve.

1 \(3x^2 = 6x\)

2 \(16x^2 = 9\)

3 \(x^2+4x = 12\)

4 \(2(x-3)^2 = 8\)

5 \(3x^2 - 8 = 10x\)

6 \(x^2 - 3x + 1 = 0\)

Algebra Refresher Answers

1 \(0, 2\)

2 \(\dfrac{\pm 3}{4}\)

3 \(-6,2\)

4 \(1,5\)

5 \(\dfrac{-2}{3}, 4\)

6 \(\dfrac{3 \pm \sqrt{5}}{2}\)

Section 10.3 Summary

Vocabulary

• Imaginary unit

• Imaginary number

• Complex number

• Complex conjugate

• Real part

• Imaginary part

• Complex plane

• Real axis

• Imaginary axis

• Modulus

Concepts

Imaginary Unit.

1 We define the imaginary unit, \(i\), by

\(i^2=-1 \quad \text { or } \quad i=\sqrt{-1}\)

2 The square root of a negative number is an imaginary number: if \(a>0, \sqrt{-a}=i \sqrt{a}\)

3 A complex number \(z\) is the sum of a real number and an imaginary number, \(z=a+b i\).

4 We can perform the four arithmetic operations on complex numbers.

Operations on Complex Numbers.

\begin{gathered}
z_1+z_2=(a+b i)+(c+d i)=(a+c)+(b+d) i \\
z_1-z_2=(a+b i)-(c+d i)=(a-c)+(b-d) i \\
z_1 z_2=(a+b i)(c+d i)=(a c-b d)+(a d+b c) i \\
\dfrac{z_1}{z_2}=\dfrac{a+b i}{c+d i}=\dfrac{a+b i}{c+d i} \cdot \dfrac{c-d i}{c-d i}=\dfrac{a c+b d}{c^2+d^2}+\dfrac{b c-a d}{c^2+d^2} i
\end{gathered}

5 The product of a nonzero complex number and its conjugate is always a positive real number.

\(z \bar{z}=(a+b i)(a-b i)=a^2-b^2 i^2=a^2-b^2(-1)=a^2+b^2 .\)

6 We can graph complex numbers in the complex plane.

7 We can visualize the sum of two complex numbers by vector addition in the complex plane.

Fundamental Theorem of Algebra.

8 Let \(p(x)\) be a polynomial of degree \(n \geq 1\). Then \(p(x)\) has exactly \(n\) complex zeros.

9 The nonreal zeros of a polynomial with real coefficients always occur in conjugate pairs.

Study Questions

1 What are imaginary numbers, and why were they invented?

2 Simplify the following powers of \(i\):

\(i^2, i^3, i^4, i^5, i^6, i^7, i^8\)

What do you notice?

3 Explain how the complex conjugate is used in dividing complex numbers.

4 If one solution of a quadratic equation is \(3+i \sqrt{2}\), what is the other solution?

5 If \(P(x)\) is a polynomial of degree 7, how many zeros does \(P(x)\) have? How many \(x\)-intercepts could its graph have? How many complex zeros could \(P(x)\) have?

Skills

1 Write and simplify complex numbers #1–6

2 Perform arithmetic operations on complex numbers #7–34

3 Evaluate polynomials at complex numbers, expand polynomials #35–46

4 Graph complex numbers #47–58

5 Find a polynomial with given zeros #67–74

Homework 10-3

For Problems 1-2, write the complex number in the form \(a+b i\), where \(a\) and \(b\) are real numbers.

1.

a \(\sqrt{-25}-4\)

b \(\dfrac{-8+\sqrt{-4}}{2}\)

c \(\dfrac{-5-\sqrt{-2}}{6}\)

2.

a \(\sqrt{-9}+3\)

b \(\frac{6-\sqrt{-36}}{2}\)

c \(\frac{7+\sqrt{-3}}{4}\)

For Problems 3-6, find the zeros of the quadratic polynomial. Write each zero in the form \(a+b i\), where \(a\) and \(b\) are real numbers.

3. \(x^2+6 x+13\)

4. \(x^2-2 x+10\)

5. \(3 x^2-x+1\)

6. \(5 x^2+2 x+2\)

For Problems 7–10, add or subtract.

7. \((11-4 i)-(-2-8 i)\)

8. \((7 i-2)+(6-4 i)\)

9. \((2.1+5.6 i)+(-1.8 i-2.9)\)

10. \(\left(\dfrac{1}{5} i-\dfrac{2}{5}\right)-\left(\dfrac{4}{5}-\dfrac{3}{5} i\right)\)

For Problems 11–20, multiply.

11. \(5 i(2-4 i)\)

12. \(-7 i(-1+4 i)\)

13. \((4-i)(-6+7 i)\)

14. \((2-3 i)(2-3 i)\)

15. \((7+i \sqrt{3})^2\)

16. \((5-i \sqrt{2})^2\)

17. \((7+i \sqrt{3})(7-i \sqrt{3})\)

18. \((5-i \sqrt{2})(5+i \sqrt{2})\)

19. \((1-i)^3\)

20. \((2+i)^3\)

For Problems 21–32, divide.

21. \(\dfrac{12+3 i}{-3 i}\)

22. \(\dfrac{12+4 i}{8 i}\)

23. \(\dfrac{10+15 i}{2+i}\)

24. \(\dfrac{4-6 i}{1-i}\)

25. \(\dfrac{5 i}{2-5 i}\)

26. \(\dfrac{-2 i}{7+2 i}\)

27. \(\dfrac{\sqrt{3}}{\sqrt{3}+i}\)

28. \(\dfrac{2 \sqrt{2}}{1-i \sqrt{2}}\)

29. \(\dfrac{1+i \sqrt{5}}{1-i \sqrt{5}}\)

30. \(\dfrac{\sqrt{2}-i}{\sqrt{2}+i}\)

31. \(\dfrac{3+2 i}{2-3 i}\)

32. \(\dfrac{4-6 i}{-3-2 i}\)

33. Simplify.

a \(i^6\)

b \(i^{12}\)

c \(i^{15}\)

d \(i^{102}\)

34. Express with a positive exponent and simplify.

a \(i^{-1}\)

b \(i^{-2}\)

c \(i^{-3}\)

d \(i^{-6}\)

For Problems 35-40, evaluate the polynomial for the given values of the variable.

35. \(z^2+9\)

a \(z=3 i\)

b \(z=-3 i\)

36. \(2 y^2-y-2\)

a \(y=2-i\)

b \(y=-2-i\)

37. \(x^2-2 x+2\)

a \(x=1-i\)

b \(x=1+i\)

38. \(3 w^2+5\)

a \(w=2 i\)

b \(w=-2 i\)

39. \(q^2+4 q+13\)

a \(q=-2+3 i\)

b \(q=-2-3 i\)

40. \(v^2+2 v+3\)

a \(v=1+i\)

b \(v=-1+i\)

For Problems 41–46, expand the product of polynomials.

41. \((2 z+7 i)(2 z-7 i)\)

42. \((5 w+3 i)(5 w-3 i)\)

43. \([x+(3+i)][x+(3-i)]\)

44. \([s-(1+2 i)][s-(1-2 i)]\)

45. \([v-(4+i)][v-(4-i)]\)

46. \([Z+(2+i)][Z+(2-i)]\)

For Problems 47–50, plot the number and its complex conjugate in the complex plane. What is the geometric relationship between complex conjugates?

47. \(z=-3+2 i\)

48. \(z=4-3 i\)

49. \(z=\dfrac{\sqrt{3}}{2}-\dfrac{1}{2} i\)

50. \(z=-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2} i\)

For Problems 51–54, sketch the set of points in the complex plane.

51. \(|z| \leq 2\)

52. \(1<|z|<3\)

53. The set of all \(z=a+b i\) for which \(a \geq b\)

54. The set of all \(z=a+b i\) for which \(a+b<2\)

For Problems 55–58, illustrate addition using the parallelogram rule in the complex plane.

55. \((1-4 i)+(-3+2 i)\)

56. \((-4+2 i)+(-2+i)\)

57. \((2+6 i)-(3+3 i)\)

58. \((-5-2 i)-(-3+2)\)

59. Prove that the product of two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) is

\(z_1 z_2=(a+b i)(c+d i)=(a c-b d)+(a d+b c) i\)

60. Prove that the quotient of two complex numbers \(z_1=a+b i\) and \(z_2=c+d i\) is

\(\dfrac{z_1}{z_2}=\dfrac{a+b i}{c+d i}=\dfrac{a+b i}{c+d i} \cdot \dfrac{c-d i}{c-d i}=\dfrac{a c+b d}{c^2+d^2}+\dfrac{b c-a d}{c^2+d^2} i\)

61. Prove the commutative laws for addition and multiplication of complex numbers:

\begin{aligned}
z_1+z_2 & =z_2+z_1 \\
z_1 z_2 & =z_2 z_1
\end{aligned}

62. Prove the distributive law for complex numbers:

\(z_1\left(z_2+z_3\right)=z_1 z_2+z_1 z_3\)

63.

a Show that \(z+\bar{z}\) is a real number, and \(z-\bar{z}\) is an imaginary number.

b Show that \(z \bar{z}=|z|^2\)

64. Show that \(\overline{z w}=\bar{z} \cdot \bar{w}\)

65. Suppose \(t, w\) and \(z\) are complex numbers. If \(w=t+z\), is it necessarily true that \(|w|=|t|+|z|\)? Provide examples to support your conclusion.

66. Prove the triangle inequality for complex numbers:

\(|w+z| \leq|w|+|z|\)

In Problems 67–70,

a Given one solution of a quadratic equation with rational coefficients, find the other solution.

b Write a quadratic equation that has those solutions.

67. \(2+\sqrt{5}\)

68. \(3-\sqrt{2}\)

69. \(4-3 i\)

70. \(5+i\)

For Problems 71–74, find a fourth degree polynomial with real coefficients that has the given complex numbers as two of its zeros.

71. \(1-3 i, 2-i\)

72. \(5-4 i,-i\)

73. \(\dfrac{1}{2}-\dfrac{\sqrt{3}}{2} i, 3+2 i\)

74. \(-\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} i, 4-i\)