10.1: Polar Graphs

Graphing in Polar Coordinates

When we plot points in Cartesian coordinates, we start at the origin and move a distance right or left given by the $x$-coordinate of the point, then move up or down according to the $y$-coordinate. When we sketch the graph of an equation or function, we think of drawing the graph from left to right, with the "height" of the graph at each $x$-value given by the function, as shown in figure (a).

In polar coordinates, however, the dependent variable, $r$, gives not a height but a distance from the pole in direction $\theta$, as shown in figure (b). When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle $\theta$ the $r$-value tells us how far the graph is from the pole.

Example 10.17

Graph the polar equation $r=2 \sin \theta$.

Answer

We make a table of values, choosing the special values for $\theta$. For each value of $\theta$, we evaluate $r=2 \sin \theta$.

$\theta$	0	$\dfrac{\pi}{6}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{3\pi}{4}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	0	1	$\sqrt{2}$	$\sqrt{3}$	2	$\sqrt{3}$	$\sqrt{2}$	1	0

First, we'll plot the points in the first quadrant. Observe that as $\theta$ increases from 0 to $\frac{\pi}{2}$, $r$ increases from 0 to 2. Starting at the pole, we connect the points in order of increasing $\theta$. Imagine a radial line sweeping around the graph through the first quadrant: as the angle increases, the length of the segment increases, so that its tip traces out the graph shown in figure (a).

Now continue plotting the points in the table as $\theta$ increases from $\frac{\pi}{2}$ to $\pi$. In the second quadrant, $r$ decreases as $\theta$ increases, as shown in figure (b). The graph we obtain is, in fact, a circle, which we will prove algebraically shortly. However, we have not yet plotted points for $\theta$ between 0 and $2 \pi$. Because $\sin \theta$ is negative in the third and fourth quadrants, all the $r$-values for these angles are negative.

$\theta$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{5\pi}{4}$	$\dfrac{4\pi}{3}$	$\dfrac{3\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{7\pi}{4}$	$\dfrac{11\pi}{6}$	$\pi$
$r$	0	-1	$-\sqrt{2}$	$-\sqrt{3}$	-2	$-\sqrt{3}$	$-\sqrt{2}$	-1	0

When we plot the points in this table, we see that the original graph is traced out again. For example, the point $\left(\frac{7 \pi}{6},-1\right)$ is the same as the point $\left(\frac{\pi}{6}, 1\right)$, the point $\left(\frac{5 \pi}{4},-\sqrt{2}\right)$ is the same as the point $\left(\frac{\pi}{4}, \sqrt{2}\right)$, and so on, around the circle. Thus, the graph of $r=2 \sin \theta$ is a circle, traced twice for $0 \leq \theta \leq 2 \pi$.

To prove that the graph in Example 1 is really a circle, we convert the equation $r=2 \sin \theta$ to Cartesian form. First, multiply both sides by $r$ to obtain

$r^2=2 r \sin \theta$

Next, replace $r^2$ by $x^2+y^2$ and $r \sin \theta$ by $y$, to get

$x^2+y^2=2 y$

This equation is quadratic in two variables, so its graph is a conic section. We put the equation in standard form by completing the square in $y$.

$$\begin{aligned} x^2+y^2-2 y&=0 \quad \quad &&\text{Add 1 to both sides.} \\ x^2+\left(y^2-2 y+1\right)&=1 \quad \quad &&\text{Write the equation in standard form.} \\ (x-0)^2+(y-1)^2&=1 \end{aligned}$$

We have the equation of a circle with center (0, 1) and radius 1.

Checkpoint 10.18

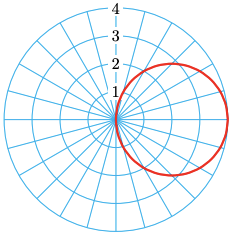
Graph the polar equation $r=4 \cos \theta$.

Answer

Using a Graphing Calculator

You are familiar with the graphs of many equations in Cartesian coordinates, including lines, parabolas and other conic sections, and the graphs of basic functions. You should now become familiar with some standard graphs in polar coordinates. These include circles and roses, cardioids and limaçons, lemniscates, and spirals.

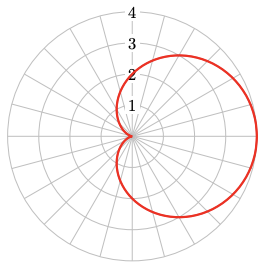
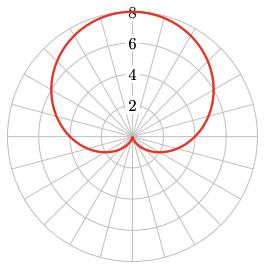
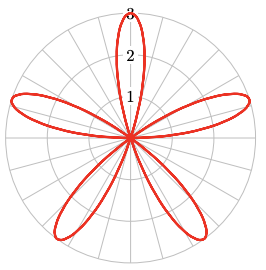
At the end of this section you will find a Catalog of the basic polar graphs and their properties. You can use your calculator, set in Polar mode, to experiment with these graphs.

Example 10.19

Graph the Archimedean spiral $r=2 \theta$, for $0 \leq \theta \leq 6 \pi$.

Answer

After setting the calculator in Polar mode, we enter the equation $r=2 \theta$ and enter the window settings

$\begin{array}{ccc} \theta \min =0 & \theta \max =6 \pi & \theta \text { step }=0.1 \\ \mathrm{Xmin}=-25 & \mathrm{Xmax}=25 & \mathrm{X} \text { step }=5 \\ \mathrm{Ymin}=-25 & \mathrm{Ymax}=25 & \mathrm{Yscl}=5 \end{array}$

We then press Zoom 5 to set a square window.

The graph is shown below.

Studying a table of values can help us understand the shape of the graph.

$\theta$	0.25	0.50	0.75	1.00	1.25
$r$	0.50	1.00	1.50	2.00	2.50

As $\theta$ increases, $r$ increases also, at a constant rate. We wind our way around the pole, steadily increasing our distance from the pole as we go. We spiral outwards, tracing the graph shown above.

Checkpoint 10.20

Use a calculator to graph the polar equation $r=e^{0.1 \theta}$. Use the window settings

$\begin{array}{ccc} \theta \min =0 & \theta \max =12 \pi & \theta \text { step }=0.5 \\ \mathrm{Xmin}=-45 & \mathrm{Xmax}=45 & \text { Xstep }=10 \\ \mathrm{Ymin}=-35 & \mathrm{Ymax}=35 & \text { Yscl }=10 \end{array}$

Answer

It is important to connect the points on the graph in order of increasing $\theta$.

Example 10.21

Graph the polar equation $r=2 \sin 3 \theta$.

Answer

We’ll graph the equation in stages in order to see how the graph is traced out. Begin with the window settings

$$\begin{aligned} & \theta \min =0 \quad \theta \max =\frac{\pi}{3} \quad \theta \text { step }=0.5 \\ & \mathrm{Xmin}=-4.5 \quad \mathrm{Xmax}=4.5 \quad \text { Xstep }=1 \\ & \mathrm{Ymin}=-3 \quad \mathrm{Ymax}=3 \quad \mathrm{Yscl}_{=1} \\ \end{aligned}$$

Watch as your calculator produces the graph shown in figure (a).

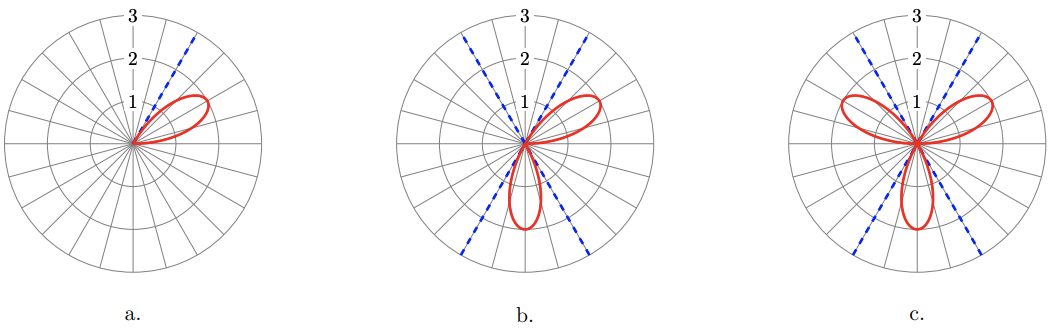
Observe that, as $\theta$ increases from 0 to $\frac{\pi}{3}, r$ first increases, reaching its maximum value of 2 at $\theta=\frac{\pi}{6}$ and then decreases back to 0. You can verify the values in the table below, which shows the points at multiples of $\frac{\pi}{18}$. These points create the first loop of the graph.

$\theta$	0	$\dfrac{\pi}{18}$	$\dfrac{\pi}{9}$	$\dfrac{\pi}{6}$	$\dfrac{2\pi}{9}$	$\dfrac{5\pi}{18}$	$\dfrac{\pi}{3}$
$3\theta$	0	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$
$r$	0	1	$\sqrt{3}$	2	$\sqrt{3}$	1	0

Next, change $\theta \max$ to $\frac{2 \pi}{3}$, and graph again. This time the calculator traces out two loops, as shown in figure (b). For $\theta$ between $\frac{\pi}{3}$ and $\frac{2 \pi}{3}, r$ is negative, so the second loop lies in the third and fourth quadrants.

$\theta$	$\dfrac{\pi}{3}$	$\dfrac{7\pi}{18}$	$\dfrac{4\pi}{9}$	$\dfrac{\pi}{2}$	$\dfrac{5\pi}{9}$	$\dfrac{11\pi}{18}$	$\dfrac{2\pi}{3}$
$3\theta$	$\pi$	$\dfrac{7\pi}{6}$	$\dfrac{4\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{5\pi}{3}$	$\dfrac{11\pi}{6}$	$2\pi$
$r$	0	-1	$-\sqrt{3}$	-2	$-\sqrt{3}$	-1	0

Finally, change $\theta \max$ to $\pi$, and graph again. For $\theta$ between $\frac{2 \pi}{3}$ and $\pi$, the graph traces out a third loop, as shown in figure (c). For $\theta$ between $\pi$ and $2 \pi$, the entire graph is traced a second time. The finished graph is a rose with 3 petals of length 2.

Checkpoint 10.22

a Use your calculator to graph the polar equation $r=2 \cos 3 \theta$.

b Complete the table of values for the function.

$\theta$	0	$\dfrac{\pi}{6}$	$\dfrac{\pi}{3}$	$\dfrac{\pi}{2}$	$\dfrac{2\pi}{3}$	$\dfrac{5\pi}{6}$	$\pi$
$r$

c Sketch the graph by hand on the grid below.

Answer

Sketching Familiar Equations

You should also be able to sketch the standard polar graphs by hand. Once you recognize an equation as a particular type of graph, say a rose or a limaçon, you can sketch the graph quickly by finding just a few well-chosen guidepoints. The next example demonstrates a technique for sketching a rose.

Example 10.23

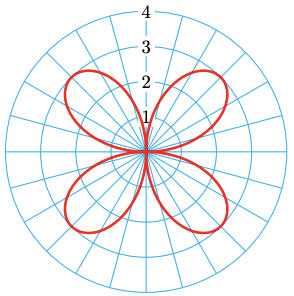
Graph the polar equation $r=3 \sin 2 \theta$.

Answer

Referring to the Catalog of Polar Graphs, we see that the graph of this equation is a rose, with petal length $a=3$ and four petals, because $2 n=4$. If we can locate the tips of the petals, we can use them as guidepoints to sketch the graph.

Now, the points at the tips of the petals have $r=3$, so we substitute $r=3$ into the equation of the rose to find the values of $\theta$ at those points.

$$\begin{aligned} 3 & =3 \sin 2 \theta \quad \quad &&\text{Divide both sides by 3.} \\ 1 & =\sin 2 \theta \quad \quad &&\text{Apply the arcsine function to both sides.}\\ \dfrac{\pi}{2} & =2 \theta \quad \quad &&\text{Divide both sides by 2.}\\ \dfrac{\pi}{4} & =\theta \end{aligned}$$

Thus, one of the petal tips is located at $\theta=\frac{\pi}{4}$. Because the 4 petals are evenly spaced around the pole, the angle between the petals is $\frac{2 \pi}{4}=\frac{\pi}{2}$, and the other petal tips occur at

$$\begin{aligned} \theta & =\dfrac{\pi}{4}+\dfrac{\pi}{2}=\dfrac{3 \pi}{4} \\ \theta & =\dfrac{\pi}{4}+2\left(\dfrac{\pi}{2}\right)=\dfrac{5 \pi}{4} \\ \theta & =\dfrac{\pi}{4}+3\left(\dfrac{\pi}{2}\right)=\dfrac{7 \pi}{4} \end{aligned}$$

We plot the tips of the petals as guidepoints, at $\left(3, \frac{\pi}{4}\right), \quad\left(3, \frac{3 \pi}{4}\right), \quad\left(3, \frac{5 \pi}{4}\right)$ and $\left(3, \frac{7 \pi}{4}\right)$. Now we can sketch a rose with 4 petals of length 3, as shown below.

Checkpoint 10.24

Graph the polar equation $r=4 \cos 5 \theta$.

Answer

The limaçons, $r=a \pm \sin \theta$ and $r=a \pm \cos \theta$, are another family of polar graphs. In particular, the cardioid is a special case of a limaçon with $a=b$.

Example 10.25

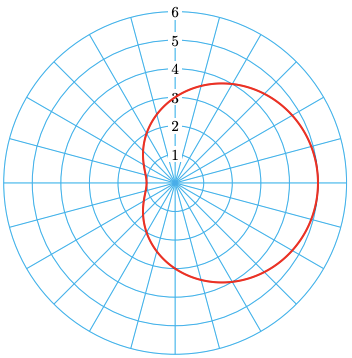
Graph the polar equation $r=3+2 \cos \theta$.

Answer

This is the equation for a limaçon, with $a=3$ and $b=2$. Because $a>b$, the limaçon will have a dent, like a lima bean, rather than a loop. As guide points, we locate the points at the four quadrantal angles.

$\theta$	$r = 3 + 2 \cos \theta$
0	5
$\dfrac{\pi}{2}$	3
$\pi$	1
$\dfrac{3\pi}{2}$	3

We plot the guide points and connect them in order with a smooth curve, as shown below. Note that this limaçon involving cosine is symmetric about the $x$-axis; limaçons involving sine are symmetric about the $y$-axis.

Checkpoint 10.26

Graph the polar equation $r=1-3 \sin \theta$.

Answer

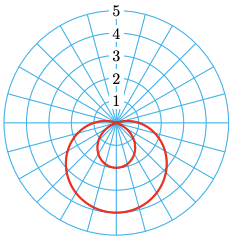
You should also be able to identify a polar graph and write its equation.

Example 10.27

Give a polar equation for each of the graphs below.

Answer

a The graph is a circle centered at (-2,0) and with radius 2, so we choose the equation $r=2 a \cos \theta$, with $a=-2$. Thus, $r=-4 \cos \theta$.

b The graph is a cardioid with its axis of symmetry on the $x$-axis, and the "bottom" of the heart points in the positive $x$ direction, so its equation has the form $r=a+a \cos \theta$. At $\theta=0, r=2$, so we can solve for $a$:

$2=a+a \cos 0$

$2=a+a(1)=2 a$

Thus, $a=1$ and we choose the equation $r=1+\cos \theta$.

Checkpoint 10.28

Give a polar equation for each of the graphs below.

Answer

a $r^2=4 \sin 2 \theta$

b $r=1-\sin \theta$

Finding Intersection Points

To find the intersection points of two graphs, we solve the system made up of their equations. If the equations are $y=f(x)$ and $y=g(x)$, we simply solve the equation $f(x)=g(x)$. For example, we find the intersection points of $y=x^2$ and $y=x+2$ by solving the equation $x^2-x-2=0$ to get

$$\begin{aligned} x^2-x-2 & =0 \\ (x-2)(x+1) & =0 \\ x-2=0, \quad x+1 & =0 \\ x=2, \quad x & =-1 \end{aligned}$$

These are the $x$-coordinates of the intersection points, and we can find the $y$-coordinates by substituting these values into either equation.

• For $x=2$, we find $y=2^2=4$.
• For $x=-1$, we find $y=(-1)^2=1$.

Thus, the intersection points are (2, 4) and (−1, 1), as shown below.

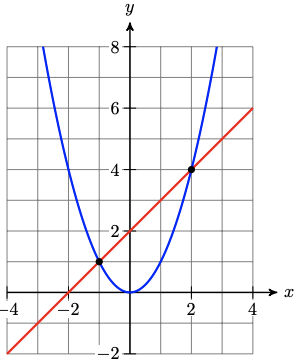
To find the intersection points of the polar graphs $r=f(\theta)$ and $r=g(\theta)$ we solve the equation $f(\theta)=g(\theta)$.

Example 10.29

Find all intersection points of the graphs of $r=2+2 \sin \theta$ and $r=2+2 \cos \theta$.

Answer

We equate the two expressions for $r$ and solve for $\theta$.

$$\begin{aligned} r=2+2 \sin \theta & =r=2+2 \cos \theta \\ \sin \theta & =\cos \theta \quad \quad &&\text{Divide both sides by }\cos \theta.\\ \tan \theta & =1 \quad \quad &&\text{Solve for }\theta. \\ \theta &= \dfrac{\pi}{4}, \dfrac{5\pi}{4} \end{aligned}$$

We evaluate either expression for $t$ to find the other coordinate of the intersection point.

when $\quad \theta=\dfrac{\pi}{4}, \quad r=2+2 \sin \dfrac{\pi}{4}=2+\left(\dfrac{1}{\sqrt{2}}\right)=2+\sqrt{2}$

when $\quad \theta=\dfrac{5 \pi}{4}, \quad r=2+2 \sin \dfrac{5 \pi}{4}=2+\left(\dfrac{-1}{\sqrt{2}}\right)=2-\sqrt{2}$

Thus, two of the intersection points are $\left(2+\sqrt{2}, \frac{\pi}{4}\right)$ and $\left(2-\sqrt{2}, \frac{5 \pi}{4}\right)$, as shown below. However, you can see in the figure that the graphs also appear to intersect at the pole. To verify that the pole indeed lies on both graphs, we can solve for $\theta$ in each equation when $r=0$.

However, you can see in the figure that the graphs also appear to intersect at the pole. To verify that the pole indeed lies on both graphs, we can solve for $\theta$ in each equation when $r=\mathbf{0}$.

$$\begin{aligned} 0 & =2+2 \sin \theta & 0 & =2+2 \cos \theta \\ -1 & =\sin \theta & -1 & =\cos \theta \\ \theta & =\dfrac{3 \pi}{2} & \theta & =\pi \end{aligned}$$

Both points, $\left(0, \frac{3 \pi}{2}\right)$ and $(0, \pi)$, represent the pole. Thus, the graphs intersect at three points: $\left(2+\sqrt{2}, \frac{\pi}{4}\right),\left(2-\sqrt{2}, \frac{5 \pi}{4}\right)$, and the pole.

Caution 10.30

As we saw in the previous Example, solving a system of equations $r=f(\theta)$ and $r=g(\theta)$ will not always reveal an intersection at the pole, because $r$ may be equal to zero for different values of $\theta$ in the two equations. We should always check separately whether the pole is a point on both graphs.

Checkpoint 10.31

Find all intersection points of the graphs of $r=1$ and $r=2 \cos \theta$.

Answer

$\left(1, \dfrac{\pi}{3}\right),\left(1, \dfrac{5 \pi}{3}\right)$

Review the following skills you will need for this section.

Skills Refresher 10.2

Solve each equation. Give two solutions, $0 \leq \theta \leq 2 \pi$.

1 $\cos \theta = \dfrac{\sqrt{3}}{2}$

2 $\sin \theta = \dfrac{1}{\sqrt{2}}$

3 $\tan \theta = \sqrt{3}$

4 $\tan \theta = \dfrac{1}{\sqrt{3}}$

5 $\sin \theta = \dfrac{11}{\sqrt{2}}$

6 $\cos \theta = \dfrac{-1}{2}$

7 $\tan \theta = -1$

8 $\cos \theta = 0$

Skills Refresher Answers

1 $\dfrac{\pi}{6}, \dfrac{11\pi}{6}$

2 $\dfrac{\pi}{4}, \dfrac{3\pi}{4}$

3 $\dfrac{\pi}{3}, \dfrac{4\pi}{3}$

4 $\dfrac{\pi}{6}, \dfrac{7\pi}{6}$

5 $\dfrac{5\pi}{4}, \dfrac{7\pi}{4}$

6 $\dfrac{2\pi}{3}, \dfrac{4\pi}{3}$

7 $\dfrac{3\pi}{4}, \dfrac{7\pi}{4}$

8 $\dfrac{\pi}{2}, \dfrac{3\pi}{2}$

A Catalog of Polar Curves

The Coordinate Curves

• $\theta = k$ ($k$ a constant)
  A line through the pole.
  $k$ gives the angle of inclination of the line (in radians).
  
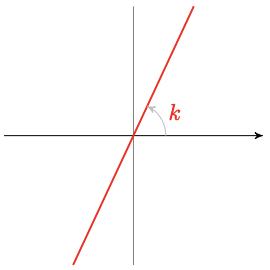
• $r = k$ ($k$ a constant)
  A circle centered at the pole.
  $k$ is the radius of the circle.
  

Circles

• $r = 2a \sin \theta$
  A circle with center (0, $a$) on the $y$-axis, and radius $|a|$.
  
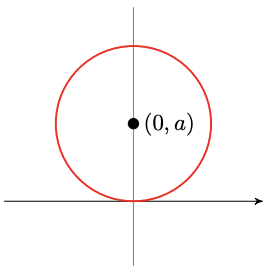
• $r = 2a \cos \theta$
  A circle with center $(a,0)$ on the $x$-axis, and radius $|a|$.
  

Roses

• $r = a \sin n\theta$
  A rose with petal length $a$.
  $n$ petals if $n$ is odd; $2n$ petals if $n$ is even.
  
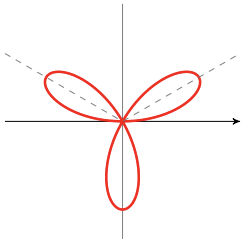
• $r = a \cos n \theta$
  A rose with petal length $a$.
  $n$ petals if $n$ is odd; $2n$ petals if $n$ is even.
  

Limaçons

$r = a \pm b \sin \theta \quad \text{ or } r = a \pm b \cos \theta$

• $a > b$, with a dent.

• $a < b$, with a loop.

• $a > b$, a cardioid.

Lemniscates

• $r^2 = a^2 \cos 2\theta$

• $r^2 = a^2 \sin 2\theta$

Spirals

• Archimedean spiral

$r^2 = a^2 \cos 2\theta$

• Logarithmic spiral

$r^2 = a^2 \sin 2\theta$

Section 10.2 Summary

Vocabulary

• Rose

• Limaçon

• Cardioid

• Lemniscate

Concepts

1 When graphing an equation in polar coordinates, we think of sweeping around the pole in the counterclockwise direction, and at each angle $\theta$ the $r$-value tells us how far the graph is from the pole.

2 Standard graphs in polar coordinates include circles and roses, cardioids and limaçons, lemniscates, and spirals.

3 To find the intersection points of the polar graphs $r=f(\theta)$ and $r=g(\theta)$ we solve the equation $f(\theta)=g(\theta)$. In addition, we should always check whether the pole is a point on both graphs.

Study Questions

1 Delbert says that the graph of $r=2 \sin \theta$ in the first example cannot be correct, because there are no points on the graph for angles between $\pi$ and $2 \pi$. How do you respond?

2 Is it possible to have a rose with only two petals? What would its equation be?

3 Francine says that a circle of the form $r=2 a \cos \theta$ is just a special case of a limaçon. Support or refute her statement.

4 There are no points on the graph of $r^2=4 \cos 2 \theta$ for angles between $\frac{\pi}{4}$ and $\frac{3 \pi}{4}$ Why is that?

Skills

1 Describe the effect of parameters in polar curves #1–16, 83–84

2 Compare polar and Cartesian graphs #21–24

3 Sketch standard polar graphs #17–20, 25–42, 75–82

4 Identify standard polar graphs #43–58

5 Write equations for standard polar graphs #59–66

6 Find intersection points of polar graphs #67–74

Homework 10-2

In Problems 1-4, use your calculator to graph the equations.

1

a Graph $r=k$, for $k=1,2,3$. How does the graph change for different values of $k$?

b Write a Cartesian equation for each graph in part (a).

2

a Graph $r=k$, for $k=-1,-2,-3$. How does these graphs compare to the graphs in Problem 1?

b Write a Cartesian equation for each graph in part (a).

3

a Graph $\theta=k$, for $k=\dfrac{\pi}{6}, \dfrac{\pi}{3}, \dfrac{2 \pi}{3}, \dfrac{5 \pi}{6}$. How does the graph change for different values of $k$?

b Write a Cartesian equation for each graph in part (a).

4

a Graph $\theta=k$, for $k=\dfrac{7 \pi}{6}, \dfrac{5 \pi}{3}, \dfrac{7 \pi}{3}, \dfrac{11 \pi}{6}$. How does the graph change for different values of $k$?

b Write a Cartesian equation for each graph in part (a).

5. Complete the table of values for each equation. Plot the points in order of increasing $\theta$. What is different about the two graphs?

Equation 1: $r = 2$

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$
$r=2$

Equation 2: $r = −2$

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$
$r=-2$

6. Graph each line, and label the points with their coordinates. How are the points on the two lines related?

Equation 1: $\theta = \dfrac{\pi}{4}$

$\theta = \dfrac{\pi}{4}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{4}$	$\dfrac{\pi}{4}$
$r$	-2	-1	0	1	2

Equation 1: $\theta = \dfrac{5\pi}{4}$

$\theta = \dfrac{5\pi}{4}$	$\dfrac{5\pi}{4}$	$\dfrac{5\pi}{4}$	$\dfrac{5\pi}{4}$	$\dfrac{5\pi}{4}$	$\dfrac{5\pi}{4}$
$r$	-2	-1	0	1	2

7.

a Graph the circle $r = 4 \cos \theta$. Label the points corresponding to $\theta = 0, \dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3\pi}{4}$, and $\pi$.

b Complete the table of values. What happens to the graph as $\theta$ increases from $\pi$ to $2\pi$?

$\theta$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

c Find the center and radius of the circle.

d Give the Cartesian equation of the circle.

8.

a Graph the circle $r = 4 \sin \theta$. Label the points corresponding to $\theta = 0, \dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3\pi}{4}$, and $\pi$.

b Complete the table of values. What happens to the graph as $\theta$ increases from $\pi$ to $2\pi$?

$\theta$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

c Find the center and radius of the circle.

d Give the Cartesian equation of the circle.

9.

a Graph $r=2 a \sin \theta$ for $a=-2,-1,1,2$.

b How do the graphs change for different values of $a$?

10.

a Graph $r=2 a \cos \theta$ for $a=-2,-1,1,2$.

b How do the graphs change for different values of $a$?

11. Complete the table of values for each cardioid, and graph the equation.

$\theta$	0	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$
$r$

a $r=1+\sin \theta$

b $r=-1+\sin \theta$

c $r=1-\sin \theta$

d $r=-1-\sin \theta$

12. Complete the table of values for each cardioid, and graph the equation.

$\theta$	0	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$
$r$

a $r=1+\cos \theta$

b $r=-1+\cos \theta$

c $r=1-\cos \theta$

d $r=-1-\cos \theta$

13. Complete the table of values for each limaçon, and graph the equation.

$\theta$	0	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$
$r$

a $r=2+\cos \theta$

b $r=2-\cos \theta$

c $r=1+2 \cos \theta$

d $r=1-2 \cos \theta$

14. Complete the table of values for each limaçon, and graph the equation.

$\theta$	0	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{3\pi}{2}$	$2\pi$
$r$

a $r=2+\sin \theta$

b $r=2-\sin \theta$

c $r=1+2 \sin \theta$

d $r=1-2 \sin \theta$

15.

a Graph the following roses and compare. How is the number of petals related to the value of $n$ in the equation $r=a \sin n \theta$?

$r=\sin 2 \theta, \quad r=\sin 3 \theta, \quad r=\sin 4 \theta, \quad r=\sin 5 \theta$

b For each graph above, list the values of $\theta$ where the tips of the petals occur.

c Graph $r=a \sin 3 \theta$ for $a=1,2$, and 3. How does the value of $a$ affect the graph?

16.

a Graph the following roses and compare. How is the number of petals related to the value of $n$ in the equation $r=a \cos n \theta$?

$r=\cos 2 \theta, \quad r=\cos 3 \theta, \quad r=\cos 4 \theta, \quad r=\cos 5 \theta$

b For each graph above, list the values of $\theta$ where the tips of the petals occur.

c Graph $r=a \cos 3 \theta$ for $a=1,2$, and 3 . How does the value of $a$ affect the graph?

17.

a Solve $r^2=9 \cos 2 \theta$ for $r$. (You should get two equations for $r$.)

b Graph both equations together. Change $\theta$ step to 0.02 to see the whole graph.

c How does the value of $a$ affect the graph of $r^2=a^2 \cos 2 \theta$?

18.

a Solve $r^2=9 \cos 2 \theta$ for $r$. (You should get two equations for $r$.)

b Graph both equations together. Change $\theta$ step to 0.02 to see the whole graph.

c How does this graph differ from the graph in Problem 17?

19. Graph the Archimedean spiral $r=\theta$. Set your window to

$$\begin{aligned} & \theta \min =0 \quad \quad \quad &&\theta \max =8 \pi \\ & \mathrm{Xmin}=-20 \quad \quad &&\mathrm{X} \max =20 \\ & \mathrm{Y} \min =-20 \quad \quad &&\mathrm{Y} \max =20 \\ \end{aligned}$$

Then graph by pressing Zoom 5.

20. Graph the logarithmic spiral $r=e^{0.2 \theta}$. Set your window to

$$\begin{aligned} & \theta \min =0 \quad &&\theta \max =8 \pi \\ & \mathrm{Xmin}=-100 \quad &&\mathrm{X} \max =100 \\ & \mathrm{Ymin}=-100 \quad &&\mathrm{Y} \max =100 \\ \end{aligned}$$

Then graph by pressing Zoom 5.

21.

a Complete the table and graph the equation $y=\sin 3 \theta$ in Cartesian coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$
$3\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$

b Complete the table and graph the equation $r = \sin 3 \theta$ in polar coordinates, for $0 \leq \theta \leq 2\pi$.

$\theta$
$3\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

22.

a Complete the table and graph the equation $y=\cos 2 \theta$ in Cartesian coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$
$2\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	\(\dfrac{3\pi}{4}\0	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$

b Complete the table and graph the equation $r=\cos 2 \theta$ in polar coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$
$2\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

23.

a Complete the table and graph the equation $y=2+2 \cos \theta$ in Cartesian coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$

b Complete the table and graph the equation $r=2+2 \cos \theta$ in polar coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

24.

a Complete the table and graph the equation $y=1-\sin \theta$ in Cartesian coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$y$

b Complete the table and graph the equation $r=1-\sin \theta$ in polar coordinates, for $0 \leq \theta \leq 2 \pi$.

$\theta$	0	$\dfrac{\pi}{4}$	$\dfrac{\pi}{2}$	$\dfrac{3\pi}{4}$	$\pi$	$\dfrac{5\pi}{4}$	$\dfrac{3\pi}{2}$	$\dfrac{7\pi}{4}$	$2\pi$
$r$

For Problems 25-42, use the catalog of polar graphs to help you identify and sketch the following curves. Check your work by graphing with a calculator.

25. $r=3 \cos \theta$

26. $r=2 \sin \theta$

27. $\theta=\dfrac{\pi}{4}$

28. $\theta=\dfrac{4 \pi}{3}$

29. $r=4$

30. $r=2$

31. $r=2+2 \sin \theta$

32. $r=3+3 \cos \theta$

33. $r=2-\cos \theta$

34. $r=1-3 \sin \theta$

35. $r=3 \sin 2 \theta$

36. $r=2 \cos 3 \theta$

37. $r=2 \cos 5 \theta$

38. $r=4 \sin 4 \theta$

39. $r=2+3 \sin \theta$

40. $r=3+2 \sin \theta$

41. $r^2=\cos 2 \theta$

42. $r^2=4 \sin 2 \theta$

For Problems 43–52, identify each curve, and graph it.

43. $r \csc \theta=2$

44. $r=2 \sec \theta$

45. $r^2=4,0 \leq \theta \leq \dfrac{3 \pi}{4}$

46. $\theta=\dfrac{\pi}{4},|r|<2$

47. $r=\sin \theta, \dfrac{3 \pi}{4} \leq \theta \leq \dfrac{5 \pi}{4}$

48. $r=\cos \theta, 0 \leq \theta \leq \dfrac{\pi}{2}$

49. $r=2 \sin 2 \theta \cos 2 \theta$

50. $r=\cos ^2 \theta-\sin ^2 \theta$

51. $r(1-\cos \theta)=\sin ^2 \theta$

52. $r \sec \theta=\sec \theta-\tan \theta$

For Problems 53–58, graph the following polar curves. Do you recognize them?

53. $r=\dfrac{2}{1-\cos \theta}$

54. $r=\dfrac{6}{2+\sin \theta}$

55. $r=\dfrac{2}{2-\cos \theta}$

56. $r=\dfrac{1}{1+\sin \theta}$

57. $r=\dfrac{1}{1+2 \sin \theta}$

58. $r=\dfrac{3}{2-3 \cos \theta}$

For Problems 59–66, write a polar equation for the graph.

59.

60.

61.

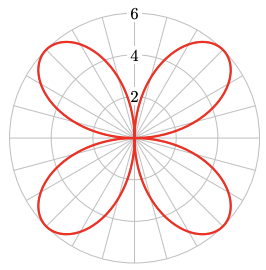
62.

63.

64.

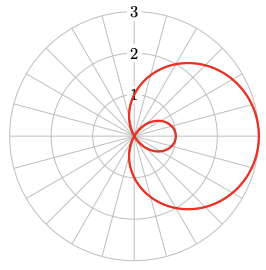
65.

66.

For Problems 67–74, find the coordinates of the intersection points of the two curves analytically. Then graph the curves to verify your answers.

67. $r=\cos \theta, r=1-\cos \theta$

68. $r=\sin \theta, r=\cos \theta$

69. $r=3 \sin \theta, r=3 \cos \theta$

70. $r=\sin 2 \theta, r=\cos 2 \theta$

71. $r=1, r=1-\cos \theta$

72. $r=3 \cos \theta, r=1+\cos \theta$

73. $r=2+\sin \theta, r=2-\cos \theta$

74. $r=\sin \theta, r=\sin 2 \theta$

For Problems 75–82, graph the polar curve.

75. $r^2=\tan \theta$

76. $r^2=\cot \theta$

77. $r=\csc \theta-2$ (conchoid)

78. $r=\tan \theta$ (kappa curve)

79. $r=\cos 2 \theta \sec \theta$ (strophoid)

80. $r=\sin \theta \tan \theta$ (cissoid)

81. $r=\dfrac{1}{\sqrt{\theta}}$

82. $r=\cos \dfrac{\theta}{2}, 0 \leq \theta \leq 4 \pi$

83. Graph the polar curves $r=1-2 \sin n \theta$ for $n=2,3,4,5,6$. Explain how the value of the parameter $n$ affects the curve.

84. Graph the polar curves $r=1-3 \cos n \theta$ for $n=2,3,4,5,6$. Explain how the value of the parameter $n$ affects the curve.