13.4: Modeling Spatial Movement
- Page ID
- 7846
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now we will discuss how to write a PDE-based mathematical model for a dynamical process that involves spatial movement of some stuff. There are many approaches to writing PDEs, but here in this textbook, we will use only one “template,” called the transport equation. Here is the equation:
\[\dfrac{\partial{c}}{\partial{t}} = -{∇}·{J} + s \label{13.14} \]
Here, \(c\) is the system’s state defined as a spatio-temporal function that represents the concentration of the stuff moving in the space. \({J}\) is a vector field called the flux of \(c\). The magnitude of the vector \(J\) at a particular location represents the number of particles moving through a cross-section of the space per area per unit of time at that location. Note that this is exactly the same as the vector field \(v\) we discussed when we tried to understand the meaning of divergence. Therefore, the first term of Equation \ref{13.14} is coming directly from Equation (13.2.11). The second term, \(s\), is often called a source/sink term, which is a scalar field that represents any increase or decrease of \(c\) taking place locally. This is often the result of influx or outflux of particles from/to the outside of the system. If the system is closed and the total amount of the stuff is conserved, you don’t need the source/sink term, and the transport equation becomes identical to Equation (13.2.11).
There is another way of writing a transport equation. While Equation \ref{13.14} explicitly describes the amount of particles’ movement per area per unit of time in the form of flux \(J\), another convenient way of describing the movement is to specify the velocity of the particles, and then assume that all the particles move at that velocity. Specifically:
\[\dfrac{\partial{c}}{\partial{t}} = −∇·(cw) + s \label{13.15} \]
Here, \(w\) is the vector field that represents the velocity of particles at each location. Since all the particles are moving at this velocity, the flux is given by \(J = cw.\) Which formulation you should use, Equation \ref{13.14} or Equation \ref{13.15}, depends on the nature of the system you are going to model.
As you can see above, the transport equation is very simple. But it is quite useful as a starting point when you want to describe various kinds of spatial phenomena. One example is to derive a diffusion equation. How can you write a PDE-based model of diffusion dynamics by which the spatial distribution of things tends to smoothen over time (Figure \(\PageIndex{1}\))?
To develop a model of diffusion using the transport equation, we need to think about the direction of the movement in this process. In diffusion, particles tend to move randomly at microscopic scales, but macroscopically, they tend to “flow” from high to low, bringing down the humps while filling up the dips (Figure \(\PageIndex{1}\), left), eventually resulting in a completely leveled surface. Therefore, a natural choice of the direction of particles’ movement is the opposite of the gradient of the distribution of the particles (\(−α∇c\), where \(α\) is a positive constant).
The next question you may want to ask is: Which formula should you use, Equation \ref{13.14} or Equation \ref{13.15}? To make a decision, you should think about whether\(−α∇c\) only gives the velocity of movement or it also determines the actual magnitude of the flux. If the former is the case, all the particles at the same location will move toward that direction, so the actual flux should be given by \(−c(α∇c)\). But this means that the speed of diffusion will be faster if the whole system is “elevated” by adding 10 to \(c\) everywhere. In other words, the speed of diffusion will depend on the elevation of the terrain! This doesn’t sound quite right, because the diffusion is a smoothing process of the surface, which should depend only on the shape of the surface and should not be affected by how high or low the overall surface is elevated. Therefore, in this case, Equation \ref{13.14} is the right choice; we should consider \(−α∇c\) the actual flux caused by the diffusion. This assumption is called Fick’s first law of diffusion, as it was proposed by Adolf Fick in the 19th century.
Plugging \(J = −α∇c \)into Equation \ref{13.14}, we obtain
\[\begin{align} \dfrac{\partial{c}}{\partial{t}} &= −∇·(−α∇c) + s \\[4pt] &= ∇·(α∇c) + s. \label{(13.16)} \end{align} \]
If \(α\) is a homogeneous constant that doesn’t depend on spatial locations, then we can take it out of the parentheses:
\[\dfrac{\partial{c}}{\partial{t}}=α∇^{2}c + s \label{(13.17)} \]
Now we see the Laplacian coming out! This is called the diffusion equation, one of the most fundamental PDEs that has been applied to many spatio-temporal dynamics in physics, biology, ecology, engineering, social science, marketing science, and many other disciplines. This equation is also called the heat equation or Fick’s second law of diffusion. \(α\) is called the diffusion constant, which determines how fast the diffusion takes place.
We could still consider an alternative smoothing model in which the flux is given by \(−c(α∇c)\), which makes the following model equation:
\[\dfrac{\partial{c}}{\partial{t}} =α∇·(c∇c) + s \label{(13.18)} \]
Explain what kind of behavior this equation is modeling. Discuss the difference between this model and the diffusion equation (Equation \ref{(13.17)}).
Develop a PDE model that describes a circular motion of particles around a certain point in space.
Develop a PDE model that describes the attraction of particles to each other.
We can develop more complex continuous field models by combining spatial movement and local dynamics together, and also by including more than one state variable. Let’s try developing a PDE-based model of interactions between two state variables: population distribution (\(p\) for “people”) and economic activity (\(m\) for “money”). Their local (non-spatial) dynamics are assumed as follows:
1. The population will never increase or decrease within the time scale being considered in this model.
2. The economy is activated by having more people in a region.
3. The economy diminishes without people.
In the meantime, their spatial dynamics (movements) are assumed as follows:
4. Both the population and the economic activity diffuse gradually.
5. People are attracted to the regions where economy is more active.
Our job is to translate these assumptions into mathematical equations by filling in the boxes below.
\(\dfrac{\partial{p}}{\partial{t}} = \Box \)
\(\dfrac{\partial{m}}{\partial{t}} = \Box \)
First, give it a try by yourself! Then go on to the following.
Were you able to develop your own model? Let’s go over all the assumptions to see how we can write each of them in mathematical form.
Assumption 1 says there is no change in the population by default. So, this can be written simply as
\[\dfrac{\partial{m}}{\partial{t}} =\alpha{p}, \label{(13.19)} \]
where \(α\) is a positive constant that determines the rate of production of the economy per capita.
Assumption 3 tells that the economy should naturally decay if there is no influence from people. The simplest model of such decay would be that of exponential decay, which can be represented by including a linear term of \(m\) with a negative coefficient in the equation for \(m\), so that:
\[\dfrac{\partial{m}}{\partial{t}} =\alpha{p} -\beta {m}. \label{(13.21)} \]
Again, \(β\) is a positive constant that determines the decay rate of the economy. This equation correctly shows exponential decay if \(p = 0\), which agrees with the assumption. So far, all the assumptions implemented are about local, non-spatial dynamics. Therefore we didn’t see any spatial derivatives.
Now, Assumption 4 says we should let people and money diffuse over space. This is about spatial movement. It can be modeled using the diffusion equation we discussed above (Equation \ref{(13.17)}). There is no need to add source/sink terms, so we just add Laplacian terms to both equations:
\[\dfrac{\partial{p}}{\partial{t}} = D_{p}∇^{2}p \label{(13.22)} \]
\[\dfrac{\partial{m}}{\partial{t}} =D_{m}∇^{2}m +\alpha{p} -\beta{m} \label{(13.23)} \]
Here, \(D_p\) and \(D_m\) are the positive diffusion constants of people and money, respectively.
Finally, Assumption 5 says people can sense the “smell” of money and move toward areas where there is more money. This is where we can use the transport equation. In this case, we can use Equation \ref{13.15}, because all the people at a certain location would be sensing the same “smell” and thus be moving toward the same direction on average. We can represent this movement in the following transport term
\[−∇·(p γ∇m), \label{(13.24)} \]
where the gradient of \(m\) is used to obtain the average velocity of people’s movement (with yet another positive constant \(γ\)). Adding this term to the equation for \(p\) representspeople’s movement toward money.
So, the completed model equations look like this:
\[\dfrac{\partial{p}}{\partial{t}} =D_{p} \nabla^{2}p -\gamma \nabla \cdot(p\nabla{m}) \label{(13.25)} \]
\[\dfrac{\partial{m}}{\partial{t}} =D_{m} \nabla^{2}m +\alpha{m} -\beta{m} \label{(13.26)} \]
How does this model compare to yours?
Interestingly, a mathematical model that was essentially identical to our equations above was proposed nearly half a century ago by two physicists/applied mathematicians, Evelyn Keller and Lee Segel, to describe a completely different biological phenomenon [48, 49]. The Keller-Segel model was developed to describe chemotaxis—movement of organisms toward (or away from) certain chemical signals—of a cellular slime mold species Dictyostelium discoideum. These slime mold cells normally behave as individual amoebae and feed on bacteria, but when the food supply becomes low, they first spread over the space and then aggregate to form “slugs” for long-distance migration (Figure \(\PageIndex{2}\)). Keller and Segel developed a mathematical model of this aggregation process, where chemotaxis plays a critical role in cellular self-organization.
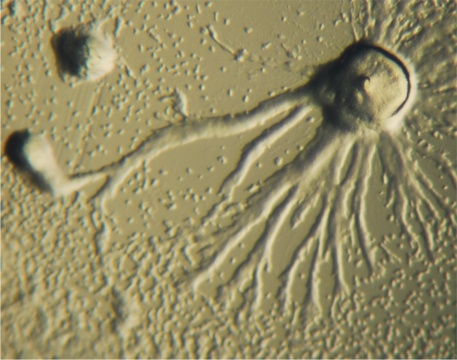
Keller and Segel made the following assumptions based on what was already known about these interesting cellular organisms:
- Cells are initially distributed over a space more or less homogeneously (with some random fluctuations).
- Cells show chemotaxis toward a chemical signal called cAMP (cyclic adenosine monophosphate).
- Cells produce cAMP molecules.
- Both cells and cAMP molecules diffuse over the space.
- Cells neither die nor divide.
Did you notice the similarity between these assumptions and those we used for the population-economy model? Indeed, they are identical, ifyoureplace“cells”with“people” and “cAMP” with “money.” We could use the word “moneytaxis” for people’s migration toward economically active areas!
The actual Keller-Segel equations look like this:
\[\dfrac{\partial{a}}{\partial{t}} =\mu\nabla^{2}\alpha -\chi \nabla \cdot (a\nabla{c}) \label{(13.27)} \]
\[\dfrac{\partial{c}}{\partial{t}} D \nabla^{2}c +fa-kc \label{(13.28)} \]
In fact, these equations are simplified ones given in [49], as the original equations were rather complicated with more biological details. \(a\) and \(c\) are the state variables for cell density and cAMP concentration, respectively. \(µ\) is the parameter for cell mobility, \(χ\) is the parameter for cellular chemotaxis, \(D\) is the diffusion constant of cAMP, \(f\) is the rate of cAMP secretion by the cells, and \(k\) is the rate of cAMP decay. Compare these equations with Eqs. \ref{(13.25)} and \ref{(13.26)}. They are the same! It is intriguing to see that completely different phenomena at vastly distant spatio-temporal scales could be modeled in an identical mathematical formulation.
It is known that, for certain parameter settings (which will be discussed in the next chapter), this model shows spontaneous pattern formation from almost homogeneous initial conditions A sample simulation result is shown in Fig. 13.4.3, where we see spots of aggregated cell clusters forming spontaneously. You will learn how to conduct simulations of continuous field models in the next section.
In Fig. 13.4.3, we can also observe that there is a characteristic distance between nearby spots, which is determined by model parameters (especially diffusion constants). The same observation applies to the formation of cities and towns at geographical scales. When you see a map, you will probably notice that there is a typical distance between major cities, which was probably determined by the human mobility centuries ago, among other factors.
Consider introducing to the Keller-Segel model a new variable b that represents the concentration of a toxic waste chemical. Make the following assumptions:
- cAMP gradually turns into the waste chemical (in addition to natural decay).
- The waste chemical diffuses over space.
- The waste chemical never decays naturally.

- Cells tend to avoid regions with high concentrations of the waste chemical.
- Revise the Keller-Segel equations to develop your new model.
Develop a PDE-based model that describes the dynamics of a predator-prey ecosystem with the following assumptions:
- The prey population grows following the logistic growth model.
- The predator population tends to decay naturally without prey.
- Predation (i.e., encounter of prey and predator populations) increases the predator population while it decreases the prey population.
- The predator population tends to move toward areas with high prey density.
- The prey population tends to move away from areas with high predator density.
- Both populations diffuse over space.


