Skip to main content
Mathematics LibreTexts

6.3: The M and J-sets similarity, Lei's theorem

  1. Last updated
  2. Save as PDF
  • Page ID
    102619

    • Robert L. Devaney
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Here Julia sets J(co) associated with the preperiodic points co near the point z = co are shown. These pictures are compared with the corresponding areas of the Mandelbrot set.

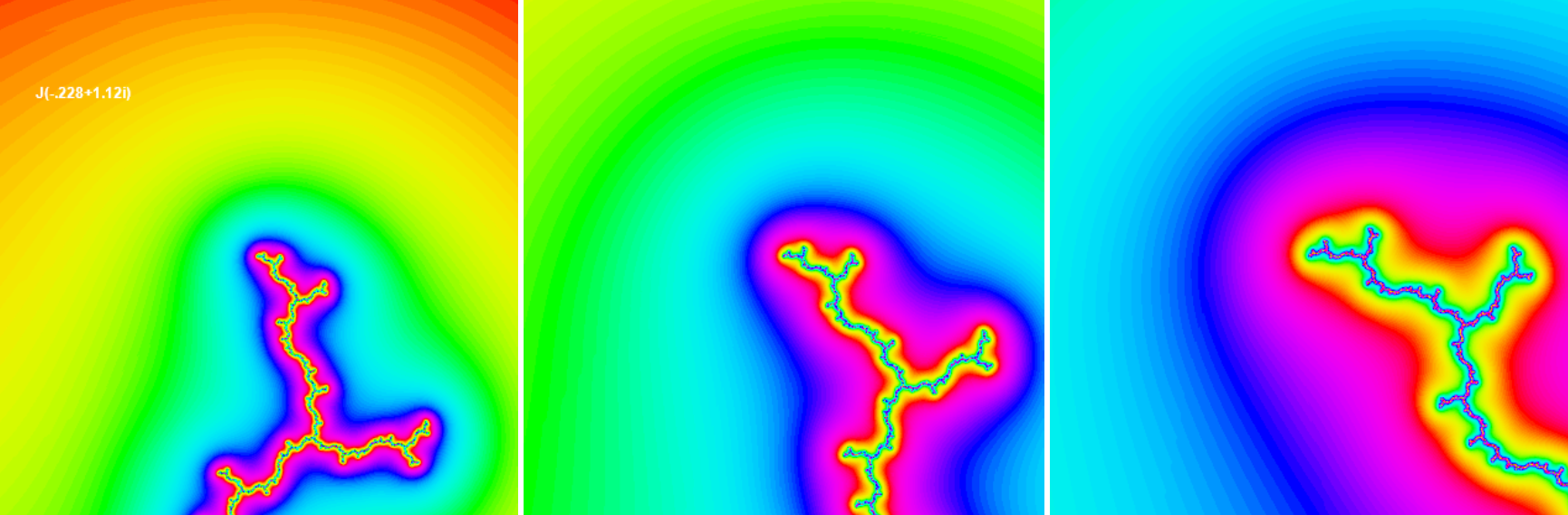
    6.3.1.png
    Figure \(\PageIndex{1}\)
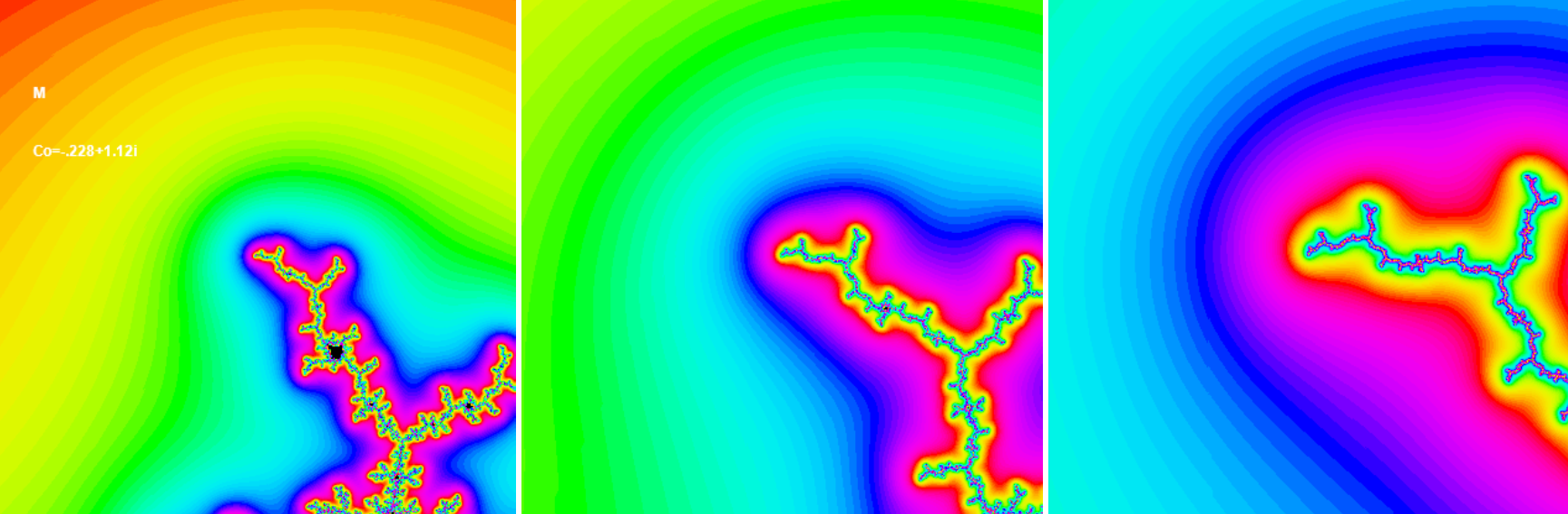
    6.3.2.png
    Figure \(\PageIndex{2}\)
    6.3.3.png
    Figure \(\PageIndex{3}\)
    6.3.4.png
    Figure \(\PageIndex{4}\)

    J pictures differ from the corresponding M pictures in that there are no black regions in them. On the other hand if we zoom in to a preperiodic point in M, the nearby miniature Ms shrink faster than the view window (if we shrink the picture by a factor of m the miniature Ms shrink by a factor of m2), so they eventually disappear.

    This local similarity between the Mandelbrot set near a preperiodic point co and the Julia set J(co ) near z = co shown above is the subject a theorem of Tan Lei.

    Here is a partial explanation for it in the case when period of co is 1. For small ε

        fCo+εo(n+1)(0) = fCo+εon(co + ε)
        = fCoon(co ) + ( d/dc fCon(0) |C=Co + d/dz fCoon(z) |z=Co ) ε + O(ε2)
        = fCoon(co + knε) + O(ε2)     ,

    where

        kn = ( d/dc fCon(co ) |C=Co + d/dz fCoon(z) |z=Co ) / d/dz fCoon(z) |z=Co .

    As since

        d/dc fCo(n+1)(co ) |C=Co = 2 hn d/dc fCon(co ) |C=Co + 1 ,
        d/dz fCoo(n+1)(z) |z=Co = 2 hn d/dz fCoon(z) |z=Co ,     hn = fCoon(co )

    and hn go to the fixed point h of the critical orbit of preperiodic point co for large enough n, then it can be shown, that kn converge to a finite k [Ravenel].

    Equation

        fCo+εo(n+1)(0) = fCoon(co + kε) + O(ε2)

    means that for small ε the (n+1)th point in critical orbit of c = co+ε can be approximated by the nth point in the Julia orbit of z∗ = co+kε . I.e. the critical orbit is bounded if and only if the z∗ orbit is bounded. This accounts for the local similarity between the Mandelbrot set near co and the Julia set J(co ) near z = co .

    This page titled 6.3: The M and J-sets similarity, Lei's theorem is shared under a Public Domain license and was authored, remixed, and/or curated by Robert L. Devaney via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.