Skip to main content
Mathematics LibreTexts

6.4: Embedded Julia midgets

  1. Last updated
  2. Save as PDF
  • Page ID
    102620

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    M and J-sets similarity. Embedded Julia midgets

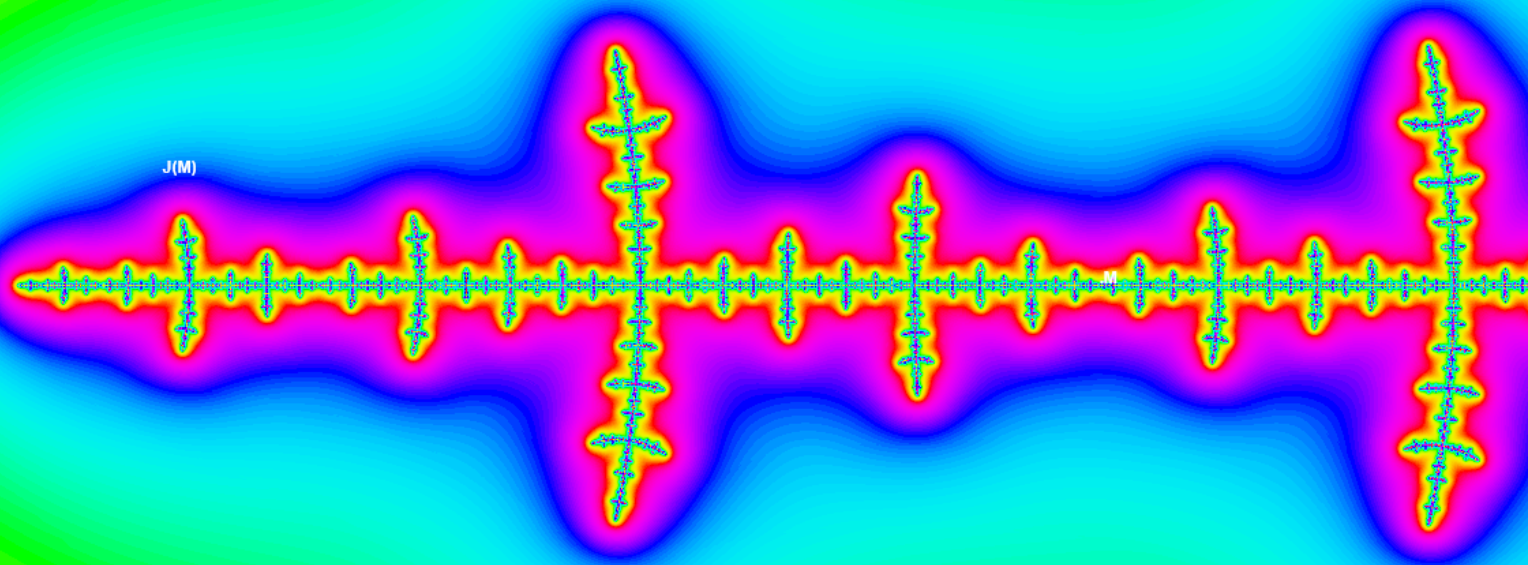
    Tan Lei's theorem says, that the M-set at a preperiodic point (e.g. at the band merging point M = -1.543689 in the second picture) and the Julia set J(M) at z = M are similar and have the same scaling constant.

    6.4.1.png
    Figure \(\PageIndex{1}\)
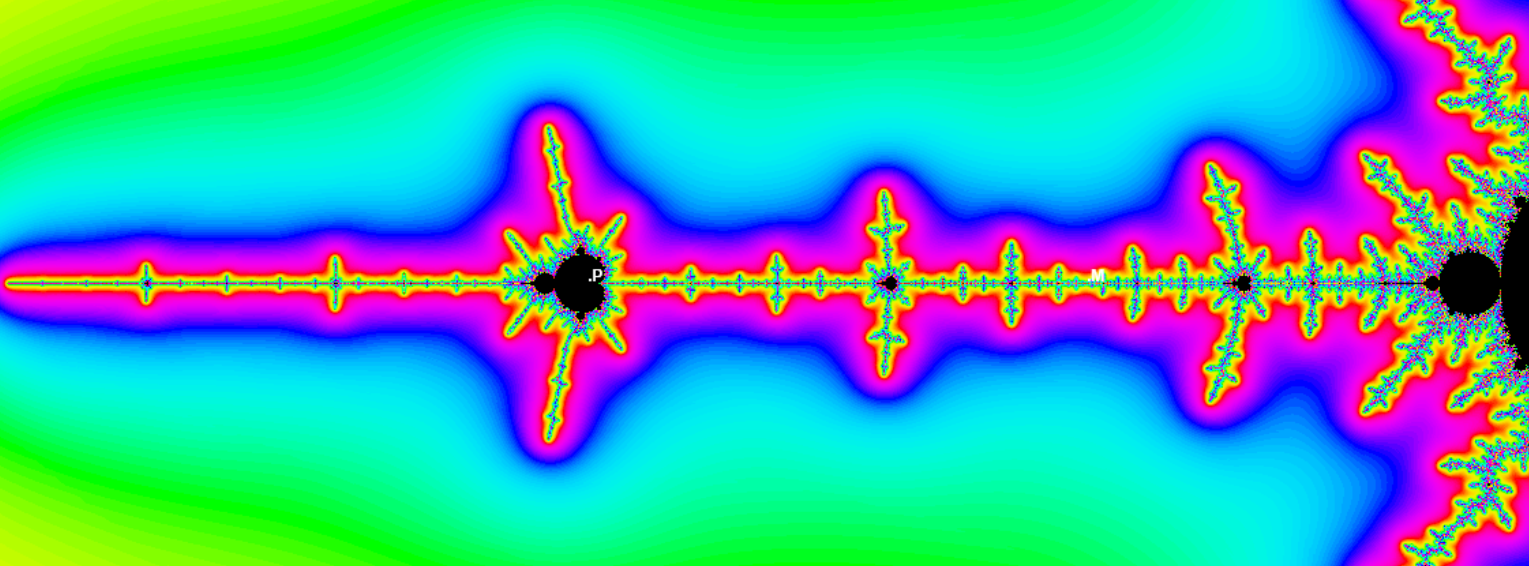
    6.4.2.png
    Figure \(\PageIndex{2}\)
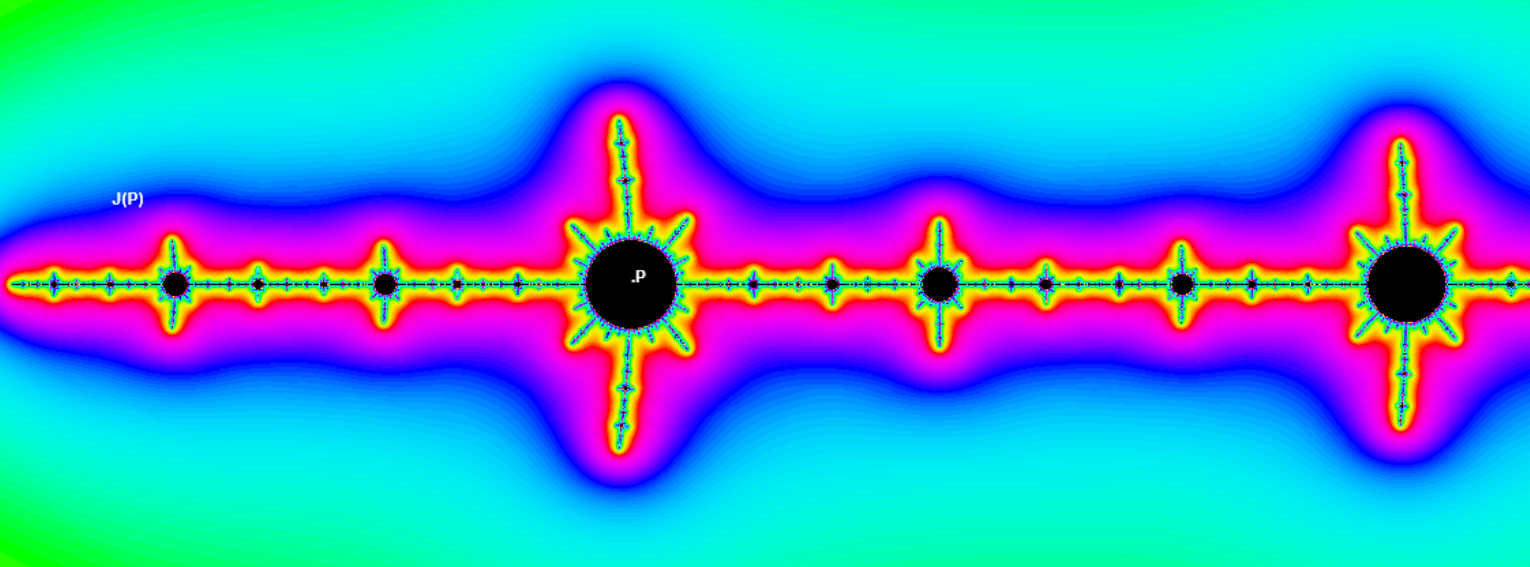
    6.4.3.png
    Figure \(\PageIndex{3}\)

    In the vicinity of the periodic point P = -1.75488 (in the center of the period-3 midget) the Mandelbrot set is similar again to the Julia set J(P). As since fco3 is renormalizable for c = P , we see the J(0) set at z = P and its shrinking copies (instead of sequence of tiny midgets in the M-set).

    At last this image corresponds to A = -1.7465234 at the cusp of the period-3 midget. The point A lays from outside of tiny cardioid, therefore we see small copies of the cauliflower Cantor dust J(0.35) set.

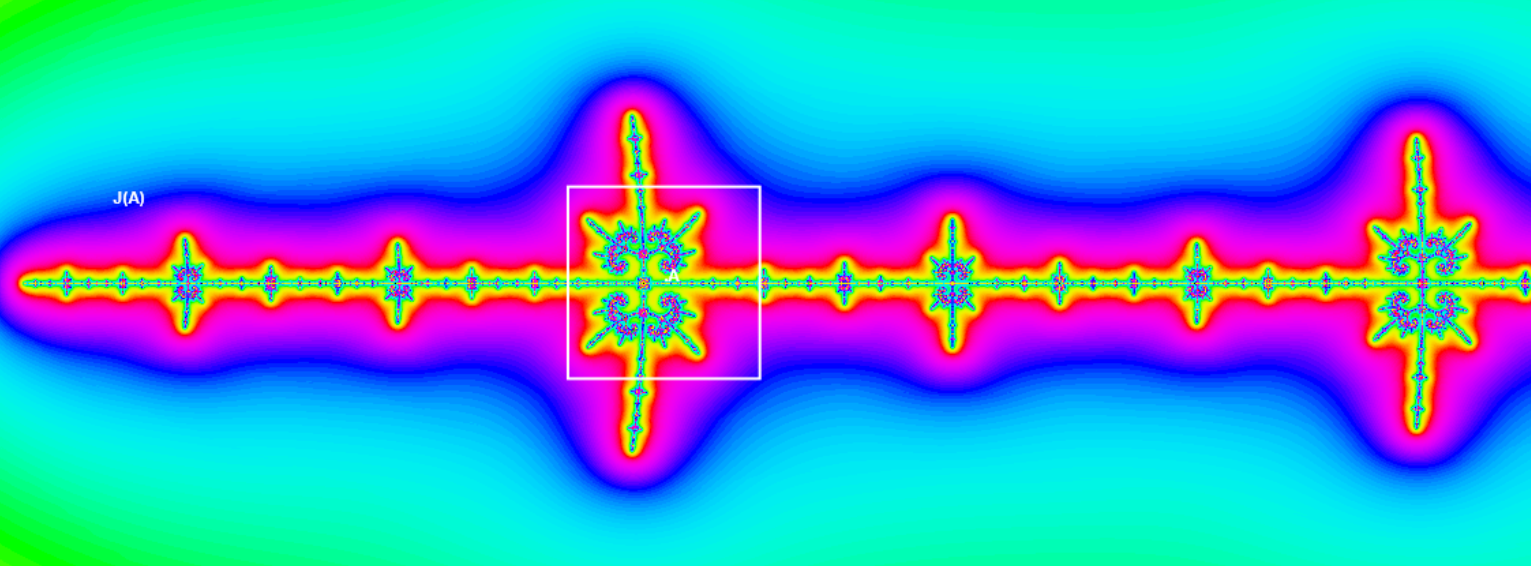
    6.4.4.png
    Figure \(\PageIndex{4}\)
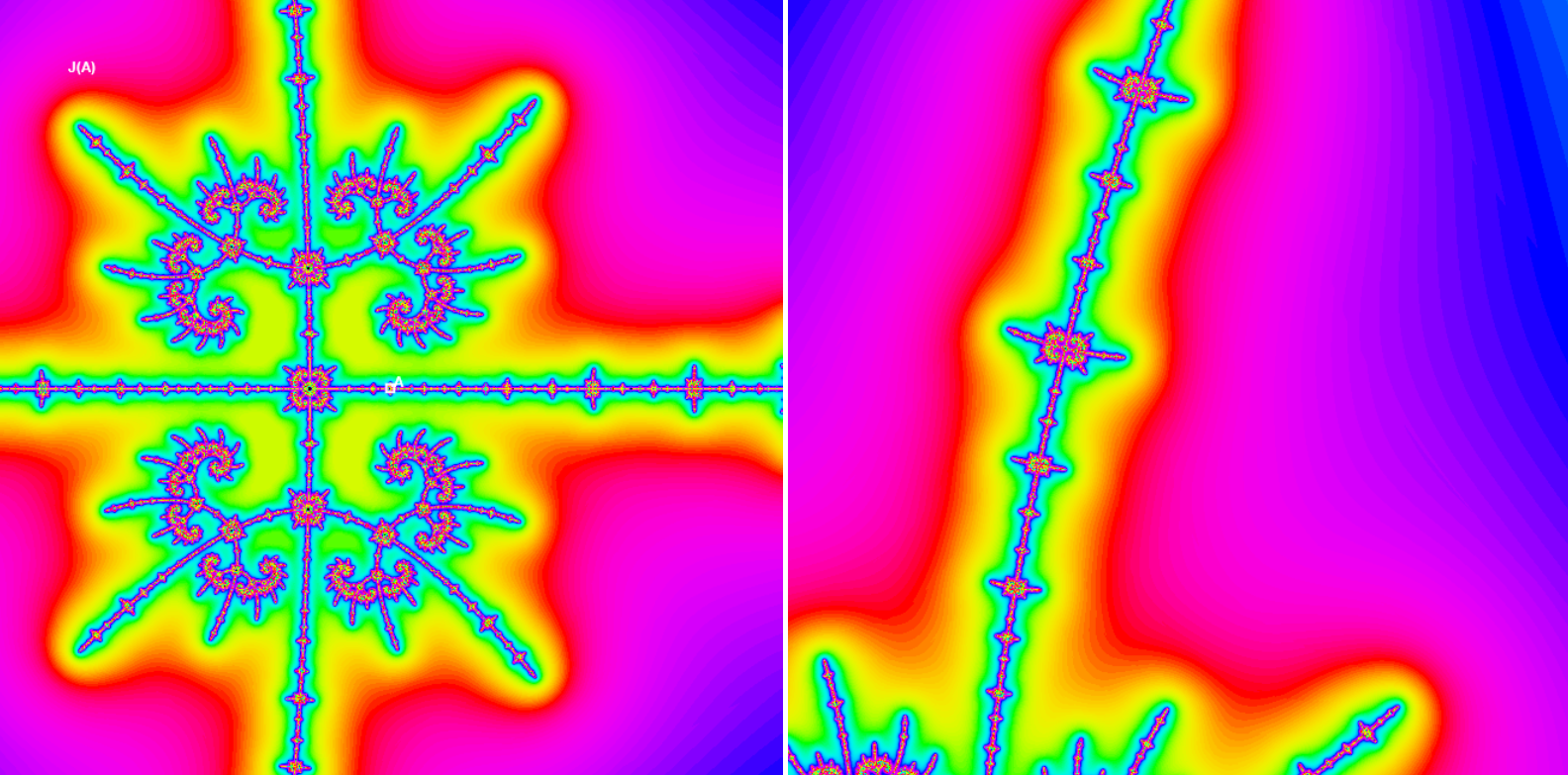
    6.4.5.jpg
    Figure \(\PageIndex{5}\)
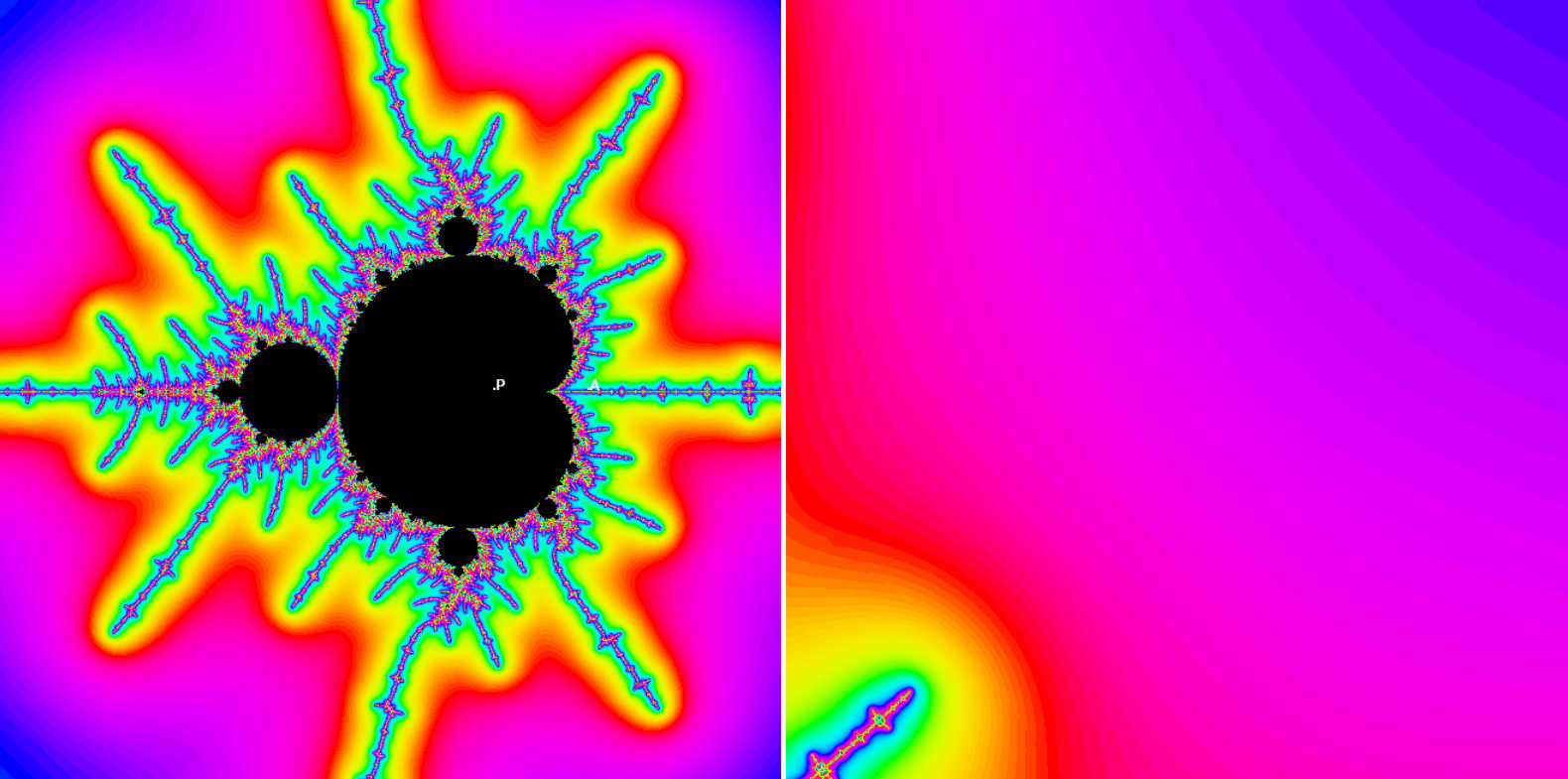
    6.4.6.jpg
    Figure \(\PageIndex{6}\)

    To make the last step we look at the M-set near A . As since at small scale the M-set is similar to corresponding J(A) set, we see embedded J(0.35) midget in the Mandelbrot set (in the right applet). Note however, that this "cauliflower" is replaced by the M-midget in the left window. Every embedded cauliflower has a tiny M-midget in its center.

    For more details see Robert P. Munafo's Embedded Julia Set.

     

    This page titled 6.4: Embedded Julia midgets is shared under a Public Domain license and was authored, remixed, and/or curated by via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.