1.3: Shifting and Reflecting

Last updated
Save as PDF

Page ID: 227

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Six Basic Functions

Below are six basic functions:

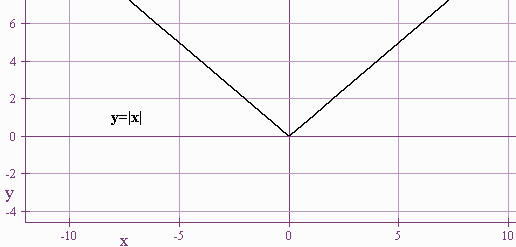
$SHIFT.HTM_txt_absx.gif$
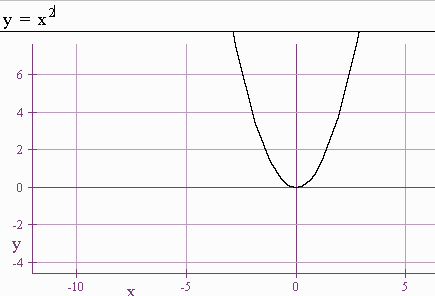
$xsquare.gif$
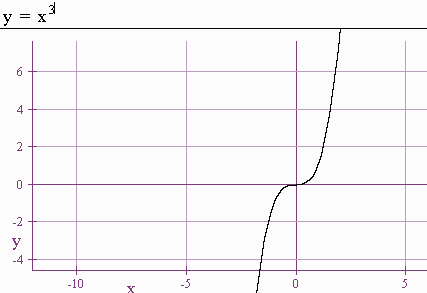
$xCube.gif$
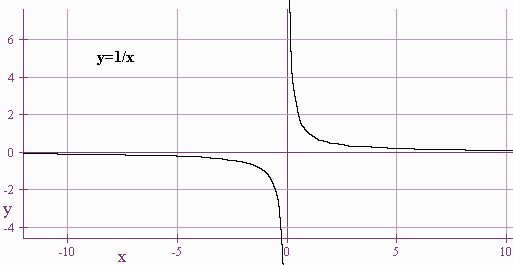
$SHIFT.HTM_txt_oneOverX.gif$
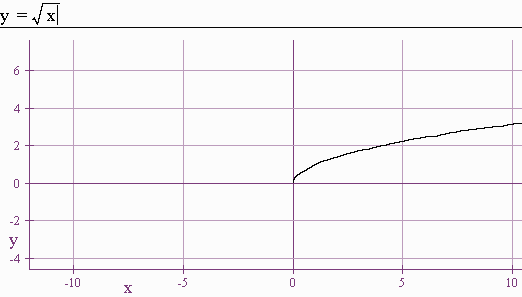
$rootx.gif$
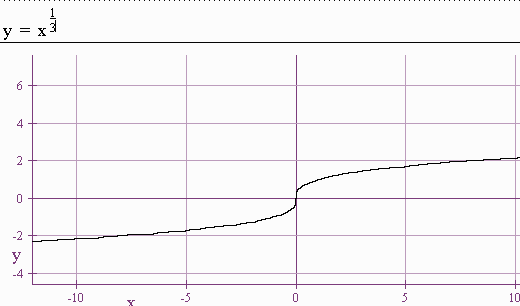
$cubeRoot.gif$

Memorize the shapes of these functions.

2. Horizontal Shifting

Consider the graphs

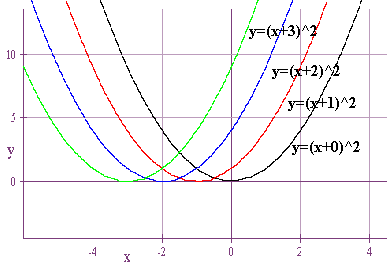
$SHIFT.HTM_txt_RtShift.gif$

$y =$

$(x+0)^2$
$(x+1)^2$
$(x+2)^2$
$(x+3)^2$

Exercise

Use the list features of a calculator to sketch the graph of

$y = \dfrac{1}{ [x - \{0,1,2,3\}] }$

Horizontal Shifting Rules

Rule 1: $f(x - a) = f(x)$ shifted $a$ units to the right.
Rule 2: $f(x + a) = f(x)$ shifted $a$ units to the left.

3. Vertical Shifting

Consider the graphs

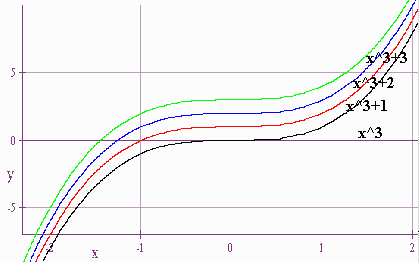
$SHIFT.HTM_txt_vertShft.gif$

$y =$

$x^3$
$x^3+ 1$
$x^3 + 2$
$x^3 + 3$

Exercise

Use the list features of a calculator to sketch the graph of

$y = x^3 - \{0,1,2,3\}$

Vertical Shifting Rules

Rule 3: $f(x ) + a = f(x)$ shifted a units up.
Rule 4: $f(x) - a = f(x)$ shifted a units down.

4. Reflecting About the x-axis

Consider the graphs of

$y = x^2$ and $y = -x^2$.

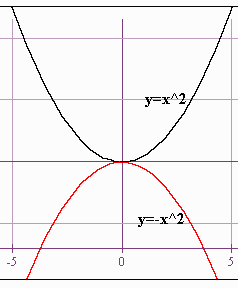
$SHIFT.HTM_txt_xReflect.gif$

x-Axis Reflection Rule

Rule 5: $-f(x) = f(x)$ reflected about the x-axis.

5. Reflecting About the y-axis

Exercise

Use the calculator to graph

$y=\sqrt{x}$

and
$y=\sqrt{-x}$

y-Axis Reflection Rule

Rule 6: $f(-x ) = f(x)$ reflected about the y-axis.

6. Stretching and Compressing

Exercise

Graph the following:

$y = \{1,2,3,4\}x^3$

$y = {1/2,1/3,1/4,1/5}x^3$

Stretching and Compression rules:

Rule 7: $cf(x ) = f(x)$ (for $c > 1$) stretched vertically.
Rule 8: $cf(x ) = f(x)$ (for $c < 1$) compressed vertically.

Exercise

Graph the following

$y = x^2 - 10$
$y = \sqrt{x - 2}$
$y = -|x - 5| + 3$

We will do some examples (including the graph of the winnings for the gambler and for the casino).

7. Increasing and Decreasing Functions

Definition

A function is called increasing if as an object moves from left to right, it is moving upwards along the graph. Or equivalently,

If $x < y$, then $f(x) < f(y)$.

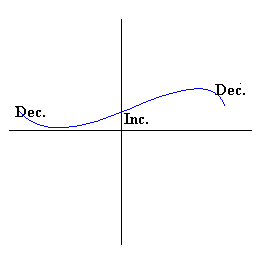
$SHIFT.HTM_txt_incDec.gif$

Example 1

The curve

\[y = x^2\]

is increasing on $(0,\infty)$ and decreasing on $(-\infty,0)$.

Contributors

Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.