1.4: Composition and Inverses

Last updated
Save as PDF

Page ID: 224

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\dsum}{\displaystyle\sum\limits} $

$ \newcommand{\dint}{\displaystyle\int\limits} $

$ \newcommand{\dlim}{\displaystyle\lim\limits} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$\newcommand{\longvect}{\overrightarrow}$

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\ket}[1]{\left| #1 \right>}$
$\newcommand{\bra}[1]{\left< #1 \right|}$
$\newcommand{\braket}[2]{\left< #1 \vphantom{#2} \right| \left. #2 \vphantom{#1} \right>}$
$\newcommand{\braopket}[3]{\left< #1 \vphantom{#2}\vphantom{#3} \right| #2 \vphantom{#1}\vphantom{#3} \left| #3 \vphantom{#1}\vphantom{#2} \right>}$
$\newcommand{\qmvec}[1]{\mathbf{\vec{#1}}}$
$\newcommand{\op}[1]{\hat{\mathbf{#1}}}$
$\newcommand{\expect}[1]{\langle #1 \rangle}$
$\newcommand{\dfn}[1]{\emph{\textbf{#1}}}$

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Composition of Functions

Example $\PageIndex{1}$

Sociologists in Holland determine that the number of people $y$ waiting in a water ride at an amusement park is given by

\[y = \dfrac{1}{50}C^2 + C + 2 \nonumber \]

where $C$ is the temperature in degrees $C$. The formula to convert Fahrenheit to Celsius $C$ is given by

\[C = \dfrac{5}{9}F + \dfrac{160}{9}. \nonumber \]

To get a function of $F$ we compose the two function:

\[y(C(F)) = \left(\dfrac{1}{50}\right)\left[\dfrac{5}{9}F + \dfrac{160}{9}\right]^2 + \left[\dfrac{5}{9}F + \dfrac{160}{9}\right] + 2 \nonumber \]

Exercise $\PageIndex{1}$

$f(x) = 3x + 2$
$g(x) = 2x^2 + 1$
$h(x) = \sqrt{x-2}$
$c(x) = 4$

Find

$f(g(x))$
$f(h(x))$
$f(f(x))$
$h(c(x))$
$c(f(g(h(x))))$

1-1 Functions

Definition: 1-1 (one-to-one)

A function $f(x)$ is 1-1 if

\[f(a) = f(b)\]

implies that

\[a = b.\]

Example $\PageIndex{2}$

\[f(x) = 3x + 1 \nonumber\]

then

\[3a + 1 = 3b + 1 \nonumber\]

implies that

\[3a = 3b \nonumber\]

hence

\[a = b \nonumber\]

therefore $f(x)$ is 1-1.

Example $\PageIndex{3}$

\[f(x) = x^2 \nonumber\]

then

\[a^2 = b^2 \nonumber\]

implies that

\[a^2-b^2 = 0 \nonumber\]

or that

\[(a - b)(a + b) = 0 \nonumber\]

hence

\[a = b \text{ or } a = -b \nonumber\]

For example

\[f (2) = f (-2) = 4 \nonumber\]

Hence $f(x)$ is not 1-1.

Horizontal Line Test

If every horizontal line passes through $f(x)$ at most once then $f(x)$ is 1-1.

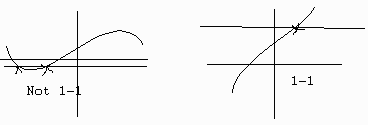
$oneone.gif$

Inverse Functions

Definition: Inverse function

A function $g(x)$ is an inverse of $f(x)$ if

\[f(g(x)) = g(f(x)) = x.\]

Example $\PageIndex{4}$

The volume of a lake is modeled by the equation

\[V(t) = \dfrac{1}{125}h^3. \nonumber\]

Show that the inverse is

\[h(N) = 5V^{\frac{1}{3}}. \nonumber\]

Solution: We have

\[h(V(h)) = 5(\dfrac{1}{125}h^3)^{\frac{1}{3}} = \dfrac{5}{5}h = h \nonumber\]

and

\[v(h(V)) = \dfrac{1}{125}(5V^{\frac{1}{3}})^3 = \dfrac{1}{125}(125V) = V. \nonumber\]

Step by Step Process for Finding the Inverse

Interchange the variables
Solve for $y$
Write in terms of $f^{-1}(x)$

Example$\PageIndex{5}$

Find the inverse of

\[f (x) = y = 3x^3 - 5 \nonumber\]

Solution

\[\begin{align} x &= 3y^3 - 5 \\ x + 5 &= 3y^3 \\ \dfrac{(x + 5)}{3} &= y^3 ,\\ \left[\dfrac{(x + 5)}{3}\right]^{\frac{1}{3}}&=y \end{align}\]

\[f^{-1}(x) = \left[\dfrac{(x + 5)}{ 3 }\right]^{\frac{1}{3}}. \nonumber\]

Graphing

To graph an inverse we draw the $y = x$ line and reflect the graph across this line.

To interactively view the graph of an inverse click here:

mathcsjava.emporia.edu/~greenlar/Inverse/inverse.html

Contributors and Attributions

Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.

Search

Text Color

Text Size

Margin Size

Font Type