3.3: Repeated Roots and Reduction of Order
- Page ID
- 402
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Now that we know how to solve second order linear homogeneous differential equations with constant coefficients such that the characteristic equation has distinct roots (either real or complex), the next task will be to deal with those which have repeated roots. We proceed with an example.
Solve \[y'' - 12y' + 36y = 0. \]
Solution
The characteristic equation is
\[ r^2 - 12r + 36 = 0 \]
or
\[ {(r - 6)}^2 = 0. \]
We have only the root \(r = 6\) which gives the solution
\[y_1 = e^{6t}.\]
By general theory, there must be two linearly independent solutions to the differential equation. We have found one and now search for a second. Fortunately, a long time ago a mathematician named D'Alembert came up with a way to find the second linearly independent solution. His idea was to write the second solution in the form
\[ y_2 = v(t)e^{6t} \]
and solve for \(v(t)\). The derivatives are
\[y'_2 = v'(t)e^{6t} + 6v(t)e^{6t} = {\left ( v'(t) + 6v(t) \right ) }^{6t},\]
\[y''_2 = { \left ( v''(t) +6v'(t) \right )}e^{6t} + 6{ \left (v'(t) + 6v(t) \right ) }e^{6t} = {\left ( v''(t) + 12v'(t) + 36v(t) \right ) }^{6t}.\]
Since \(y_2\) is a solution to the differential equation, we can plug it in to get
\[(v''(t) + 12v'(t) + 36v(t))e^6t - 12[ (v'(t) + 6v(t))e^6t] + 36v(t)e^6t\]
\[ = [v''(t) + 12v'(t) + 36v(t) - 12v'(t) - 72v(t) +36v(t)]e^{6t} \]
\[ = v''(t)e^{6t} = 0. \]
Since an exponential is never zero, we can conclude that
\[v''(t) = 0. \]
Integrating twice gives
\[ v(t) = C_2t + C_3 \]
For \( C_2 = 0 \) and \( C_3 = 1\), we get the original solution from the characteristic equation. However, for \( c_2 = 1 \) and \( C_3 = 0 \), we get
\[ y_2 = v(t)e^{6t} = te^{6t}.\]
We need to check that \(y_1\) and \(y_2\) are linearly independent. We compute the Wronskian
\[ W = ( e^{6t})(e^{6t} + 6te^{6t}) - (6e^{6t})(te^{6t}) = e^{12t} + 6te^{12t}6te^{12t} = e^{12t}.\]
Since the Wronskian is an exponential, it is nonzero and the two solutions are linearly independent. The general solution is
\[ y = C_1e^{6t} + C_2te^{6t}. \]
Let \( ay'' + by' + cy = 0 \) be a differential equation such that the characteristic equation has the repeated root \(r\). That is
\[ b^2 - 4ac = 0. \]
Then the general solution to the differential equation is given by
\[ y = c_1e^{rt} + c_2te^{rt}. \]
To prove this theorem, we just go through the same steps as in the example above. We will leave out the general proof here. The proof can be found at http://www.math.colostate.edu/m340/notes/ODEI/node4.html among other places.
Find the solution to
\[ y'' + 10y' + 25y = 0 \;\;\; \text{given}, \; y(0) = 2, \;\; y'(0) = 3 .\]
Solution
The characteristic equation is
\[ r^2 + 10r + 25 = {(r + 5)}^2 = 0. \]
This has the repeated root of \(r = -5\). The general solution is
\[ y = C_1e^{-5t} + C_2te^{-5t}. \]
We use the initial values to determine the constants
\[ 2 = C_1e^{-5(0)} + C_2 (0)e^{-5(0)} = C_1. \]
Taking the derivative gives
\[ y' = -10e^{-5t} + C_2( e^{-5t} - 5te^{-5t}).\]
Plugging in the initial value gives
\[ 3 = -10 + C_2(1 - 0)\]
\[C_2 = 13. \]
The final solution is
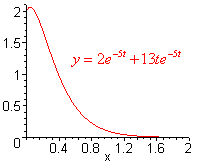
\[ y = 2e^{-5t} + 13te^{-5t} \]
which is pictured below.
When there are repeated roots, one of the linearly independent solutions was easy to find, while for the other solution we assumed that it had the form of a function times the known solution. This approach works more generally.
If \(y_1\) is a known solution to a homogeneous linear differential equation, then we can seek a second linearly independent solution by writing \(y_2 = v(t)y_1\).
This is demonstrated with an example.
Given that \(y_1 = t\) is a solution to the differential equation
\[ t^2y'' + 2ty' - 2y = 0. \label{Ex3eq1}\]
Find the general solution.
Solution
We write
\[ y_2 = vt\]
\[ y'_2 = v't + v\]
\[y''_2 = v''t + v' + v' = v''t + 2v' \]
Substituting back into the differential equation (Equation \ref{Ex3eq1}) gives
\[ \begin{align*} t^2(v''t + 2v') + 2t(v't + v) - 2(vt) &= 0 \\[4pt] t^3v'' + 2t^2v' + 2t^2v' + 2tv - 2tv &= 0 \\[4pt] t^3v'' + 4t^2v' &= 0 \\[4pt] tv'' + 4v' &= 0. \end{align*}\]
Notice that the \(''v''\) term dropped out. This will always be the case. We can now let
\[ u = v', \; u' = v''. \nonumber\]
Substituting gives
\[ tu' + 4u = 0. \nonumber\]
This is a first order differential equation (hence the title "Reduction of Order"). We can separate to get
\[ \frac{du}{u} = 4\frac{dt}{t}. \nonumber\]
Now integrate to get
\[ ln \left \vert u \right \vert = 4 ln \left \vert t \right \vert + C \]
\[ u = Ct^4 \]
\[ v' = Ct^4 \]
\[ v = Ct^5. \]
We can conclude that a second linearly independent solution is given by
\[ y_2 = (t^5)(t) = t^6. \nonumber\]
The general solution is
\[ y = C_1t + C_2t^6. \nonumber\]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


