9.2: Union, Intersection, and Complement
- Page ID
- 62021
Commonly sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.
However, before we talk about multiple sets interacting, we first introduce the idea of a set's complement.
The complement of a set A contains everything that is not in the set A.
The complement is notated \(A^c\) or \(\bar{A}\).
Notice that, without context, it is hard (or even impossible) to describe \(A^{c}\), since everything from the color fuchsia to puppies and peanut butter are included in the complement of a random set. For this reason, complements are usually only used when we have a universal set in place (or when we are also taking the intersection of sets, which is introduced later in this section).
A universal set \(U\) is a set that contains all the elements we are interested in. This would have to be defined by the context.
A set complement is relative to the universal set, so \(A^{c}\) contains all the elements in the universal set that are not in \(A\).
More formally, \(x \in A^c\) if \(x \in U\) and \(x \not\in A\)
- If we were discussing searching for books, the universal set might be all the books in the library.
- If we were grouping your Facebook friends, the universal set would be all your Facebook friends.
- If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers
Suppose the universal set is \(U={1,2,3,4,5,6,7,8,9\) (all whole numbers from \(1\) to \(9 \)). If \(A=\{1,2,4\}\), then
\(A^{c}=\{3,5,6,7,8,9\}\)
The union of two sets contains all the elements contained in either set (or both sets).
The union is notated \(A \cup B\)
More formally, \(x \in A \cup B\) if \(x \in A\) or \(x \in B\) (or both)
The intersection of two sets contains only the elements that are in both sets.
The intersection is notated \(A \cap B\)
More formally, \(x \in A \cap B\) if \(x \in A\) and \(x \in B\)
Consider the sets:
\(\quad A=\{\text { red, green, blue }\} \quad B=\{\text { red, yellow, orange }\} \quad C=\{\text { red, orange, yellow, green, blue, purple }\}\)
- Find \(A \cup B\)
- Find \(A \cap B\)
- Find \(A^{c} \cap C\)
Solution
a) The union contains all the elements in either set: \(A \cup B=\{\text { red, green, blue, yellow, orange }\}\)
Notice we only list red once.
b) The intersection contains all the elements in both sets: \(A \cap B=\{\text { red }\}\)
c) Here we're looking for all the elements that are not in set \(A\) and are also in \(C\).
\(A^{c} \cap C=\{\text { orange, yellow, purple }\}\)
Notice that in the example above, we do not need a universal set since we are using complement together with the intersection operation.
Using the sets from the previous example, find \(A \cup C\) and \(B^{c} \cap A\)
- Answer
-
\(A \cup C=\{\text { red, orange, yellow, green, blue purple }\}\)
\(B^{c} \cap A=\{\text { green, blue }\}\)
As we saw earlier with the expression \(A^{c} \cap C,\) set operations can be grouped together. Grouping symbols can be used like they are with arithmetic - to force an order of operations.
Suppose
\(H=\{\text { cat, dog, rabbit, mouse }\}, F=\{\text { dog, cow, duck, pig, rabbit }\} \quad W=\{\text { duck, rabbit, deer, frog, mouse }\}\)
- Find \((H \cap P) \cup W\)
- Find \(H \cap(F \cup W)\)
- Find \((H \cap P) \cap W\)
Solution
a) We start with the intersection: \(H \cap F=\{\text { dog, rabbit }\}\)
Now we union that result with \(W:(H \cap F) \cup W=\{\text{dog, duck, rabbit, deer, frog, mouse }\}\)
b) We start with the union: \(F \cup W=\{\text{dog, cow, rabbit, duck, pig, deer, frog, mouse }\}\)
Now we intersect that result with \(H: H \cap(F \cup W)=\{\text { dog, rabbit, mouse }\}\)
c) We start with the intersection: \(H \cap F=\{\mathrm{dog}, \text { rabbit }\}\)
Now we want to find the elements of \(W\) that are not in \(\mathrm{H} \cap F\)
\((H \cap P)^{c} \cap W=\{\text { duck, deer, frog, mouse }\}\)
CARDINALITY
Recall that the cardinality of a set is the number of elements in a set. We now discuss how to think about cardinality when taking the union, intersection, or complement of sets.
Let \(A=\{1,2,3,4,5,6\}\) and \(B=\{2,4,6,8\}\)
What is the cardinality of the set \(A \cup B\)? The set \(A \cap B ?\)
Solution
The cardinality of \(A \cup B\) is \(7,\) since \(A \cup B=\{1,2,3,4,5,6,8\}\), which contains 7 elements.
The cardinality of \(A \cap B\) is 3 , since \(A \cap B=\{2,4,6\}\), which contains 3 elements.
Sometimes we may be interested in the cardinality of the union or intersection of sets, but not know the actual elements of each set. This is common in surveying.
A survey asks 200 people “What beverage do you drink in the morning”, and offers choices:
- Tea only
- Coffee only
- Both coffee and tea
Suppose 20 report tea only, 80 report coffee only, 40 report both. How many people drink tea in the morning? How many people drink neither tea or coffee?
Solution
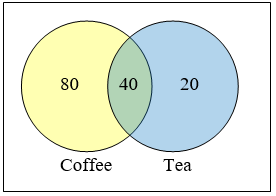We can find the people who drink tea by adding those who drink only tea to those who drink both: \(20+40=60\) people.
We can also see that those who drink neither are those not contained in the any of the three other groupings, so we can count those by subtracting from the cardinality of the universal set, 200.
\(200-20-80-40=60\) people who drink neither.
Note that this question can most easily be answered by creating a Venn diagram (discussed in the next section and pictured here).
A survey asks 100 people: Which online services have you used in the last month:
- Have used both
The results show 35 of those surveyed have used Twitter, 30 have used Facebook, and 20 have used both. How many people have used neither Twitter or Facebook?
Solution
Let \(T\) be the set of all people who have used Twitter, and \(F\) be the set of all people who have used Facebook. Notice that while the cardinality of \(F\) is \(30\) and the cardinality of \(T\) is \(35 \), the cardinality of \(F \cup T\) is not simply \(30+35\), since that would count those who use both services twice. To find the cardinality of \(F \cup T\), we can add the cardinality of \(F\) and the cardinality of \(T\), then subtract those in intersection that we've counted twice. In symbols,
\(n(F \cup T)=n(F)+n(T)-n(F \cap T)\)
\(n(F \cup T)=30+35-20=45\)
Now, to find how many people have not used either service, we're looking for the cardinality of \((F \cup T)^{c}\). Since the universal set contains \(100\) of people and the cardinality of \(F \cup T=45\), the cardinality of \((F \cup T)^{c}\) must be the other \(55\).
The previous example illustrated two important properties
\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
\(n\left(A^{c}\right)=n(U)-n(A)\)
Notice that the first property can also be written in an equivalent form by solving for the cardinality of the intersection:
\(n(A \cap B)=n(A)+n(B)-n(A \cup B)\)
Suppose 500 people are surveyed regarding their music listening habits. The survey found that find 420 people said they listen to music using streaming services, 140 people said they listen to music on the radio, and 110 people said they listen to both the radio and streaming services.
(a) How many people listened using either streaming services or the radio?
(b) How many people listened using the radio, but not streaming services?
- Answer
-
(a) Letting \(S\) be the set of streaming listeners and \(R\) be the set of radio listeners, this can formulated as finding \(n(S\cup R)\). Since \(n(S) = 420\), \(n(R)=140\), and \(n(S\cap R) = 110\), we can use our formula to get:
\(n(S \cup R) = 420 + 140 - 110 = 450\) people
(b) This can be formulated as \(n(R \cap S^c)\). In other words, we need to subtract the people who use both the radio and streaming from the set of people who listen to the radio. In other words,
\(n(R \cap S^c) = n(R) - n(R \cap S) = 140 - 110 = 30\) people.