9.3: Venn Diagrams

Last updated
Save as PDF

Page ID: 62022

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18^th century. These illustrations now called Venn Diagrams.

Venn Diagram

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets.

Basic Venn diagrams can illustrate the interaction of two or three sets.

Example 1

Create Venn diagrams to illustrate $A \cup B, A \cap B,$ and $A^{c} \cap B$

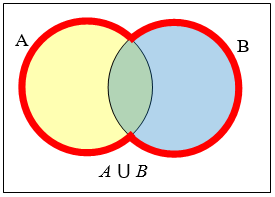$A Venn diagram showing two overlapping sets A and B. The region included in either set is highlighted.$ $A \cup B$ contains all elements in either set.

$A \cup B$ contains all elements in either set.

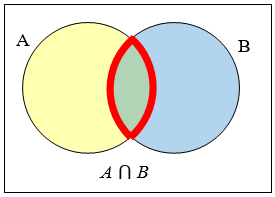
$A Venn diagram showing two overlapping sets A and B. The overlapping region included in both sets is highlighted.$

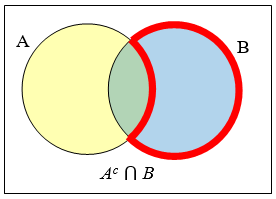$A Venn diagram showing two overlapping sets A and B. The region included only in B but not A is highlighted.$ $A \cap B$ contains only those elements in both sets - in the overlap of the circles.

Example 2

Use a Venn diagram to illustrate $(H \cap P)^{c} \cap W$

We'll start by identifying everything in the set $\mathrm{H} \cap P$

$A Venn diagram of three sets H F and W are shown overlapping. The region where H and F overlap is highlighted.$

Now, $(H \cap P)^{c} \cap W$ will contain everything not in the set identified above that is also in set $W$

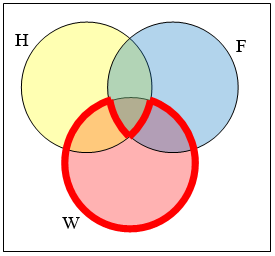
$A Venn diagram of three sets H F and W are shown overlapping. The region in set W is highlighted, with the exception of the part that also lies in both F and H. In other words, all of W, except for the part where all three overlap.$

Example 3

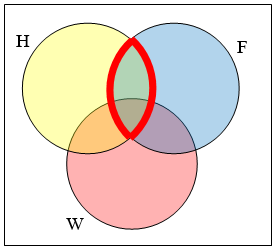
Create an expression to represent the outlined part of the Venn diagram shown.

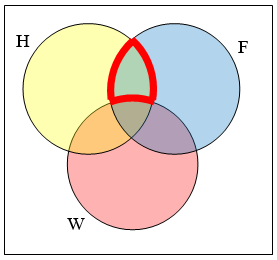$A Venn diagram of three sets H F and W are shown overlapping. The region where H and F overlap, but W does not, is highlighted.$ The elements in the outlined set are in sets $\mathrm{H}$ and $F$, but are not in set $W$. So we could represent this set as $H \cap F \cap W$

Try it Now 1

Create an expression to represent the outlined portion of the Venn diagram shown

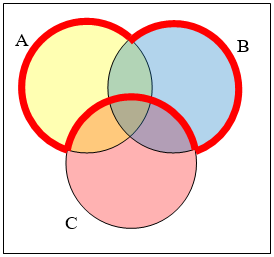
$A Venn diagram of three sets A B and C are shown overlapping. The region highlighted includes anything in A or anything in B, excluding anything also in C$

Answer: $A \cup B \cap C^{c}$

VENN DIAGRAMS AND CARDINALITY

In the last section, we got formulas for cacluating the cardinality of unions and intersections of two sets. Venn diagrams are very useful for visually orgainzing information relating to cardinality (especially with more than two sets).

Example 4

Fifty students were surveyed, and asked if they were taking a social science (SS), humanities (HM) or a natural science (NS) course the next quarter.

$\begin{array}{ll} \text{21 were taking a SS course} & \text{26 were taking a HM course} \\ \text{19 were taking a NS course} & \text{9 were taking SS and HM} \\ \text{7 were taking SS and NS} & \text{10 were taking HM and NS} \\ \text{3 were taking all three} & \text{7 were taking none} \end{array}$

How many students are only taking a SS course?

Solution

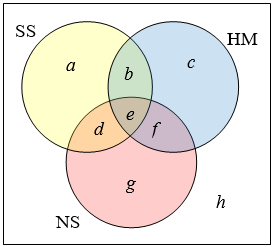$A Venn diagram of three circles overlapping, labeled SS, HM, and NS. The part only in SS is labeled a. The overlap of SS and HM only is labeled b. The part only in HM is labeled c. The overlap of SS and NS only is labeled d. The overlap of all three is labeled e. The overlap of HM and NS only is labeled f. The part in NS only is labeled g. The part outside all three is labeled h.$ It might help to look at a Venn diagram.

From the given data, we know that there are 3 students in region $e$ and 7 students in region $h$

since 7 students were taking a $S S$ and $N S$ course, we know that $n(d)+n(e)=7$. since we know there are 3 students in region 3 , there must be
$7-3=4$ students in region $d$

Similarly, since there are 10 students taking $\mathrm{HM}$ and $\mathrm{NS}$, which includes regions $e$ and $f$, there must be

$10-3=7$ students in region $f$

Since 9 students were taking $\mathrm{SS}$ and $\mathrm{HM}$, there must be $9-3=6$ students in region $b$

Now, we know that 21 students were taking a SS course. This includes students from regions $a, b, d,$ and $e .$ since we know the number of students in all but region $a,$ we can determine that $21-6-4-3=8$ students are in region $a$

8 students are taking only a SS course.

Try it Now 2

One hundred fifty people were surveyed and asked if they believed in UFOs, ghosts, and Bigfoot.

$\begin{array}{ll} \text{43 believed in UFOs} & \text{44 believed in ghosts} \\ \text{25 believed in Bigfoot} & \text{10 believed in UFOs and ghosts} \\ \text{8 believed in ghosts and Bigfoot} & \text{5 believed in UFOs and Bigfoot} \\ \text{2 believed in all three} & \text{} \end{array}$

(a) How many people surveyed believed in at least one of these things?

(b) How many people believed in none of them?

Answer

$A Venn diagram of three overlapping circles labeled UFOs, Ghosts, and Bigfoot. The part only in UFOs is 30. The overlap of UFOs and Ghosts only is 8. The part in ghosts only is 28. The overlap of UFOs and bigfoot only is 3. The overlap of all three is 2. The overlap of ghosts and bigfoot only is 6. The part in bigfoot only is 14. The part outside all three is 59.$ (a) Starting with the intersection of all three circles, we work our way out. Since 10 people believe in UFOs and Ghosts, and 2 believe in all three, that leaves 8 that believe in only UFOs and Ghosts. We work our way out, filling in all the regions. Once we have, we can add up all those regions, getting 91 people in the union of all three sets, or 91 people who believe in at least one of these things.

(b) Since we already know from part (a) that 91 people believe in at least one of UFOs, ghosts, and bigfoot, we can substract this number from 150 (the cardinality of the universal set) to get the number of people who believe in none of them.This gives us $150-91=59$ who believe in none.

Search

Text Color

Text Size

Margin Size

Font Type

Solution