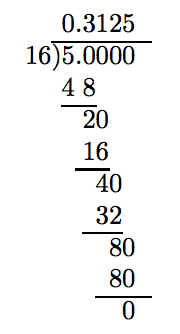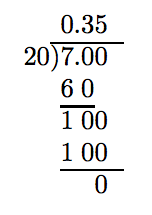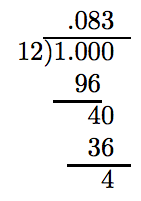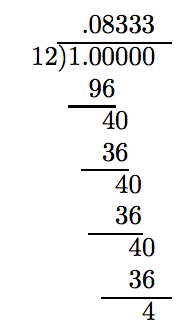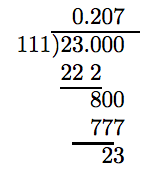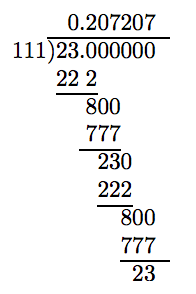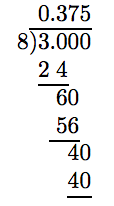3.6: Fractions and Decimals
- Page ID
- 35412
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When converting a fraction to a decimal, only one of two things can happen. Either the process will terminate or the decimal representation will begin to repeat a pattern of digits. In each case, the procedure for changing a fraction to a decimal is the same.
To change a fraction to a decimal, divide the numerator by the denominator. Hint: If you first reduce the fraction to lowest terms, the numbers will be smaller and the division will be a bit easier as a result.
Terminating Decimals
First reduce the fraction to lowest terms. If the denominator of the resulting fraction has a prime factorization consisting of strictly twos and/or fives, then the decimal representation will “terminate.”
Change 15/48 to a decimal.
Solution
First, reduce the fraction to lowest terms.
\[ \begin{aligned} \frac{15}{48} = \frac{3 \cdot 5}{3 \cdot 16} \\ = \frac{5}{16} \end{aligned}\nonumber \]
Next, note that the denominator of 5/16 has prime factorization 16 = 2·2·2·2. It consists only of twos. Hence, the decimal representation of 5/16 should terminate.
The zero remainder terminates the process. Hence, 5/16 = 0.3125.
Change 10/16 to a decimal.
- Answer
-
0.625
Change \(3 \frac{7}{20}\) to a decimal.
Solution
Note that 7/20 is reduced to lowest terms and its denominator has prime factorization 20 = 2 · 2 · 5. It consists only of twos and fives. Hence, the decimal representation of 7/20 should terminate.
The zero remainder terminates the process. Hence, 7/20 = 0.35. Therefore, \(3 \frac{7}{20}\) = 3.35.
Change \(7 \frac{11}{20}\) to a decimal.
- Answer
-
7.55
Repeating Decimals
First reduce the fraction to lowest terms. If the prime factorization of the resulting denominator does not consist strictly of twos and fives, then the division process will never have a remainder of zero. However, repeated patterns of digits must eventually reveal themselves.
Change 1/12 to a decimal.
Solution
Note that 1/12 is reduced to lowest terms and the denominator has a prime factorization 12 = 2 · 2 · 3 that does not consist strictly of twos and fives. Hence, the decimal representation of 1/12 will not “terminate.” We need to carry out the division until a remainder reappears for a second time. This will indicate repetition is beginning.
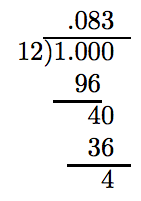
Note the second appearance of 4 as a remainder in the division above. This is an indication that repetition is beginning. However, to be sure, let’s carry the division out for a couple more places.
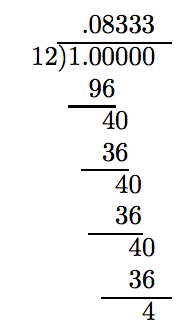
Note how the remainder 4 repeats over and over. In the quotient, note how the digit 3 repeats over and over. It is pretty evident that if we were to carry out the division a few more places, we would get
\[\frac{1}{12} = 0.833333 \cdots\nonumber \]
The ellipsis is a symbolic way of saying that the threes will repeat forever. It is the mathematical equivalent of the word “etcetera.”
Change 5/12 to a decimal.
- Answer
-
0.41666...
There is an alternative notation to the ellipsis, namely
\[ \frac{1}{12} = 0.08 \overline{3}.\nonumber \]
The bar over the 3 (called a “repeating bar”) indicates that the 3 will repeat indefinitely. That is,
\[0.08 \overline{3} = 0.083333 ....\nonumber \]
To use the repeating bar notation, take whatever block of digits are under the repeating bar and duplicate that block of digits infinitely to the right.
Thus, for example:
- \(5. \overline{345} = 5.3454545 ....\)
- \(0. \overline{142857} = 0.142857142857142857 ....\)
Although \(0.8 \overline{33}\) will also produce 0.8333333 ..., as a rule we should use as few digits as possible under the repeating bar. Thus, \(0.8 \overline{3}\) is preferred over \(0.8 \overline{33}\).
Change 23/111 to a decimal.
Solution
The denominator of 23/111 has prime factorization 111 = 3 ·37 and does not consist strictly of twos and fives. Hence, the decimal representation will not “terminate.” We need to perform the division until we spot a repeated remainder.
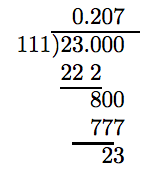
Note the return of 23 as a remainder. Thus, the digit pattern in the quotient should start anew, but let’s add a few places more to our division to be sure.
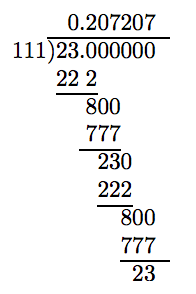
Aha! Again a remainder of 23. Repetition! At this point, we are confident that
\[ \frac{23}{111} = 0.207207 ....\nonumber \]
Using a “repeating bar,” this result can be written
\[ \frac{23}{111} = 0. \overline{207}.\nonumber \]
Change 5/33 to a decimal.
- Answer
-
0.151515...
Expressions Containing Both Decimals and Fractions
At this point we can convert fractions to decimals, and vice-versa, we can convert decimals to fractions. Therefore, we should be able to evaluate expressions that contain a mix of fraction and decimal numbers.
Simplify: \(- \frac{3}{8} - 1.25\).
Solution
Let’s change 1.25 to an improper fraction.
\[ \begin{aligned} 1.25 = \frac{125}{100} ~ & \textcolor{red}{ \text{ Two decimal places } \Rightarrow \text{ two zeroes.} \\ = \frac{5}{4} ~ & \textcolor{red}{ \text{ Reduce to lowest terms.}} \end{aligned}\nonumber \]
In the original problem, replace 1.25 with 5/4, make equivalent fractions with a common denominator, then subtract.
\[ \begin{aligned} - \frac{3}{8} - 1.25 = - \frac{3}{8} - \frac{5}{4} ~ & \textcolor{red}{ \text{ Replace 1.25 with 5/4.}} \\ = - \frac{3}{8} - \frac{5 \cdot \textcolor{red}{2}}{4 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions, LCD = 8.}} \\ = - \frac{3}{8} - \frac{10}{8} ~ & \textcolor{red}{ \text{ Simplify the numerator and denominator.}} \\ = - \frac{3}{8} + \left( - \frac{10}{8} \right) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = = \frac{13}{8} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Thus, −3/8 − 1.25 = −13/8.
Alternate Solution
Because −3/8 is reduced to lowest terms and 8 = 2 ·2 ·2 consists only of twos, the decimal representation of −3/8 will terminate.
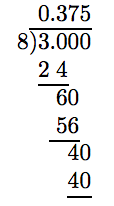
Hence, −3/8 = −0.375. Now, replace −3/8 in the original problem with −0.375, then simplify.
\[ \begin{aligned} - \frac{3}{8} - 1.25 = -0.375 - 1.25 ~ & \textcolor{red}{ \text{ Replace } -3/8 \text{ with } -0.375.} \\ =-0.375 + (-1.25) ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ = -1.625 ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Thus, −3/8 − 1.25 = −1.625.
Are They the Same?
The first method produced −13/8 as an answer; the second method produced −1.625. Are these the same results? One way to find out is to change −1.625 to an improper fraction.
\[ \begin{aligned} -1.625 = - \frac{1625}{1000} ~ & \textcolor{red}{ \text{ Three places } \Rightarrow \text{ three zeroes.}} \\ = - \frac{5 \cdot 5 \cdot 5 \cdot 5 \cdot 13}{2 \cdot 2 \cdot 2 \cdot 5 \cdot 5 \cdot 5} ~ & \textcolor{red}{ \text{ Prime factor.}} \\ = - \frac{13}{2 \cdot 2 \cdot 2} ~ & \textcolor{red}{ \text{ Cancel common factors.}} \\ = - \frac{13}{8} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]
Thus, the two answers are the same.
Simplify: \(− \frac{7}{8} − 6.5\)
- Answer
-
\(−7 \frac{3}{8}\) or −7.375
Simplify: \(-\frac{2}{3} + 0.35\).
Solution
Let’s attack this expression by first changing 0.35 to a fraction.
\[ \begin{aligned} - \frac{2}{3} + 0.35 = - \frac{2}{3} + \frac{35}{100} ~ & \textcolor{red}{ \text{ Change 0.35 to a fraction.}} \\ = - \frac{2}{3} + \frac{7}{20} ~ & \textcolor{red}{ \text{ Reduce 35/100 to lowest terms.}} \end{aligned}\nonumber \]
Find an LCD, make equivalent fractions, then add.
\[ \begin{aligned} = - \frac{2 \cdot 20}{3 \cdot 20} + \frac{7 \cdot 3}{20 \cdot 3} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 60.}} \\ = - \frac{40}{60} + \frac{21}{60} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = - \frac{19}{60} ~ & \textcolor{red}{ \text{ Add.}} \end{aligned}\nonumber \]
Then, \(-\frac{2}{3} +0.35 = - \frac{19}{60}\).
Simplify: \(-\frac{4}{9} + 0.25\)
- Answer
-
−7/36
In Example 6, we run into trouble if we try to change −2/3 to a decimal. The decimal representation for −2/3 is a repeating decimal (the denominator is not made up of only twos and fives). Indeed, −2/3 = \(−0. \overline{6}\). To add \(−0. \overline{6}\) and 0.35, we have to align the decimal points, then begin adding at the right end. But \(−0. \overline{6}\) has no right end! This observation leads to the following piece of advice.
When presented with a problem containing both decimals and fractions, if the decimal representation of any fraction repeats, its best to first change all numbers to fractions, then simplify.
Exercises
In Exercises 1-20, convert the given fraction to a terminating decimal.
1. \(\frac{59}{16}\)
2. \(\frac{19}{5}\)
3. \(\frac{35}{4}\)
4. \(\frac{21}{4}\)
5. \(\frac{1}{16}\)
6. \(\frac{14}{5}\)
7. \(\frac{6}{8}\)
8. \(\frac{7}{175}\)
9. \(\frac{3}{2}\)
10. \(\frac{15}{16}\)
11. \(\frac{119}{175}\)
12. \(\frac{4}{8}\)
13. \(\frac{9}{8}\)
14. \(\frac{5}{2}\)
15. \(\frac{78}{240}\)
16. \(\frac{150}{96}\)
17. \(\frac{25}{10}\)
18. \(\frac{2}{4}\)
19. \(\frac{9}{24}\)
20. \(\frac{216}{150}\)
In Exercises 21-44, convert the given fraction to a repeating decimal. Use the “repeating bar” notation.
21. \(\frac{256}{180}\)
22. \(\frac{268}{180}\)
23. \(\frac{364}{12}\)
24. \(\frac{292}{36}\)
25. \(\frac{81}{110}\)
26. \(\frac{82}{99}\)
27. \(\frac{76}{15}\)
28. \(\frac{23}{9}\)
29. \(\frac{50}{99}\)
30. \(\frac{53}{99}\)
31. \(\frac{61}{15}\)
32. \(\frac{37}{18}\)
33. \(\frac{98}{66}\)
34. \(\frac{305}{330}\)
35. \(\frac{190}{495}\)
36. \(\frac{102}{396}\)
37. \(\frac{13}{15}\)
38. \(\frac{65}{36}\)
39. \(\frac{532}{21}\)
40. \(\frac{44}{60}\)
41. \(\frac{26}{198}\)
42. \(\frac{686}{231}\)
43. \(\frac{47}{66}\)
44. \(\frac{41}{198}\)
In Exercises 45-52, simplify the given expression by first converting the fraction into a terminating decimal.
45. \(\frac{7}{4} − 7.4\)
46. \(\frac{3}{2} − 2.73\)
47. \(\frac{7}{5} + 5.31\)
48. \(− \frac{7}{4} + 3.3\)
49. \(\frac{9}{10} − 8.61\)
50. \(\frac{3}{4} + 3.7\)
51. \(\frac{6}{5} − 7.65\)
52. \(− \frac{3}{10} + 8.1\)
In Exercises 53-60, simplify the given expression by first converting the decimal into a fraction.
53. \(\frac{7}{6} − 2.9\)
54. \(− \frac{11}{6} + 1.12\)
55. \(− \frac{4}{3} − 0.32\)
56. \(\frac{11}{6} − 0.375\)
57. \(− \frac{2}{3} + 0.9\)
58. \(\frac{2}{3} − 0.1\)
59. \(\frac{4}{3} − 2.6\)
60. \(− \frac{5}{6} + 2.3\)
In Exercises 61-64, simplify the given expression.
61. \(\frac{5}{6} + 2.375\)
62. \(\frac{5}{3} + 0.55\)
63. \(\frac{11}{8} + 8.2\)
64. \(\frac{13}{8} + 8.4\)
65. \(− \frac{7}{10} + 1.2\)
66. \(− \frac{7}{5} − 3.34\)
67. \(− \frac{11}{6} + 0.375\)
68. \(\frac{5}{3} − 1.1\)
Answers
1. 3.6875
3. 8.75
5. 0.0625
7. 0.75
9. 1.5
11. 0.68
13. 1.125
15. 0.325
17. 2.5
19. 0.375
21. \(1.4 \overline{2}\)
23. \(30. \overline{3}\)
25. \(0.7 \overline{36}\)
27. \(5.0 \overline{6}\)
29. \(0. \overline{50}\)
31. \(4.0 \overline{6}\)
33. \(1. \overline{48}\)
35. \(0. \overline{38}\)
37. \(0.8 \overline{6}\)
39. \(25. \overline{3}\)
41. \(0. \overline{13}\)
43. \(0.7 \overline{12}\)
45. −5.65
47. 6.71
49. −7.71
51. −6.45
53. \(− \frac{26}{15}\)
55. \(− \frac{124}{75}\)
57. \(\frac{7}{30}\)
59. \(− \frac{19}{15}\)
61. \(\frac{77}{24}\)
63. 9.575
65. 0.5
67. \(− \frac{35}{24}\)