8.4: Triangles and Quadrilaterals
- Page ID
- 36594
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Follow these directions on your own:
- Draw any triangle on your paper.
- Draw a second triangle that is different in some way from your first one. Write down a sentence or two to say how it is different.
- Draw a third triangle that is different from both of your other two. Describe how it is different.
- Draw two more triangles, different from all the ones that came before.
Compare your triangles and descriptions with a partner. To make “different” triangles, you have to change some feature of the triangle. Make a list of the features that you or your partner changed.
Triangles are classified according to different properties. The point of learning geometry is not to learn a lot of vocabulary, but it’s useful to use the correct terms for objects, so that we can communicate clearly. Here’s a quick dictionary of some types of triangles.
| scalene | isosceles | equilateral |
|---|---|---|
 |
 |
 |
| all sides have different lengths | two sides have the same length | all three sides have the same length |
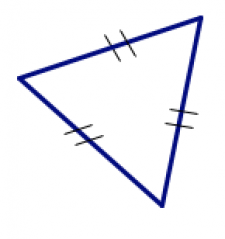
| acute | obtuse |
|---|---|
 |
 |
| all interior angles measure less than 90° | one interior angle measures more than 90° |
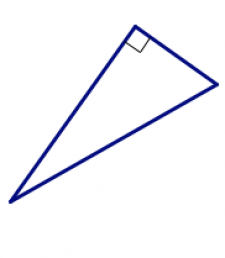
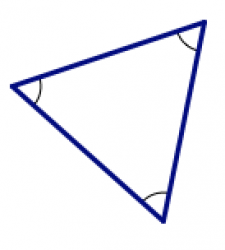
| right | equiangular |
|---|---|
 |
 |
| one interior angle measures exactly 90° | all interior angles have the same measure |
Remember that “geometry is the art of good reasoning from bad drawings.” That means you can’t always trust your eyes. If you look at a picture of a triangle and one side looks like it’s longer than another, that may just mean the drawing was done a bit sloppily.
Mathematicians either write down measurements or use tick marks to indicate when sides and angles are supposed to be equal.
If two sides have the same measurement or the same number of tick marks, you must believe they are equal and work out the problem accordingly, even if it doesn’t look that way to your eyes.
You can see examples of these in some of the pictures above. Another example is the little square used to indicate a right angle in the picture of the right triangle.
On Your Own
Work on the following exercises on your own or with a partner.
1. In the picture below, which sides are understood to have the same length (even if it doesn’t look that way in the drawing)?
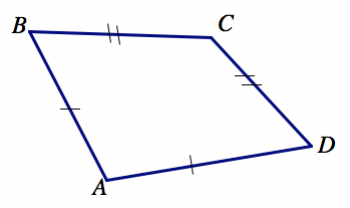
2. In the picture below, which angles are understood to have the same measure (even if if doesn’t look that way in the drawing)?
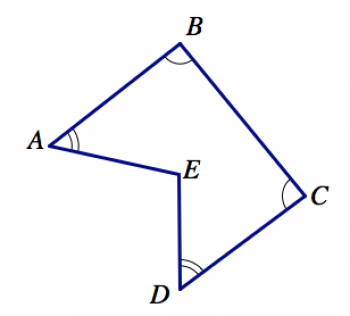
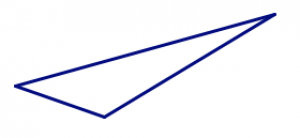
3. Here is a scalene triangle. Sketch two more scalene triangles, each of which is different from the one shown here in some way.
4. Here is an acute triangle. Sketch two more acute triangles, each of which is different from the one shown here in some way.
5. Here is an obtuse triangle. Sketch two more obtuse triangles, each of which is different from the one shown here in some way.
6. Here is a right triangle. Sketch two more right triangles, each of which is different from the one shown here in some way. Be sure to indicate which angle is 90°.
7. Here is an isosceles triangle. Sketch two more isosceles triangles, each of which is different from the one shown here in some way. Use tick marks to indicate which sides are equal.
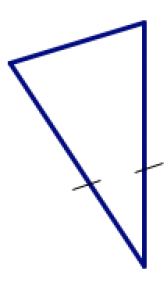
Angle Sum
By now, you have drawn several different triangles on your paper. Choose one of your triangles, and follow these directions:
- Using scissors, cut the triangle out.
- Tear (do not cut) off the corners, and place the three vertices together. Your should have something that looks a bit like this picture:
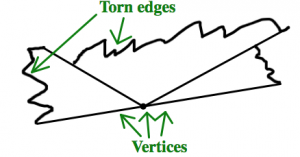
What do you notice? What does this suggest about the angles in a triangle?
You may remember learning that the sum of the angles in any triangle is 180°. In your class, you now have lots of examples of triangles where the sum of the angles seems to be 180°. But remember, our drawings are not exact. How can we be sure that our eyes are not deceiving us? How can we be sure that the sum of the angles in a triangle isn’t 181° or 178°, but is really 180° on the nose in every case?
What would convince you beyond all doubt that the sum of the angles in any triangle is 180°? Would testing lots of cases be enough? How many is enough? Could you ever test every possible triangle?
History: Euclid’s axioms
Often high school geometry teachers prove the sum of the angles in a triangle is 180°, usually using some facts about parallel lines. But (maybe surprisingly?) it’s just as good to take this as an axiom, as a given fact about how geometry works, and go from there. Perhaps this is less satisfying than proving it from some other statement, and if you’re curious you can certainly find a proof or your instructor can share one with you.
In about 300BC, Euclid[1] was the first mathematician (as far as we know) who tried to write down careful axioms and then build from those axioms rigorous proofs of mathematical truths.
Euclid
Euclid had five axioms for geometry, the first four of which seemed pretty obvious to mathematicians. People felt they were reasonable assumptions from which to build up geometric truths:
- Given two points, you can connect them with a straight line segment.
- Given a line segment, you can extend it as far as you like in either direction, making a line.
- Given a line segment, you can draw a circle having that segment as a radius.
- All right angles are congruent.
The fifth postulate bothered people a bit more. It was originally stated in more flowery language, but it was equivalent to this statement:
- The sum of the angles in a triangle is 180°.
It’s easy to see why this fifth axiom caused such a ruckus in mathematics. It seemed much less obvious than the other four, and mathematicians felt like they were somehow cheating if they just assumed it rather than proving it had to be true. Many mathematicians spent many, many years trying to prove this fifth axiom from the other axioms, but they couldn’t do it. And with good reason: There are other kinds of geometries where the first four axioms are true, but the fifth one is not!
For example, if you do geometry on a sphere — like a basketball or more importantly on the surface of the Earth — rather than on a flat plane, the first four axioms are true. But triangles are a little strange on the surface of the earth. Every triangle you can draw on the surface of the earth has an angle sum strictly greater than 180°. In fact, you can draw a triangle on the Earth that has three right angles[2], making an angle sum of 270°.
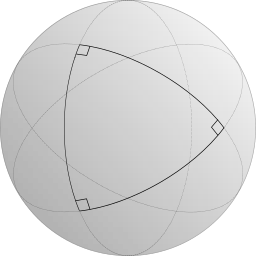
Triangle with three right angles on a sphere.
On a sphere like the Earth, the angle sum is not constant among all triangles. Bigger triangles have bigger angle sums, and smaller triangles have smaller angle sums, but even tiny triangles have angle sums that are greater than 180°.
The geometry you study in school is called Euclidean geometry; it is the geometry of a flat plane, of a flat world. It’s a pretty good approximation for the little piece of the Earth that we see at any given time, but it’s not the only geometry out there!
Triangle Inequality
Make a copy of these strips of paper and cut them out. They have lengths from 1 unit to 6 units. You may want to color the strips, write numbers on them, or do something that makes it easy to keep track of the different lengths.
Repeat the following process several times (at least 10) and keep track of the results (a table has been started for you).
- Pick three strips of paper. (The lengths do not have to be all different from each other; that’s why you have multiple copies of each length.)
- Try to make a triangle with those three strips, and decide if you think it is possible or not. (Don’t overlap the strips, cut them, or fold them. The length of the strips should be the length of the sides of the triangle.)
| Length 1 | Length 2 | Length 3 | Triangle? |
|---|---|---|---|
| 4 | 3 | 2 | yes |
| 4 | 2 | 1 | no |
| 4 | 2 | 2 | ?? |
Your goal is to come up with a rule that describes when three lengths will make a triangle and when they will not. Write down the rule in your own words.
Compare your rule with other students. Then use your rule to answer the following questions. Keep in mind the goal is not to try to build the triangle, but to predict the outcome based on your rule.
- Suppose you were asked to make a triangle with sides 40 units, 40 units, and 100 units long. Do you think you could do it? Explain your answer.
- Suppose you were asked to make a triangle with sides 2.5 units, 2.6 units, and 5 units long. Do you think you could do it? Explain your answer.
You probably came up with some version of this statement:
The sum of the lengths of two sides in a triangle is greater than the length of the third side.
Of course, we know that in geometry we should not believe our eyes. You need to look for an explanation. Why does your statement make sense?
Remember that “geometry is the art of good reasoning from bad drawings.” Our materials weren’t very precise, so how can we be sure this rule we’ve come up with is is correct?
Well in this case, the rule is really just the same as the saying “the shortest distance between two points is a straight line.” In fact, this is exactly what we mean by the words straight line in geometry.
SSS Congruence
We say that two triangles (or any two geometric objects) are congruent if they are exactly the same shape and the same size. That means that if you could pick one of them up and move it to put down on the other, they would exactly overlap.
Repeat the following process several times and keep track of the results.
- Pick three strips of paper that will definitely form a triangle.
- Try to make two different (non-congruent) triangles with the same three strips of paper. Record if you were able to do so.
Repeat the following process several times and keep track of the results.
- Pick four strips of paper and form a quadrilateral with them. (If your four strips do not form a quadrilateral, pick another four strips.)
- Try to make two different (non-congruent) quadrilaterals with the same four strips of paper. Record if you were able to do so.
What do you notice from Problems 4 and 5? Can you make a general statement to describe what’s going on? Can you explain why your statement makes sense?
You probably came up with some version of this statement:
If two triangles have the same side lengths, then the triangles are congruent.
This most certainly is not true for quadrilaterals. For example, if you choose four strips that are all the same length, you can make a square:
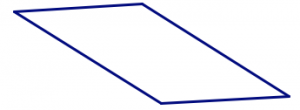
But you can also squish that square into a non-square rhombus. (Try it!)
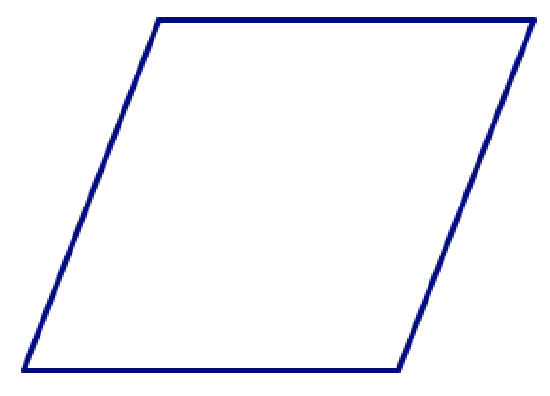
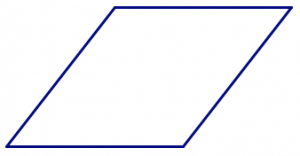
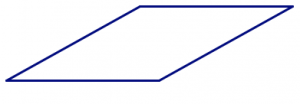
If you don’t choose four lengths that are all the same, in addition to “squishing” the shape, you can rearrange the sides to make different (non-congruent) shapes. (Try it!)
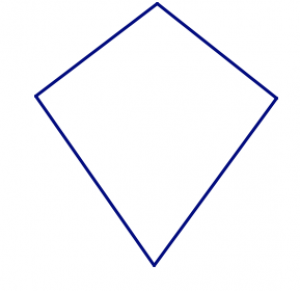
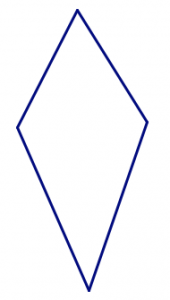
These two quadrilaterals have the same four side lengths in the same order.
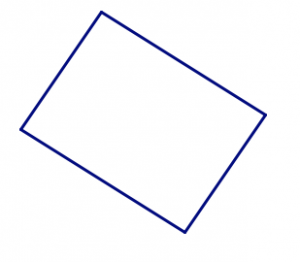
These two quadrilaterals have the same four side lengths as the two above, but the sides are in a different order.
But this can’t happen with triangles. Why not? Well, certainly you can’t rearrange the three sides. That would be just the same as rotating the triangle or flipping it over, but not making a new shape.
Why can’t the triangles “squish” the way a quadrilateral (and other shapes) can? Here’s one way to understand it. Imagine you pick two of your three lengths and lay them on top of each other, hinged at one corner.
This shows a longer purple dashed segment and a shorter green segment. The two segments are hinged at the red dot on the left.
Now imagine opening up the hinge a little at a time.
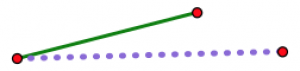
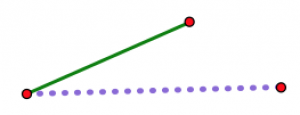
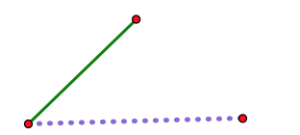
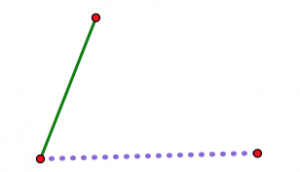
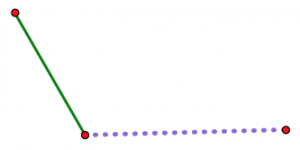
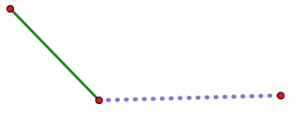
As the hinge opens up, the two non-hinged endpoints get farther and farther apart. Whatever your third length is (assuming you are actually able to make a triangle with your three lengths), there is exactly one position of the hinge where it will just exactly fit to close off the triangle. No other position will work.
- Portrait of Euclid from Wikimedia Commons, licensed under the Creative Commons Attribution 4.0 International license. ↵
- Image by Coyau / Wikimedia Commons, via Wikimedia Commons, licensed under Creative Commons Attribution-Share Alike 3.0 Unported. ↵