5.10: 5.5E and 5.6E U-Substitution Exercises

Last updated
Save as PDF

Page ID: 32822

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

5.5: Substitution

In the following exercises, find the antiderivative.

261) $\displaystyle∫(x+1)^4dx$

Answer:: $\displaystyle\frac{1}{5}(x+1)^5+C$

262) $\displaystyle∫(x−1)^5dx$

263) $\displaystyle∫(2x−3)^{−7}dx$

Answer:: $\displaystyle−\frac{1}{12(3−2x)^6}+C$

264) $\displaystyle∫(3x−2)^{−11}dx$

265) $\displaystyle∫\frac{x}{\sqrt{x^2+1}}dx$

Answer:: $\displaystyle\sqrt{x^2+1}+C$

266) $\displaystyle∫\frac{x}{\sqrt{1−x^2}}dx$

267) $\displaystyle∫(x−1)(x^2−2x)^3dx$

Answer:: $\displaystyle\frac{1}{8}(x^2−2x)^4+C$

268) $\displaystyle∫(x^2−2x)(x^3−3x^2)^2dx$

269) $\displaystyle∫cos^3θdθ(Hint:cos^2θ=1−sin^2θ)$

Answer:: $\displaystylesinθ−\frac{sin^3θ}{3}+C$

270) $\displaystyle∫sin^3θdθ(Hint:sin^2θ=1−cos^2θ)$

271) $\displaystyle∫x(1−x)^{99}dx$

Solution: $\displaystyle\frac{(1−x)^{101}}{101}−\frac{(1−x)^{100}}{100}+C$

272) $\displaystyle∫t(1−t^2)^{10}dt$

273) $\displaystyle∫(11x−7)^{−3}dx$

Answer:: $\displaystyle−\frac{1}{22(7−11x^2)}+C$

274) $\displaystyle∫(7x−11)^4dx$

275) $\displaystyle∫cos^3θsinθdθ$

Answer:: $\displaystyle−\frac{cos^4θ}{4}+C$
276) $\displaystyle∫sin^3θdθ;u=cosθ (Hint:sin^2θ=1−cos^2θ)$

(removed exercises 277- 280)

281) $\displaystyle∫\frac{x^2}{(x^3−3)^2}dx$

Answer:: $\displaystyle−\frac{1}{3(x^3−3)}+C$

In the following exercises, evaluate the definite integral.

292) $\displaystyle∫^1_0x\sqrt{1−x^2}dx$

293) $\displaystyle∫^1_0\frac{x}{\sqrt{1+x^2}}dx$

Answer:: $\displaystyle u=1+x^2,du=2xdx,\frac{1}{2}∫^2_1u^{−1/2}du=\sqrt{2}−1$

294) $\displaystyle∫^2_0\frac{t}{\sqrt{5+t^2}}dt$

295) $\displaystyle∫^1_0\frac{t}{\sqrt{1+t^3}}dt$

Answer:: $\displaystyle u=1+t^3,du=3t^2,\frac{1}{3}∫^2_1u^{−1/2}du=\frac{2}{3}(\sqrt{2}−1)$

296) $\displaystyle∫^{π/4}_0sec^2θtanθdθ$

297) $\displaystyle∫^{π/4}_0\frac{sinθ}{cos^4θ}dθ$

Answer:: $\displaystyle u=cosθ,du=−sinθdθ,∫^1_{1/\sqrt{2}}u^{−4}du=\frac{1}{3}(2\sqrt{2}−1)$

J5.5.1)

J5.5.2)

5.6: Integrals Involving Exponential and Logarithmic Functions

In the following exercises, compute each indefinite integral.

320) $\displaystyle ∫e^{2x}dx$

321) $\displaystyle ∫e^{−3x}dx$

Answer:: $\displaystyle \frac{−1}{3}e^{−3x}+C$

322) $\displaystyle ∫2^xdx$

323) $\displaystyle ∫3^{−x}dx$

Answer:: $\displaystyle −\frac{3^{−x}}{ln3}+C$

324) $\displaystyle ∫\frac{1}{2x}dx$

325) $\displaystyle ∫\frac{2}{x}dx$

Answer:: $\displaystyle ln(x^2)+C$ or $\displaystyle 2ln|x|+C$

326) $\displaystyle ∫\frac{1}{x^2}dx$

327) $\displaystyle ∫\frac{1}{\sqrt{x}}dx$

Answer:: $\displaystyle 2\sqrt{x}+C$

In the following exercises, find each indefinite integral by using appropriate substitutions.

328) $\displaystyle ∫\frac{lnx}{x}dx$

329) $\displaystyle ∫\frac{dx}{x(lnx)^2}$

Answer:: $\displaystyle −\frac{1}{lnx}+C$

336) $\displaystyle ∫xe^{−x^2}dx$

337) $\displaystyle ∫x^2e^{−x^3}dx$

Answer:: $\displaystyle \frac{−e^{−x^3}}{3}+C$

338) $\displaystyle ∫e^{sinx}cosxdx$

339) $\displaystyle ∫e^{tanx}sec^2xdx$

Answer:: $\displaystyle e^{tanx}+C$

340) $\displaystyle ∫e^{lnx}\frac{dx}{x}$

341) $\displaystyle ∫\frac{e^{ln(1−t)}}{1−t}dt$

Answer:: $\displaystyle t+C$

In the following exercises, evaluate the definite integral.

355) $\displaystyle ∫^2_1\frac{1+2x+x^2}{3x+3x^2+x^3}dx$

Answer:: $\displaystyle \frac{1}{3}ln(\frac{26}{7})$

356) $\displaystyle ∫^{π/4}_0tanxdx$

357) $\displaystyle ∫^{π/3}_0\frac{sinx−cosx}{sinx+cosx}dx$

Answer:: $\displaystyle ln(\sqrt{3}−1)$

358) $\displaystyle ∫^{π/2}_{π/6}cscxdx$

359) $\displaystyle ∫^{π/3}_{π/4}cotxdx$

Answer:: $\displaystyle \frac{1}{2}ln\frac{3}{2}$

In the following exercises, integrate using the indicated substitution.

360) $\displaystyle ∫\frac{x}{x−100}dx;u=x−100$

361) $\displaystyle ∫\frac{y−1}{y+1}dy;u=y+1$

Answer:: $\displaystyle y−2ln|y+1|+C$

362) $\displaystyle ∫\frac{1−x^2}{3x−x^3}dx;u=3x−x^3$

363) $\displaystyle ∫\frac{sinx+cosx}{sinx−cosx}dx;u=sinx−cosx$

Answer:: $\displaystyle ln|sinx−cosx|+C$

364) $\displaystyle ∫e^{2x}\sqrt{1−e^{2x}}dx;u=e^{2x}$

365) $\displaystyle ∫ln(x)\frac{\sqrt{1−(lnx)^2}}{x}dx;u=lnx$

Answer:: $\displaystyle −\frac{1}{3}(1−(lnx^2))^{3/2}+C$

In the following exercises, $\displaystyle f(x)≥0$ for $\displaystyle a≤x≤b$. Find the area under the graph of $\displaystyle f(x)$ between the given values a and b by integrating.

372) $\displaystyle f(x)=\frac{log_{10}(x)}{x};a=10,b=100$

373) $\displaystyle f(x)=\frac{log_2(x)}{x};a=32,b=64$

Answer:: $\displaystyle \frac{11}{2}ln2$

374) $\displaystyle f(x)=2^{−x};a=1,b=2$

375) $\displaystyle f(x)=2^{−x};a=3,b=4$

Answer:: $\displaystyle \frac{1}{ln(65,536)}$

376) Find the area under the graph of the function $\displaystyle f(x)=xe^{−x^2}$ between $\displaystyle x=0$ and $\displaystyle x=5$.

377) Compute the integral of $\displaystyle f(x)=xe^{−x^2}$ and find the smallest value of N such that the area under the graph $\displaystyle f(x)=xe^{−x^2}$ between $\displaystyle x=N$ and $\displaystyle x=N+10$ is, at most, 0.01.

Answer:: $\displaystyle ∫^{N+1}_Nxe^{−x^2}dx=\frac{1}{2}(e^{−N^2}−e^{−(N+1)^2}).$ The quantity is less than 0.01 when $\displaystyle N=2$.

378) Find the limit, as N tends to infinity, of the area under the graph of $\displaystyle f(x)=xe^{−x^2}$ between $\displaystyle x=0$ and $\displaystyle x=5$.

379) Show that $\displaystyle ∫^b_a\frac{dt}{t}=∫^{1/a}_{1/b}\frac{dt}{t}$ when $\displaystyle 0<a≤b$.

Answer:: $\displaystyle ∫^b_a\frac{dx}{x}=ln(b)−ln(a)=ln(\frac{1}{a})−ln(\frac{1}{b})=∫^{1/a}_{1/b}\frac{dx}{x}$

380) Suppose that $\displaystyle f(x)>0$ for all x and that f and g are differentiable. Use the identity $\displaystyle f^g=e^{glnf}$ and the chain rule to find the derivative of $\displaystyle f^g$.

381) Use the previous exercise to find the antiderivative of $\displaystyle h(x)=x^x(1+lnx)$ and evaluate $\displaystyle ∫^3_2x^x(1+lnx)dx$.

Answer:: 23

382) Show that if $\displaystyle c>0$, then the integral of $\displaystyle 1/x$ from ac to bc $\displaystyle (0<a<b)$ is the same as the integral of $\displaystyle 1/x$ from a to b.

The following exercises are intended to derive the fundamental properties of the natural log starting from the definition $\displaystyle ln(x)=∫^x_1\frac{dt}{t}$, using properties of the definite integral and making no further assumptions.

383) Use the identity $\displaystyle ln(x)=∫^x_1\frac{dt}{t}$ to derive the identity $\displaystyle ln(\frac{1}{x})=−lnx$.

Solution: We may assume that $\displaystyle x>1$,so $\displaystyle \frac{1}{x}<1.$ Then, $\displaystyle ∫^{1/x}_{1}\frac{dt}{t}$. Now make the substitution $\displaystyle u=\frac{1}{t}$, so $\displaystyle du=−\frac{dt}{t^2}$ and $\displaystyle \frac{du}{u}=−\frac{dt}{t}$, and change endpoints: $\displaystyle ∫^{1/x}_1\frac{dt}{t}=−∫^x_1\frac{du}{u}=−lnx.$

384) Use a change of variable in the integral $\displaystyle ∫^{xy}_1\frac{1}{t}dt$ to show that $\displaystyle lnxy=lnx+lny$ for $\displaystyle x,y>0$.

385) Use the identity $\displaystyle lnx=∫^x_1\frac{dt}{x}$ to show that $\displaystyle ln(x)$ is an increasing function of x on $\displaystyle [0,∞)$, and use the previous exercises to show that the range of $\displaystyle ln(x)$ is $\displaystyle (−∞,∞)$. Without any further assumptions, conclude that $\displaystyle ln(x)$ has an inverse function defined on $\displaystyle (−∞,∞).$

386) Pretend, for the moment, that we do not know that $\displaystyle e^x$ is the inverse function of $\displaystyle ln(x)$, but keep in mind that $\displaystyle ln(x)$ has an inverse function defined on $\displaystyle (−∞,∞)$. Call it E. Use the identity $\displaystyle lnxy=lnx+lny$ to deduce that $\displaystyle E(a+b)=E(a)E(b)$ for any real numbers a, b.

387) Pretend, for the moment, that we do not know that $\displaystyle e^x$ is the inverse function of $\displaystyle lnx$, but keep in mind that $\displaystyle lnx$ has an inverse function defined on $\displaystyle (−∞,∞)$. Call it E. Show that $\displaystyle E'(t)=E(t).$

Solution: $\displaystyle x=E(ln(x)).$ Then, $\displaystyle 1=\frac{E'(lnx)}{x}$ or $\displaystyle x=E'(lnx)$. Since any number t can be written $\displaystyle t=lnx$ for some x, and for such t we have $\displaystyle x=E(t)$, it follows that for any $\displaystyle t,E'(t)=E(t).$

388) The sine integral, defined as $\displaystyle S(x)=∫^x_0\frac{sint}{t}dt$ is an important quantity in engineering. Although it does not have a simple closed formula, it is possible to estimate its behavior for large x. Show that for $\displaystyle k≥1,|S(2πk)−S(2π(k+1))|≤\frac{1}{k(2k+1)π}.$ (Hint: $\displaystyle sin(t+π)=−sint$)

389) [T] The normal distribution in probability is given by $\displaystyle p(x)=\frac{1}{σ\sqrt{2π}}e^{−(x−μ)^2/2σ^2}$, where σ is the standard deviation and μ is the average. The standard normal distribution in probability, $\displaystyle p_s$, corresponds to $\displaystyle μ=0$ and $\displaystyle σ=1$. Compute the left endpoint estimates $\displaystyle R_{10}$ and $\displaystyle R_{100}$ of $\displaystyle ∫^1_{−1}\frac{1}{\sqrt{2π}}e^{−x^{2/2}}dx.$

Solution: $\displaystyle R_{10}=0.6811,R_{100}=0.6827$

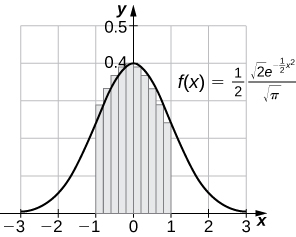
$CNX_Calc_Figure_05_06_202.jpeg$

390) [T] Compute the right endpoint estimates $\displaystyle R_{50}$ and $\displaystyle R_{100}$ of $\displaystyle ∫^5_{−3}\frac{1}{2\sqrt{2π}}e^{−(x−1)^2/8}$.