1.4: Graphs of Equations with Two Variables

Last updated
Save as PDF

Page ID: 35471

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Plot Points on a Rectangular Coordinate System

Just like maps use a grid system to identify locations, a grid system is used in algebra to show a relationship between two variables in a rectangular coordinate system. The rectangular coordinate system is also called the xy-plane or the “Cartesian coordinate plane” (after the French mathematician Rene Descartes).

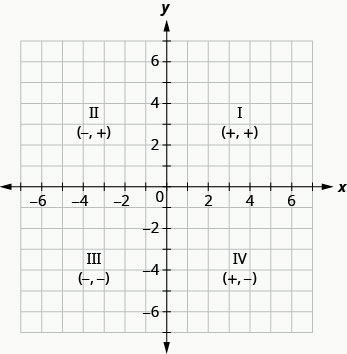
The rectangular coordinate system is formed by two intersecting number lines, one horizontal and one vertical. The horizontal number line is called the $x$-axis. The vertical number line is called the $y$-axis. These axes divide a plane into four regions, called quadrants. The quadrants are identified by Roman numerals, beginning on the upper right and proceeding counterclockwise. See Figure $\PageIndex{1}$. Any point in the plane can be located by indicating a position on the horizontal number line and a position on the vertical number line.

This figure shows a square grid. A horizontal number line in the middle is labeled x. A vertical number line in the middle is labeled y. The number lines intersect at zero and together divide the square grid into 4 equally sized smaller squares. The square in the top right is labeled I. The square in the top left is labeled II. The square in the bottom left is labeled III. The square in the bottom right is labeled IV. — Figure $\PageIndex{1}$

In the rectangular coordinate system, every point is represented by an ordered pair. The first number in the ordered pair is the $x$-coordinate of the point, representing its horizontal position, and the second number is the $y$-coordinate of the point, representing its vertical position. The phrase “ordered pair” means that the order is important.

ORDERED PAIR

An ordered pair $(x,y)$ gives the coordinates of a point in a rectangular coordinate system. The first number is the $x$-coordinate. The second number is the $y$-coordinate.

$This figure shows the expression (x, y). The variable x is labeled x-coordinate. The variable y is labeled y-coordinate.$

What is the ordered pair of the point where the axes cross? At that point both coordinates are zero, so its ordered pair is $(0,0)$.The point $(0,0)$ has a special name. It is called the origin.

THE ORIGIN

The point $(0,0)$ is called the origin. It is the point where the $x$-axis and $y$-axis intersect.

We use the coordinates to locate a point on the xy-plane. Let’s plot the point $(1,3)$ as an example. First, locate 1 on the x-axis and lightly sketch a vertical line through $x=1$. Then, locate 3 on the y-axis and sketch a horizontal line through y=3.y=3. Now, find the point where these two lines meet—that is the point with coordinates $(1,3)$. See Figure.

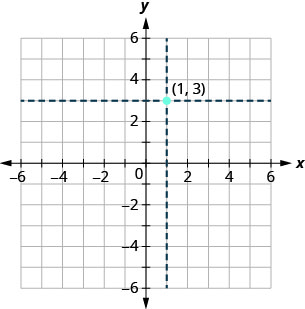
This figure shows a point plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point (1, 3) is labeled. A dashed vertical line goes through the point and intersects the x-axis at xplus1. A dashed horizontal line goes through the point and intersects the y-axis at yplus3. — Figure $\PageIndex{2}$

Notice that the vertical line through $x=1$ and the horizontal line through $y=3$ are not part of the graph. We just used them to help us locate the point $(1,3)$.

When one of the coordinate is zero, the point lies on one of the axes. In Figure the point $(0,4)$ is on the y-axis and the point $(−2,0)$ is on the x-axis.

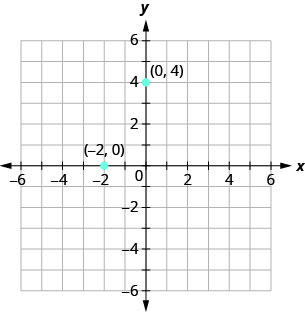
This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point (negative 2, 0) is labeled and lies on the x-axis. The point (0, 4) is labeled and lies on the y-axis.

POINTS ON THE AXES

Points with a y-coordinate equal to 0 are on the x-axis, and have coordinates $(a,0)$.

Points with an x-coordinate equal to 0 are on the y-axis, and have coordinates $(0,b)$.

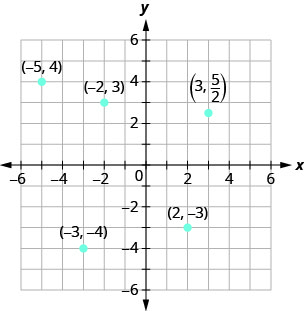
Example $\PageIndex{1}$

Plot each point in the rectangular coordinate system and identify the quadrant in which the point is located:

ⓐ $(−5,4$) ⓑ $(−3,−4)$ ⓒ $(2,−3)$ ⓓ $(0,−1)$ ⓔ $(3,\dfrac{5}{2})$.

Answer

The first number of the coordinate pair is the x-coordinate, and the second number is the y-coordinate. To plot each point, sketch a vertical line through the x-coordinate and a horizontal line through the y-coordinate. Their intersection is the point.

ⓐ Since $x=−5$, the point is to the left of the y-axis. Also, since $y=4$, the point is above the x-axis. The point $(−5,4)$ is in Quadrant II.

ⓑ Since $x=−3$, the point is to the left of the y-axis. Also, since $y=−4$, the point is below the x-axis. The point $(−3,−4)$ is in Quadrant III.

ⓓ Since $x=0$, the point whose coordinates are $(0,−1)$ is on the y-axis.

ⓔ Since $x=3$, the point is to the right of the y-axis. Since $y=\dfrac{5}{2})$, the point is above the x-axis. (It may be helpful to write $\dfrac{5}{2})$ as a mixed number or decimal.) The point $(3,\dfrac{5}{2})$ is in Quadrant I.

$This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The following points are labeled: (3, 5 divided by 2), (negative 2, 3), negative 5, 4), (negative 3, negative 4), and (2, negative 3).$

Example $\PageIndex{2}$

Plot each point in a rectangular coordinate system and identify the quadrant in which the point is located:

ⓐ $(−2,1)$ ⓑ $(−3,−1)$ ⓒ $(4,−4)$ ⓓ $(−4,4)$ ⓔ $(−4,\dfrac{3}{2})$

Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point labeled a is 2 units to the left of the origin and 1 unit above the origin and is located in quadrant II. The point labeled b is 3 units to the left of the origin and 1 unit below the origin and is located in quadrant III. The point labeled c is 4 units to the right of the origin and 4 units below the origin and is located in quadrant IV. The point labeled d is 4 units to the left of the origin and 4 units above the origin and is located in quadrant II. The point labeled e is 4 units to the left of the origin and 1 and a half units above the origin and is located in quadrant II.$

Example $\PageIndex{3}$

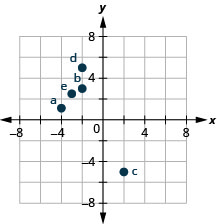
Plot each point in a rectangular coordinate system and identify the quadrant in which the point is located:

Answer: $This figure shows points plotted on the x y-coordinate plane. The x and y axes run from negative 6 to 6. The point labeled a is 4 units to the left of the origin and 1 unit above the origin and is located in quadrant II. The point labeled b is 2 units to the left of the origin and 3 units above the origin and is located in quadrant II. The point labeled c is 2 units to the right of the origin and 5 units below the origin and is located in quadrant IV. The point labeled d is 2 units to the left of the origin and 5 units above the origin and is located in quadrant II. The point labeled e is 3 units to the left of the origin and 2 and a half units above the origin and is located in quadrant II.$

The signs of the x-coordinate and y-coordinate affect the location of the points. You may have noticed some patterns as you graphed the points in the previous example. We can summarize sign patterns of the quadrants in this way:

QUADRANTS

Quadrant I	Quadrant II	Quadrant III	Quadrant IV
$(x,y)$	$(x,y)$	$(x,y)$	$(x,y)$
$(+,+)$	$(−,+)$	$(−,−)$	$(+,−)$

$This figure shows the x y-coordinate plane with the four quadrants labeled. In the top right of the plane is quadrant I labeled (plus, plus). In the top left of the plane is quadrant II labeled (minus, plus). In the bottom left of the plane is quadrant III labeled (minus, minus). In the bottom right of the plane is quadrant IV labeled (plus, minus).$

Solution Set for an Equation with Two Variables

Equations with two variables (often the variables are names $x$ and $y$) usually have infinitely many solutions. For every number that is substituted for one variable $x$ we can look for corresponding $y$-values that make the equation true. If we find one, this pair of values is a solution to the equation and it can be represented by the ordered pair $(x,y)$. When we substitute these values of x and y into the equation, the result is a true statement, because the value on the left side is equal to the value on the right side.

SOLUTION OF A LINEAR EQUATION IN TWO VARIABLES

An ordered pair $(x,y)$ is a solution of an equation if the equation is a true statement when the $x$- and $y$-values of the ordered pair are substituted into the equation.

The solution set for an equation with two variables is the set of all ordered pairs that make the equation true. We can plot solutions in the rectangular coordinate system. A graph of an equation is a visual representation of all the solutions of the equation. It is an example of the saying, “A picture is worth a thousand words.” Every point on the graph is a solution of the equation. And, every solution of this equation is on the graph. Points not on the graph are not solutions!

GRAPH OF An EQUATION

The graph of an equation in two variables is the set of all ordered pair solutions to that equation, plotted in the rectangular coordinate system.

Every point on the graph is a solution of the equation.
Every solution of this equation is a point on this graph.

Quadrant I	Quadrant II	Quadrant III	Quadrant IV
\((x,y)\)	\((x,y)\)	\((x,y)\)	\((x,y)\)
\((+,+)\)	\((−,+)\)	\((−,−)\)	\((+,−)\)