6.4E: Exercises

Last updated

Jan 20, 2020
Save as PDF
- 6.4: The Other Trigonometric Functions
- 6.5: Right Triangle Trigonometry

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

5.3: The Other Trigonometric Functions

Verbal

1) On an interval of $[ 0,2π )$ , can the sine and cosine values of a radian measure ever be equal? If so, where?

Answer: Yes, when the reference angle is $\dfrac{π}{4}$ and the terminal side of the angle is in quadrants I and III. Thus, at $x=\dfrac{π}{4},\dfrac{5π}{4}$ , the sine and cosine values are equal.

2) What would you estimate the cosine of $\pi$ degrees to be? Explain your reasoning.

3) For any angle in quadrant II, if you knew the sine of the angle, how could you determine the cosine of the angle?

Answer: Substitute the sine of the angle in for $y$ in the Pythagorean Theorem $x^2+y^2=1$ . Solve for $x$ and take the negative solution.

4) Describe the secant function.

5) Tangent and cotangent have a period of $π$ . What does this tell us about the output of these functions?

Answer: The outputs of tangent and cotangent will repeat every $π$ units.

Algebraic

For the exercises 6-17, find the exact value of each expression.

6) $\tan \dfrac{π}{6}$

7) $\sec \dfrac{π}{6}$

Answer: $\dfrac{2\sqrt{3}}{3}$

8) $\csc \dfrac{π}{6}$

9) $\cot \dfrac{π}{6}$

Answer: $\sqrt{3}$

10) $\tan \dfrac{π}{4}$

11) $\sec \dfrac{π}{4}$

Answer: $\sqrt{2}$

12) $\csc \dfrac{π}{4}$

13) $\cot \dfrac{π}{4}$

Answer: $1$

14) $\tan \dfrac{π}{3}$

15) $\sec \dfrac{π}{3}$

Answer: $2$

16) $\csc \dfrac{π}{3}$

17) $\cot \dfrac{π}{3}$

Answer: $\dfrac{\sqrt{3}}{3}$

For the exercises 18-48, use reference angles to evaluate the expression.

18) $\tan \dfrac{5π}{6}$

19) $\sec \dfrac{7π}{6}$

Answer: $−\dfrac{2\sqrt{3}}{3}$

20) $\csc \dfrac{11π}{6}$

21) $\cot \dfrac{13π}{6}$

Answer: $\sqrt{3}$

22) $\tan \dfrac{7π}{4}$

23) $\sec \dfrac{3π}{4}$

Answer: $−\sqrt{2}$

24) $\csc \dfrac{5π}{4}$

25) $\cot \dfrac{11π}{4}$

Answer: $−1$

26) $\tan \dfrac{8π}{3}$

27) $\sec \dfrac{4π}{3}$

Answer: $−2$

28) $\csc \dfrac{2π}{3}$

29) $\cot \dfrac{5π}{3}$

Answer: $−\dfrac{\sqrt{3}}{3}$

30) $\tan 225°$

31) $\sec 300°$

Answer: $2$

32) $\csc 150°$

33) $\cot 240°$

Answer: $\dfrac{\sqrt{3}}{3}$

34) $\tan 330°$

35) $\sec 120°$

Answer: $−2$

36) $\csc 210°$

37) $\cot 315°$

Answer: $−1$

38) If $\sin t= \dfrac{3}{4}$ , and $t$ is in quadrant II, find $\cos t, \sec t, \csc t, \tan t, \cot t$ .

39) If $\cos t=−\dfrac{1}{3},$ and $t$ is in quadrant III, find $\sin t, \sec t, \csc t, \tan t, \cot t$ .

Answer: If $\sin t=−\dfrac{2\sqrt{2}}{3}, \sec t=−3, \csc t=−\csc t=−\dfrac{3\sqrt{2}}{4},\tan t=2\sqrt{2}, \cot t= \dfrac{\sqrt{2}}{4}$

40) If $\tan t=\dfrac{12}{5},$ and $0≤t< \dfrac{π}{2}$ , find $\sin t, \cos t, \sec t, \csc t,$ and $\cot t$ .

41) If $\sin t= \dfrac{\sqrt{3}}{2}$ and $\cos t=\dfrac{1}{2},$ find $\sec t, \csc t, \tan t,$ and $\cot t$ .

Answer: $\sec t=2, \csc t=\csc t=\dfrac{2\sqrt{3}}{3}, \tan t= \sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}$

42) If $\sin 40°≈0.643 \; \cos 40°≈0.766 \; \sec 40°,\csc 40°,\tan 40°, \text{ and } \cot 40°$ .

43) If $\sin t= \dfrac{\sqrt{2}}{2},$ what is the $\sin (−t)$ ?

Answer: $−\dfrac{\sqrt{2}}{2}$

44) If $\cos t= \dfrac{1}{2},$ what is the $\cos (−t)$ ?

45) If $\sec t=3.1,$ what is the $\sec (−t)$ ?

Answer: $3.1$

46) If $\csc t=0.34,$ what is the $\csc (−t)$ ?

47) If $\tan t=−1.4,$ what is the $\tan (−t)$ ?

Answer: $1.4$

48) If $\cot t=9.23,$ what is the $\cot (−t)$ ?

Graphical

For the exercises 49-51, use the angle in the unit circle to find the value of the each of the six trigonometric functions.

49)

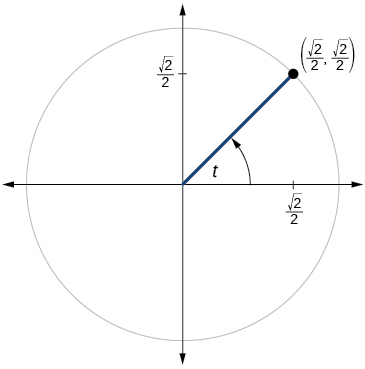
$CNX_Precalc_Figure_05_03_201.jpg$

Answer: $\sin t= \dfrac{\sqrt{2}}{2}, \cos t= \dfrac{\sqrt{2}}{2}, \tan t=1,\cot t=1,\sec t= \sqrt{2}, \csc t= \csc t= \sqrt{2}$

50)

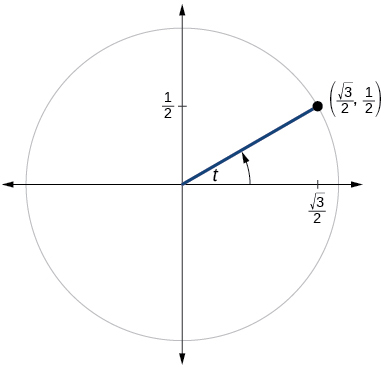
$CNX_Precalc_Figure_05_03_202.jpg$

51)

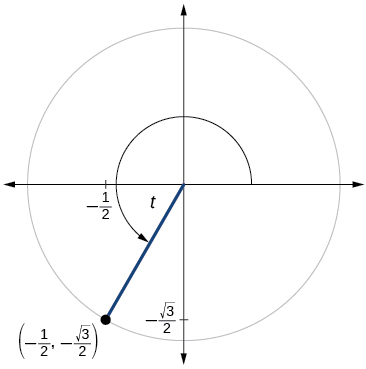
$CNX_Precalc_Figure_05_03_203.jpg$

Answer: $\sin t=−\dfrac{\sqrt{3}}{2}, \cos t=−\dfrac{1}{2}, \tan t=\sqrt{3}, \cot t= \dfrac{\sqrt{3}}{3}, \sec t=−2, \csc t=−\csc t=−\dfrac{2\sqrt{3}}{3}$

Technology

For the exercises 52-61, use a graphing calculator to evaluate.

52) $\csc \dfrac{5π}{9}$

53) $\cot \dfrac{4π}{7}$

Answer: $–0.228$

54) $\sec \dfrac{π}{10}$

55) $\tan \dfrac{5π}{8}$

Answer: $–2.414$

56) $\sec \dfrac{3π}{4}$

57) $\csc \dfrac{π}{4}$

Answer: $1.414$

58) $\tan 98°$

59) $\cot 33°$

Answer: $1.540$

60) $\cot 140°$

61) $\sec 310°$

Answer: $1.556$

Extensions

For the exercises 62-69, use identities to evaluate the expression.

62) If $\tan (t)≈2.7,$ and $\sin (t)≈0.94,$ find $\cos (t)$ .

63) If $\tan (t)≈1.3,$ and $\cos (t)≈0.61$ , find $\sin (t)$ .

Answer: $\sin (t)≈0.79$

64) If $\csc (t)≈3.2,$ and $\csc (t)≈3.2,$ and $\cos (t)≈0.95,$ find $\tan (t)$ .

65) If $\cot (t)≈0.58,$ and $\cos (t)≈0.5,$ find $\csc (t)$ .

Answer: $\csc (t)≈1.16$

66) Determine whether the function $f(x)=2 \sin x \cos x$ is even, odd, or neither.

67) Determine whether the function $f(x)=3 \sin ^2 x \cos x + \sec x$ is even, odd, or neither.

Answer: even

68) Determine whether the function $f(x)= \sin x −2 \cos ^2 x$ is even, odd, or neither.

69) Determine whether the function $f(x)= \csc ^2 x+ \sec x$ is even, odd, or neither.

Answer: even

For the exercises 70-71, use identities to simplify the expression.

70) $\csc t \tan t$

71) $\dfrac{\sec t}{ \csc t}$

Answer: $\dfrac{ \sin t}{ \cos t}= \tan t$

Real-World Applications

72) The amount of sunlight in a certain city can be modeled by the function $h=15 \cos \left(\dfrac{1}{600}d\right),$ where $h$ represents the hours of sunlight, and $d$ is the day of the year. Use the equation to find how many hours of sunlight there are on February 10, the $42^{nd}$ day of the year. State the period of the function.

73) The amount of sunlight in a certain city can be modeled by the function $h=16 \cos \left(\dfrac{1}{500}d\right)$ , where $h$ represents the hours of sunlight, and $d$ is the day of the year. Use the equation to find how many hours of sunlight there are on September 24, the $267^{th}$ day of the year. State the period of the function.

Answer: $13.77$ hours, period: $1000π$

74) The equation $P=20 \sin (2πt)+100$ models the blood pressure, $P$ , where $t$ represents time in seconds.

Find the blood pressure after $15$ seconds.
What are the maximum and minimum blood pressures?

75) The height of a piston, $h$ , in inches, can be modeled by the equation $y=2 \cos x+6,$ where $x$ represents the crank angle. Find the height of the piston when the crank angle is $55°$ .

Answer: $7.73$ inches

76) The height of a piston, $h$ ,in inches, can be modeled by the equation $y=2 \cos x+5,$ where $x$ represents the crank angle. Find the height of the piston when the crank angle is $55°$ .

Search

Text Color

Text Size

Margin Size

Font Type