Section 6.5E: Exercises

Last updated

Jan 20, 2020
Save as PDF
- 6.5: Right Triangle Trigonometry
- Chapter 7: Periodic Functions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

5.4: Right Triangle Trigonometry

Verbal

1) For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.

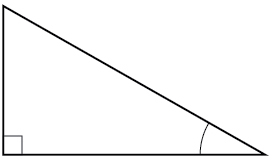
$CNX_Precalc_Figure_05_04_201.jpg$

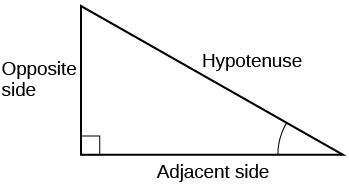
Answer: $CNX_Precalc_Figure_05_04_202.jpg$

2) When a right triangle with a hypotenuse of $1$ is placed in the unit circle, which sides of the triangle correspond to the $x$ - and $y$ -coordinates?

3) The tangent of an angle compares which sides of the right triangle?

Answer: The tangent of an angle is the ratio of the opposite side to the adjacent side.

4) What is the relationship between the two acute angles in a right triangle?

5) Explain the cofunction identity.

Answer: For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.

Algebraic

For the exercises 6-9, use cofunctions of complementary angles.

6) $\cos (34°)= \sin (\_\_°)$

7) $\cos (\dfrac{π}{3})= \sin (\_\_\_)$

Answer: $\dfrac{π}{6}$

8) $\csc (21°) = \sec (\_\_\_°)$

9) $\tan (\dfrac{π}{4})= \cot (\_\_)$

Answer: $\dfrac{π}{4}$

For the exercises 10-16, find the lengths of the missing sides if side $a$ is opposite angle $A$ , side $b$ is opposite angle $B$ , and side $c$ is the hypotenuse.

10) $\cos B= \dfrac{4}{5},a=10$

11) $\sin B= \dfrac{1}{2}, a=20$

Answer: $b= \dfrac{20\sqrt{3}}{3},c= \dfrac{40\sqrt{3}}{3}$

12) $\tan A= \dfrac{5}{12},b=6$

13) $\tan A=100,b=100$

Answer: $a=10,000,c=10,000.5$

14) $\sin B=\dfrac{1}{\sqrt{3}}, a=2$

15) $a=5, ∡ A=60^∘$

Answer: $b=\dfrac{5\sqrt{3}}{3},c=\dfrac{10\sqrt{3}}{3}$

16) $c=12, ∡ A=45^∘$

Graphical

For the exercises 17-22, use Figure below to evaluate each trigonometric function of angle $A$ .

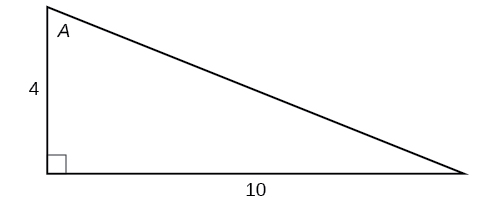
$CNX_Precalc_Figure_05_04_203.jpg$

17) $\sin A$

Answer: $\dfrac{5\sqrt{29}}{29}$

18) $\cos A$

19) $\tan A$

Answer: $\dfrac{5}{2}$

20) $\csc A$

21) $\sec A$

Answer: $\dfrac{\sqrt{29}}{2}$

22) $\cot A$

For the exercises 23-,28 use Figure below to evaluate each trigonometric function of angle $A$ .

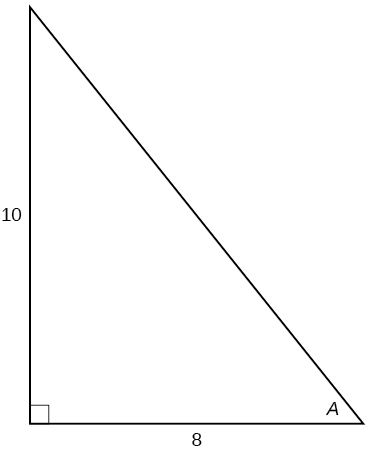
$CNX_Precalc_Figure_05_04_204.jpg$

23) $\sin A$

Answer: $\dfrac{5\sqrt{41}}{41}$

24) $\cos A$

25) $\tan A$

Answer: $\dfrac{5}{4}$

26) $\csc A$

27) $\sec A$

Answer: $\dfrac{\sqrt{41}}{4}$

28) $\cot A$

For the exercises 29-31, solve for the unknown sides of the given triangle.

29)

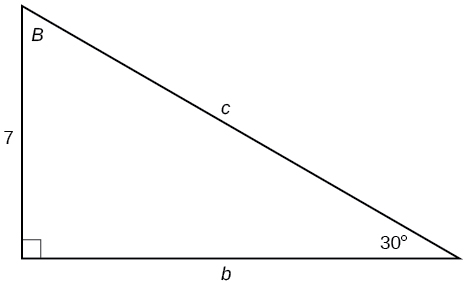
$CNX_Precalc_Figure_05_04_205.jpg$

Answer: $c=14, b=7\sqrt{3}$

30)

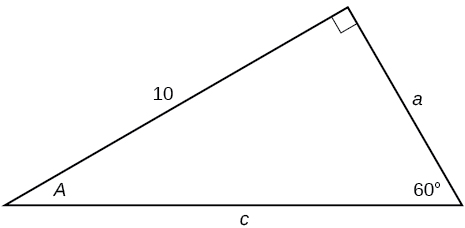
$CNX_Precalc_Figure_05_04_206.jpg$

31)

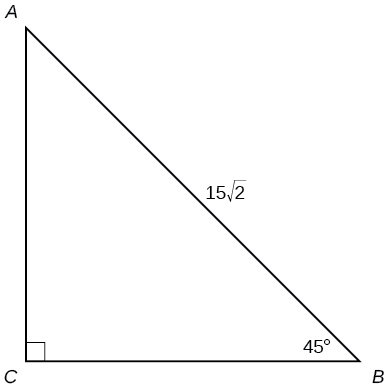
$CNX_Precalc_Figure_05_04_207.jpg$

Answer: $a=15, b=15$

Technology

For the exercises 32-41, use a calculator to find the length of each side to four decimal places.

32)

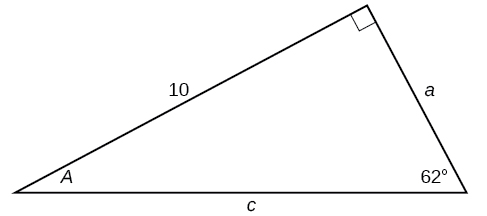
$CNX_Precalc_Figure_05_04_208.jpg$

33)

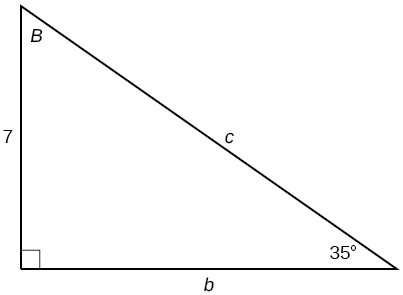
$CNX_Precalc_Figure_05_04_209.jpg$

Answer: $b=9.9970, c=12.2041$

34)

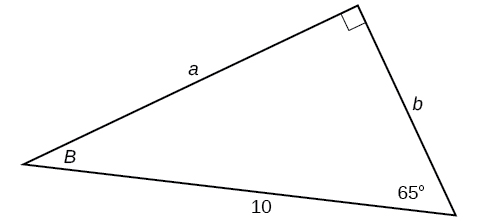
$CNX_Precalc_Figure_05_04_210.jpg$

35)

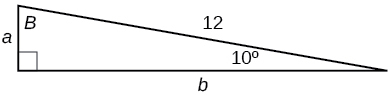
$CNX_Precalc_Figure_05_04_211.jpg$

Answer: $a=2.0838, b=11.8177$

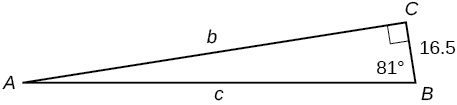
36)

$CNX_Precalc_Figure_05_04_212.jpg$

37) $b=15, ∡B=15^∘$

Answer: $a=55.9808,c=57.9555$

38) $c=200, ∡B=5^∘$

39) $c=50, ∡B=21^∘$

Answer: $a=46.6790,b=17.9184$

40) $a=30, ∡A=27^∘$

41) $b=3.5, ∡A=78^∘$

Answer: $a=16.4662,c=16.8341$

Extensions

42) Find $x$ .

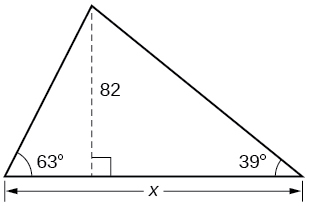
$CNX_Precalc_Figure_05_04_213.jpg$

43) Find $x$ .

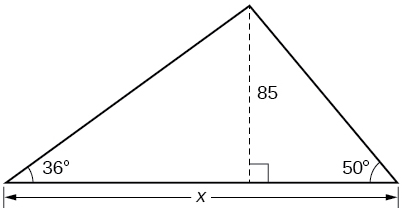
$CNX_Precalc_Figure_05_04_214.jpg$

Answer: $188.3159$

44) Find $x$ .

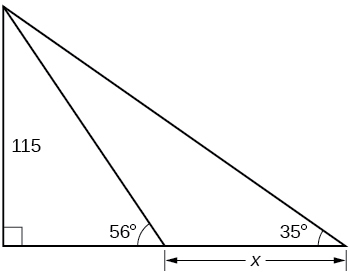
$CNX_Precalc_Figure_05_04_215.jpg$

45) Find $x$ .

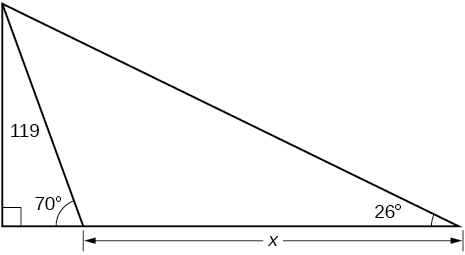
$CNX_Precalc_Figure_05_04_216.jpg$

Answer: $200.6737$

46) A radio tower is located $400$ feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $36°$ , and that the angle of depression to the bottom of the tower is $23°$ . How tall is the tower?

47) A radio tower is located $325$ feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is $43°$ , and that the angle of depression to the bottom of the tower is $31°$ . How tall is the tower?

Answer: $498.3471$ ft

48) A $200$ -foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $15°$ , and that the angle of depression to the bottom of the tower is $2°$ . How far is the person from the monument?

49) A $400$ -foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is $18°$ , and that the angle of depression to the bottom of the monument is $3°$ . How far is the person from the monument?

Answer: $1060.09$ ft

50) There is an antenna on the top of a building. From a location $300$ feet from the base of the building, the angle of elevation to the top of the building is measured to be $40°$ . From the same location, the angle of elevation to the top of the antenna is measured to be $43°$ . Find the height of the antenna.

51) There is lightning rod on the top of a building. From a location $500$ feet from the base of the building, the angle of elevation to the top of the building is measured to be $36°$ . From the same location, the angle of elevation to the top of the lightning rod is measured to be $38°$ . Find the height of the lightning rod.

Answer: $27.372$ ft

Real-World Applications

52) A $33$ -ft ladder leans against a building so that the angle between the ground and the ladder is $80°$ . How high does the ladder reach up the side of the building?

53) A $23$ -ft ladder leans against a building so that the angle between the ground and the ladder is $80°$ . How high does the ladder reach up the side of the building?

Answer: $22.6506$ ft

54) The angle of elevation to the top of a building in New York is found to be $9$ degrees from the ground at a distance of $1$ mile from the base of the building. Using this information, find the height of the building.

55) The angle of elevation to the top of a building in Seattle is found to be $2$ degrees from the ground at a distance of $2$ miles from the base of the building. Using this information, find the height of the building.

Answer: $368.7633$ ft

56) Assuming that a $370$ -foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be $60°$ , how far from the base of the tree am I?

Contributor

Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

Search

Text Color

Text Size

Margin Size

Font Type