0.2: Sets of Numbers
- Page ID
- 35146
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One of the basic tools of higher mathematics is the concept of sets. A set of numbers is a collection of numbers, called elements. The set can be either a finite collection or an infinite collection of numbers. One way of denoting a set, called roster notation, is to use "\(\{\)" and "\(\}\)", with the elements separated by commas; for instance, the set \(\{2, 31 \}\) contains the elements 2 and 31.
In set notation, there is a symbol "\(\cup\)" to represent “or,” and we say we are taking the union of the two sets. For example, we can take the union of the sets\(\{2,3,5\}\) and \(\{4,5,6\}\): \(\{2,3,5\} \cup \{4,6\} = \{2,3,4,5,6\}\). It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set.
Natural Numbers and Whole Numbers
When a set contains an infinite number of elements, it is impossible to list all of them, so we need ways to indicate which numbers are included. Some infinite sets are very well-known, and form the basis of our number system. These are the numbers we use to count objects in our world: \(1, 2, 3, 4\), and so on. They are called the counting numbers, or natural numbers and they are so important that they are designated by the special symbol \(\mathbb{N}\). If we add zero to the counting numbers, we get the set of whole numbers.
- Counting Numbers: \(\mathbb{N} = \{1, 2, 3, …\}\)
- Whole Numbers: \(\{0, 1, 2, 3, …\}\)
The notation “\(…\)” is called an ellipsis and means “and so on,” or that the pattern continues endlessly. Note that all of the natural numbers are included in the set of whole numbers. We say that the natural numbers are a subset of the whole numbers.
Integers
A negative number is a number less than 0. The negative numbers are to the left of zero on the number line (Figure \(\PageIndex{1}\)).
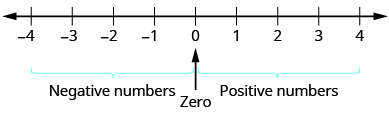
Figure \(\PageIndex{1}\). The number line shows the location of positive and negative numbers.
You may have noticed that, on the number line, the negative numbers are a mirror image of the positive numbers, with zero in the middle. Because the numbers \(2\) and \(−2\) are the same distance from zero, each one is called the opposite of the other. The opposite of \(2\) is \(−2\), and the opposite of \(−2\) is \(2\).
Definition: OPPOSITE
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
Figure \(\PageIndex{2}\) illustrates the definition.

Figure \(\PageIndex{2}\). The opposite of 3 is \(−3\).
OPPOSITE NOTATION
\[ -a \text{ means the opposite of the number }a \\ \text{The notation } -a \text{ is read as “the opposite of }a \text{.”} \nonumber\]
The set of whole numbers together with their opposites is called the integers. (Thus, the whole numbers are a subset of the integers.) The integers are also very important, and are given the special designation \(\mathbb{Z}\).
- Integers: \(\mathbb{Z} = \{… ,−3,−2,−1,0,1,2,3, …\}\)
Rational, Irrational, and Real Numbers
We often see only the integers marked on the number line, which may cause us to forget (temporarily) that there are many numbers in between every pair of integers; in fact, there are an infinite amount of numbers in between every pair of integers! The next set we consider is the set of rational numbers, designated by \(\mathbb{Q}\). You have worked with rational numbers before, but we will give a careful definition of \(\mathbb{Q}\). (Using this definition, it can be seen that the set of integers is a subset of the rational numbers.)
Definition: Rational Numbers
A rational number is a number that can be expressed as a ratio of two integers (with the second integer not equal to zero). Hence, a rational number can be written as \(\frac{m}{n}\) for some integers \(m\) and \(n\), where \(n\neq 0\). The set of rational numbers is denoted as \(\mathbb{Q}\).
Any decimal that terminates, or ends after a number of digits (such as 7.3 or −1.2684), can be written as a ratio of two integers, and thus is a rational number. We can use the place value of the last digit as the denominator when writing the decimal as a fraction. For example, -1.2684 can be written as \(\frac{-12684}{10000}\). Also, any rational number can be written in decimal form where the decimal terminates or begins to repeat its digits in the same pattern, infinitely. The decimal for \(\frac{1}{3}\) is the number \(0.\overline{3}\). The bar over the 3 indicates that the number 3 repeats infinitely. The number(s) under the bar is called the repeating block and it repeats itself forever.
Every rational number can be written both as a ratio of integers and as a decimal that terminates or begins to repeat.
It may seem strange to you, as it seemed not only strange, but impossible to early mathematicians 6,000 years or so ago; but it turns out that there are numbers on the number line that cannot be expressed as a ratio of two integers. These numbers are called irrational numbers. When we include the irrational numbers along with the rational numbers, we get the set of numbers called the real numbers, denoted \(\mathbb{R}\). Some famous irrational numbers that you may be familiar with are: \(\pi\) and \(\sqrt{2}\).
Definition: Irrational Numbers
An irrational number is a real number that can not be expressed as a ratio of two integers; i.e., is not rational.
Definition: Real Numbers
The real numbers , denoted \(\mathbb{R}\), are the numbers corresponding to all the points on the number line.
Later in this course we will introduce numbers beyond the real numbers. Figure \(\PageIndex{3}\) illustrates how the number sets we’ve used so far fit together.
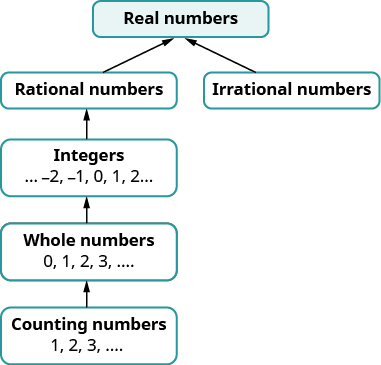
Figure \(\PageIndex{3}\). This chart shows the number sets that make up the set of real numbers.
Example \(\PageIndex{1}\)
Given the set \(\{−7,\,\frac{14}{5},\,8,\,\sqrt{5},\,5.9,\,−\sqrt{64}\}\), list the a) whole numbers b) integers c) rational numbers d) irrational numbers e) real numbers.
Solution
a) Remember, the whole numbers are \(\{0,1,2,3,…\}\) so 8 is the only whole number given.
b) The integers are the whole numbers and their opposites (which includes 0). So the whole number 8 is an integer, and −7 is the opposite of a whole number so it is an integer, too. Also, notice that 64 is the square of 8 so \(−\sqrt{64}=−8\). T\,he integers are \(−7,\,8,\) and \(−\sqrt{64}\).
c) Since all integers are rational, then \(−7,\,8,\) and \(−\sqrt{64}\) are rational. Rational numbers also include fractions and decimals that repeat or stop, so \(\frac{14}{5}\) and \(5.9\) are rational. The list of rational numbers is \(−7,\,\frac{14}{5},\,8,\,5.9,\) and \(−\sqrt{64}\).
d) Remember that 5 is not a perfect square, so \(\sqrt{5}\) is irrational.
e) All the numbers listed are real numbers.
![]() \(\PageIndex{1}\)
\(\PageIndex{1}\)
Given the set \(\{−3,\,−\sqrt{2},\,0.\overline{3},\,\frac{9}{5},\,4,\sqrt{49}\},\) list the a) whole numbers b) integers c) rational numbers d) irrational numbers e) real numbers.
- Answer
-
a) \(4,\sqrt{49}\) \, b) \(−3,4,\sqrt{49}\) \, c) \(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) \, d) \(−\sqrt{2}\) \, e) \(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
![]() \(\PageIndex{2}\)
\(\PageIndex{2}\)
Given numbers \(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) list the a) whole numbers b) integers c) rational numbers d) irrational numbers e) real numbers.
- Answer
-
a) \(6,\sqrt{121}\)
b) \(−\sqrt{25},−1,6,\sqrt{121}\)
c) \(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
d) \(2.041975...\)
e) \(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
Locate Fractions and Decimals on the Number Line
We now want to include fractions and decimals on the number line. Let’s start with fractions and locate \(\frac{1}{5},\,−\frac{4}{5},\,3,\, \frac{7}{4},\, −\frac{9}{2},\, −5\) and \(\frac{8}{3}\) on the number line.
We’ll start with the whole numbers 3 and −5 because they are the easiest to plot. See Figure \(\PageIndex{4}\).
The proper fractions listed are \(\frac{1}{5}\) and \(−\frac{4}{5}.\) We know the proper fraction \(\frac{1}{5}\) has value less than one and so would be located between 0 and 1. The denominator is 5, so we divide the unit from 0 to 1 into 5 equal parts \(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). We plot \(\frac{1}{5}\).
Similarly, \(−\frac{4}{5}\) is between 0 and −1. After dividing the unit into 5 equal parts we plot \(−\frac{4}{5}\).
Finally, look at the improper fractions \(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Locating these points may be easier if you change each of them to a decimal (see Example \(\PageIndex{3}\) below).
\[\dfrac{7}{4}=1.75 \qquad −\dfrac{9}{2}=−4.5 \qquad \dfrac{8}{3}=2.\overline{6}\nonumber\]
Figure \(\PageIndex{4}\) shows the number line with all the points plotted.

Example \(\PageIndex{2}\)
Locate and label the following on a number line: \(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) and \(\frac{7}{3}\).
Solution
Locate and plot the integers, \(4,−3.\)
Locate the proper fraction \(\frac{3}{4}\) first. The fraction \(\frac{3}{4}\) is between 0 and 1. Divide the distance between 0 and 1 into four equal parts, then we plot \(\frac{3}{4}\). Similarly plot \(−\frac{1}{4}\).
Now locate the improper fractions \(\frac{6}{5},−\frac{5}{2},\) and \(\frac{7}{3}\). It is easier to plot them if we convert them to decimals and then plot them as described above: \(\frac{6}{5}=1.2,\quad −\frac{5}{2}=−2.5,\quad \frac{7}{3}=2.\overline{3}\).

![]() \(\PageIndex{3}\)
\(\PageIndex{3}\)
Locate and label the following on a number line: \(−1,\quad \frac{1}{3},\quad \frac{6}{5},\quad −\frac{7}{4},\quad \frac{9}{2},\quad 5,\quad −\frac{8}{3}\).
- Answer
-
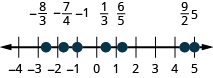
![]() \(\PageIndex{4}\)
\(\PageIndex{4}\)
Locate and label the following on a number line: \(−2,\quad \frac{2}{3},\quad \frac{7}{5},\quad −\frac{7}{4},\quad \frac{7}{2},\quad 3,\quad −\frac{7}{3}\).
- Answer
-
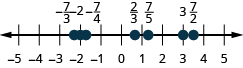
Example \(\PageIndex{3}\)
Since decimals are forms of fractions, locating decimals on the number line is similar to locating fractions on the number line.
Locate on the number line: a) 0.4; b) −0.74.
Solution
a) The decimal number 0.4 is equivalent to \(\frac{4}{10}\), a proper fraction, so 0.4 is located between 0 and 1. On a number line, divide the interval between 0 and 1 into 10 equal parts. Now label the parts 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. We write 0 as 0.0 and 1 as 1.0, so that the numbers are consistently in tenths. Finally, mark 0.4 on the number line.

b) The decimal \(−0.74\) is equivalent to \(−\frac{74}{100}\), so it is located between 0 and .−1. On a number line, mark off and label the hundredths in the interval between 0 and −1.

![]() \(\PageIndex{5}\)
\(\PageIndex{5}\)
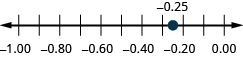
Locate on the number line: a) \(0.6\); b) \(−0.25.\)
- Answer
-
a)

b)
Interval Notation and Set-builder Notation
In calculus, sets of real numbers that span a given interval on the number line are often important. A special notation called interval notation is often used, in which only the beginning number and end number of the interval are named, and it is understood that all numbers in between them are included in the set. The braces that are used for roster notation are not used in interval notation; rather, we use a square bracket "[" when the set includes the endpoint and a parenthesis "(" to indicate that the endpoint is either not included or the interval is unbounded. For example, we express the set of real numbers that are greater than 3 as \((3,\infty)\). There is no upper end to this set; the interval is unbounded. The symbol \(\infty\) is read as “infinity.” It is not an actual number.
Conventions for sets written using interval notation
- The smallest term from the interval is written first.
- The largest term in the interval is written second, following a comma.
- All real numbers between the smallest and largest term are included in the set.
- Parentheses, "\((\)" or "\()\)," are used to signify that an endpoint is not included, called exclusive.
- Brackets, "\([\)" or "\(]\)," are used to indicate that an endpoint is included, called inclusive.
- An interval that is unbounded at the upper end uses the symbol \(\infty \) as its second term, and an interval that is unbounded at the lower end uses the symbol \(-\infty\) as its first term.
Figure \(\PageIndex{5}\): Summary of interval notation.
![]() Given a line graph, describe the set of values using interval notation
Given a line graph, describe the set of values using interval notation
- Identify the intervals to be included in the set by determining where the graphed line overlays the real number line.
- At the left end of each interval, use "[" for each end value to be included in the set (solid dot) or "(" for each excluded end value (open dot).
- At the right end of each interval, use "]" for each end value to be included in the set (filled dot) or ")" for each excluded end value (open dot).
- Use the union symbol \(\cup\) to combine all intervals into one set.
Another common notation for describing sets when roster notation is not convenient is set-builder notation. For example, \(\{x\;|\;10≤x<30\}\) describes the allowed values of \(x\) in set-builder notation. The braces "\(\{\}\)" are read as “the set of,” and the vertical bar "\(|\)" is read as “such that,” so we would read\( \{x\;|\;10≤x<30\}\) as “the set of \(x\)-values such that 10 is less than or equal to \(x\), and \(x\) is less than 30.”
Set-Builder Notation compared with Interval Notation
Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form\(\{x|\text{ statement about } x\}\) which is read as “the set of all \(x\) such that the statement about \(x\) is true.” For example, we can write
\[\{x\;|\;4<x≤12\}, \nonumber\]
which is the set of all \(x\) such that \(x\) is greater than 4 and less than or equal to 12.
Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example, the same set just given in set-builder notation can also be written in interval notation as
\[\left(4,12\right]. \nonumber\]
Figure \(\PageIndex{6}\) compares graphs, inequality notation, set-builder notation, and interval notation.
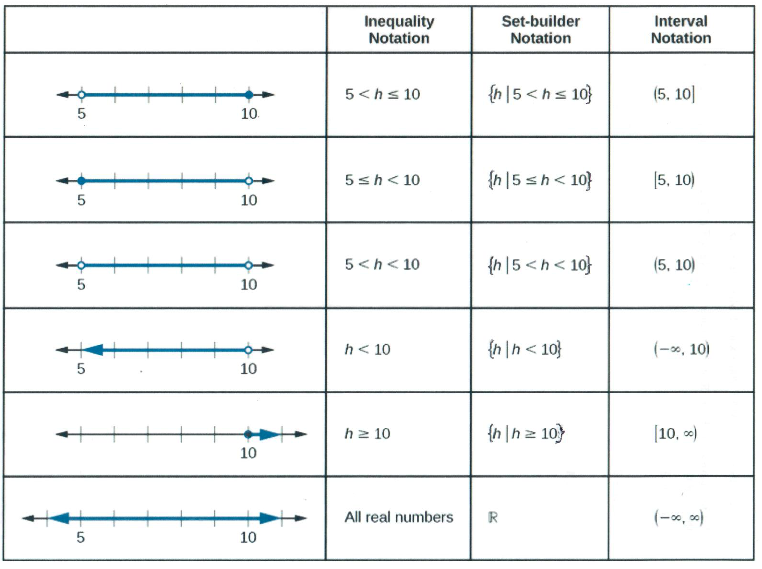
Figure \(\PageIndex{6}\): Summary of notations for inequalities, set-builder, and interval.
If we wish to describe a set of numbers that consists of two or more intervals, we can use \(\cup\) to represent the union of the two sets. An example of a union of two intervals is
\[\{x\;|\; |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right) \nonumber\]
Example \(\PageIndex{4}\): Describing Sets on the Real-Number Line
Describe the intervals of values shown in Figure \(\PageIndex{5}\) using inequality notation, set-builder notation, and interval notation.
![[Line graph of \(1<=x<=3\) and \(5\)]](https://math.libretexts.org/@api/deki/files/867/CNX_Precalc_Figure_01_02_004.jpg?revision=1)
Figure \(\PageIndex{5}\): Line graph of \(1 \leq x \leq 3\) or \(5<x\).
Solution
To describe the values \(x\) included in the intervals shown, we would say, “\(x\) is a real number greater than or equal to 1 and less than or equal to 3, or a real number greater than 5.”
Set-builder Notation\[\{x\;|\;1≤x≤3 \text{ or } x>5\}\nonumber\]
Interval notation
\[[1,3]\cup(5,\infty)\nonumber\]
Remember that when writing or reading interval notation, using a square bracket means the boundary value is included in the set. Using a parenthesis means the boundary value is not included in the set.
![]() \(\PageIndex{6}\)
\(\PageIndex{6}\)
Given Figure \(\PageIndex{6}\), specify the graphed set in
- words
- set-builder notation
- interval notation
![[Line graph of -2<=x, -1<=x<3.]](https://math.libretexts.org/@api/deki/files/877/CNX_Precalc_Figure_01_02_005.jpg?revision=1)
Figure \(\PageIndex{6}\): Line graph of \(x \leq -2\) or \(-1 \leq x<3\).
- Answer
-
a. Values that are less than or equal to –2, or values that are greater than or equal to –1 and less than 3
b. \(\{x\;|\;x≤−2 \text{ or } −1≤x<3\}\)
c. \(\left(−∞,−2\right]\cup\left[−1,3\right)\)

