A: Operations with Integers
- Page ID
- 35107
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)SUMMARY
By the end of this section, you will be able to:
- Add and subtract integers
- Multiply and divide integers
- Simplify expressions with integers
- Evaluate variable expressions with integers
- Translate phrases to expressions with integers
- Use integers in applications
Add and Subtract Integers
Definition: INTEGERS
The whole numbers and their opposites are called the integers.
The integers are the numbers
\[…,-3,-2,-1,0,1,2,3,… \nonumber\]
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more challenging.
We will use two color counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one color (blue) represent positive. The other color (red) will represent the negatives.
We will use two color counters to model addition and subtraction of negatives so that you can visualize the procedures instead of memorizing the rules.
We let one color (blue) represent positive. The other color (red) will represent the negatives.

If we have one positive counter and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero.
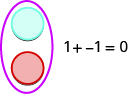
We will use the counters to show how to add:
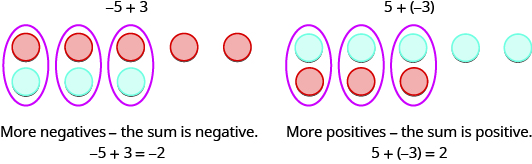
\[5+3 \quad −5+(−3) \quad −5+3 \quad 5+(−3) \nonumber\]
The first example, \(5+3,\) adds 5 positives and 3 positives—both positives.
The second example, \(−5+(−3),\) adds 5 negatives and 3 negatives—both negatives.
When the signs are the same, the counters are all the same color, and so we add them. In each case we get 8—either 8 positives or 8 negatives.

So what happens when the signs are different? Let’s add \[−5+3 \text{ and } 5+(−3). \nonumber\]
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
Example \(\PageIndex{1}\)
Add: a) \(-1+(-4)−1+(-4) \quad \) b) \(-1+5−1+5 \quad\) c) \( 1+(-5)1+(-5).\)
Solution
a)
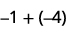 |
|
 |
|
| 1 negative plus 4 negatives is 5 negatives | 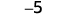 |
b)
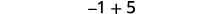 |
|
 |
|
| There are more positives, so the sum is positive. |  |
c)
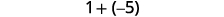 |
|
 |
|
| There are more negatives, so the sum is negative. | 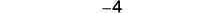 |
Add: ⓐ −2+(−4)−2+(−4) ⓑ −2+4−2+4 ⓒ 2+(−4)2+(−4).
- Answer
-
ⓐ −6−6 ⓑ 22 ⓒ −2−2
EXAMPLE ��ℎ����������10.9Chapter10.9
Add: ⓐ −2+(−5)−2+(−5) ⓑ −2+5−2+5 ⓒ 2+(−5)2+(−5).
- Answer
-
ⓐ −7−7 ⓑ 33 ⓒ −3−3
We will continue to use counters to model the subtraction. Perhaps when you were younger, you read \(“5−3”\) as “5 take away 3.” When you use counters, you can think of subtraction the same way!
We will use the counters to show to subtract:
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \nonumber\]
The first example, \(5−3\), we subtract 3 positives from 5 positives and end up with 2 positives.
In the second example, \(−5−(−3),\) we subtract 3 negatives from 5 negatives and end up with 2 negatives.
Each example used counters of only one color, and the “take away” model of subtraction was easy to apply.
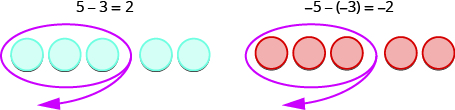
What happens when we have to subtract one positive and one negative number? We’ll need to use both blue and red counters as well as some neutral pairs. If we don’t have the number of counters needed to take away, we add neutral pairs. Adding a neutral pair does not change the value. It is like changing quarters to nickels—the value is the same, but it looks different.
Let’s look at \(-5-3\) and \(5-(-3).\)
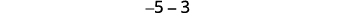 |
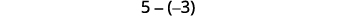 |
|
| Model the first number. |  |
 |
| We now add the needed neutral pairs. |  |
 |
| We remove the number of counters modeled by the second number. | 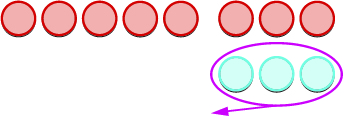 |
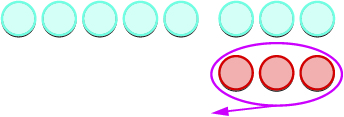 |
| Count what is left. |  |
 |
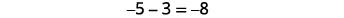 |
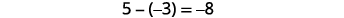 |
|
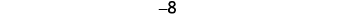 |
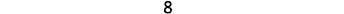 |
EXAMPLE ��ℎ����������10.10Chapter10.10
Subtract: ⓐ 3−13−1 ⓑ −3−(−1)−3−(−1) ⓒ −3−1−3−1 ⓓ 3−(−1)3−(−1).
- Answer
-
ⓐ
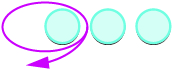
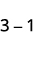
Take 1 positive from 3 positives and get 2 positives. 
ⓑ
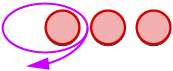
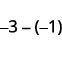
Take 1 positive from 3 negatives and get 2 negatives. 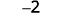
ⓒ

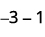
Take 1 positive from the one added neutral pair. 
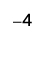
ⓓ

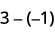
Take 1 negative from the one added neutral pair. 

EXAMPLE ��ℎ����������10.11Chapter10.11
Subtract: ⓐ 6−46−4 ⓑ −6−(−4)−6−(−4) ⓒ −6−4−6−4 ⓓ 6−(−4)6−(−4).
- Answer
-
ⓐ 22 ⓑ −2−2 ⓒ −10−10 ⓓ 1010
Definition: SUBTRACTION PROPERTY
\[a−b=a+(−b) \nonumber\]
Subtracting a number is the same as adding its opposite.
EXAMPLE ��ℎ����������10.13Chapter10.13
Simplify: ⓐ 13−813−8 and 13+(−8)13+(−8) ⓑ −17−9−17−9 and −17+(−9)−17+(−9) ⓒ 9−(−15)9−(−15) and 9+159+15 ⓓ −7−(−4)−7−(−4) and −7+4−7+4.
- Answer
-
ⓐ
Subtract.13−85and13+(−8)513−8and13+(−8)Subtract.55ⓑ
Subtract.−17−9−26and−17+(−9)−26−17−9and−17+(−9)Subtract.−26−26
ⓒ
Subtract.9−(−15)24and9+15249−(−15)and9+15Subtract.2424
ⓓ
Subtract.−7−(−4)−3and−7+4−3−7−(−4)and−7+4Subtract.−3−3
EXAMPLE ��ℎ����������10.14Chapter10.14
Simplify: ⓐ 21−1321−13 and 21+(−13)21+(−13) ⓑ −11−7−11−7 and −11+(−7)−11+(−7) ⓒ 6−(−13)6−(−13) and 6+136+13 ⓓ −5−(−1)−5−(−1) and −5+1−5+1.
- Answer
-
ⓐ 8,88,8 ⓑ −18,−18−18,−18
ⓒ 19,1919,19 ⓓ −4,−4−4,−4
What happens when there are more than three integers? We just use the order of operations as usual.
EXAMPLE ��ℎ����������10.16Chapter10.16
Simplify: 7−(−4−3)−9.7−(−4−3)−9.
- Answer
-
Simplify inside the parentheses first.Subtract left to right.Subtract.7−(−4−3)−97−(−7)−914−957−(−4−3)−9Simplify inside the parentheses first.7−(−7)−9Subtract left to right.14−9Subtract.5
EXAMPLE ��ℎ����������10.17Chapter10.17
Simplify: 8−(−3−1)−9.8−(−3−1)−9.
- Answer
-
3
Multiply and Divide Integers
Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we are using the model just to help us discover the pattern.
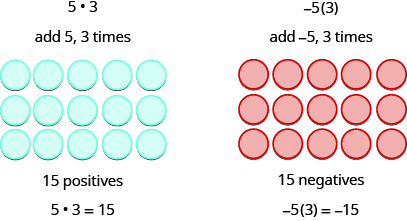
We remember that a⋅b means add a, b times.
The next two examples are more interesting. What does it mean to multiply 5 by −3? It means subtract 5, 3 times. Looking at subtraction as “taking away”, it means to take away 5, 3 times. But there is nothing to take away, so we start by adding neutral pairs on the workspace.
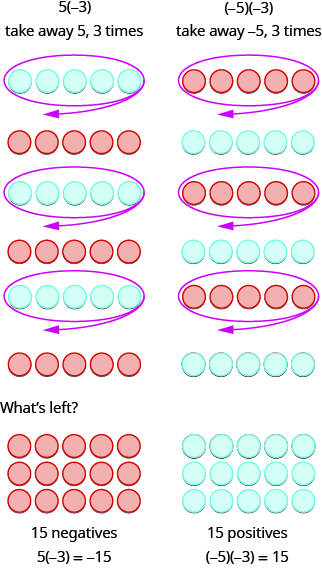
In summary:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Notice that for multiplication of two signed numbers, when the
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
What about division? Division is the inverse operation of multiplication. So, \(15÷3=5\) because \(15·3=15\). In words, this expression says that 15 can be divided into 3 groups of 5 each because adding five three times gives 15. If you look at some examples of multiplying integers, you might figure out the rules for dividing integers.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array} \nonumber\]
Division follows the same rules as multiplication with regard to signs.
MULTIPLICATION AND DIVISION OF SIGNED NUMBERS
For multiplication and division of two signed numbers:
| Same signs | Result |
|---|---|
| • Two positives | Positive |
| • Two negatives | Positive |
If the signs are the same, the result is positive.
| Different signs | Result |
|---|---|
| • Positive and negative | Negative |
| • Negative and positive | Negative |
If the signs are different, the result is negative.
EXAMPLE \(\PageIndex{19}\)
Multiply or divide: ⓐ \(−100÷(−4)\) ⓑ \(7⋅6\) ⓒ \(4(−8)\) ⓓ \(−27÷3.\)
- Answer
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
EXAMPLE \(\PageIndex{20}\)
Multiply or divide: ⓐ \(−115÷(−5)\) ⓑ \(5⋅12\) ⓒ \(9(−7)\) ⓓ\(−63÷7.\)
- Answer
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
When we multiply a number by 1, the result is the same number. Each time we multiply a number by −1, we get its opposite!
MULTIPLICATION BY −1
\[−1a=−a \]
Multiplying a number by \(−1\) gives its opposite.
When an expression has many numbers and many operations in it, remember to multiply and divide in order from left to right.
EXAMPLE \(\PageIndex{25}\)
Simplify: ⓐ \(8(−9)÷(−2)^3\) ⓑ \(−30÷2+(−3)(−7)\).
- Solution
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)

