6.2E: Exercises

Last updated
Save as PDF

Page ID: 18899

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

6.2: Graphs of the Other Trigonometric Functions

This section addresses the graphing of the Tangent, Cosecant, Secant, and Cotangent curves.

Verbal

1) Explain how the graph of the sine function can be used to graph $y=\csc x$.

Answer: Since $y=\csc x$ is the reciprocal function of $y=\sin x$you can plot the reciprocal of the coordinates on the graph of $y=\sin x$ obtain the $y$-coordinates of $y=\csc x$The $x$-intercepts of the graph $y=\sin x$ are the vertical asymptotes for the graph of $y=\csc x$.

2) How can the graph of $y=\cos x$ be used to construct the graph of $y=\sec x$?

3) Explain why the period of $y=\tan x$ is equal to $\pi $.

Answer: Answers will vary. Using the unit circle, one can show that $y=\tan (x+\pi )=\tan x$.

4) Why are there no intercepts on the graph of $y=\csc x$?

5) How does the period of $y=\csc x$ compare with the period of $y=\sin x$?

Answer: The period is the same: $2\pi $

Algebraic

For exercises 6-9, match each trigonometric function with one of the following graphs.

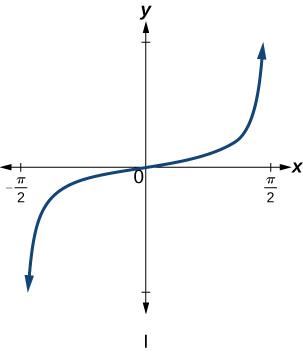
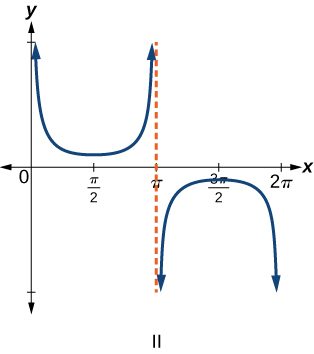
$Ex 6.2.6a.png$ $Ex 6.2.6b.png$

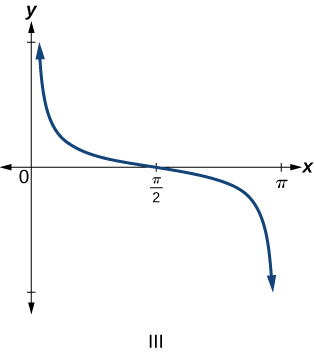
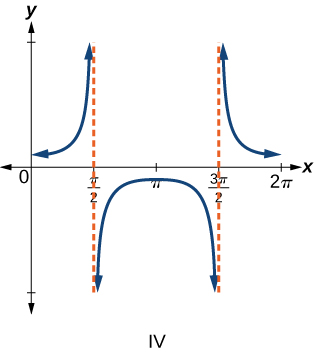
$Ex 6.2.6c.png$ $Ex 6.2.6d.png$

Exercise $\PageIndex{6}$

$f(x)=\tan x$

Answer: $\mathrm{I}$

Exercise $\PageIndex{7}$

$f(x)=\sec x$

Answer: $\mathrm{IV}$

Exercise $\PageIndex{8}$

$f(x)=\csc x$

Answer: $\mathrm{II}$

Exercise $\PageIndex{9}$

$f(x)=\cot x$

Answer: $\mathrm{III}$

For exercises 10-16, find the period and horizontal shift of each of the functions.

10) $f(x)=2\tan(4x-32)$

11) $h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)$

Answer: period: $8$; horizontal shift: $1$ unit to left

12) $m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)$

13) If $\tan x=-1.5$find $\tan (-x)$.

Answer: $1.5$

14) If $\sec x=2$ , find $\sec (-x)$.

15) If $\csc x=-5$ , find $\csc (-x)$.

Answer: $5$

16) If $x\sin x=2$ , find $(-x)\sin (-x)$.

For exercises 17-18, rewrite each expression such that the argument $x$ is positive.

Exercise $\PageIndex{17}$

$\cot(-x)\cos(-x)+\sin(-x)$

Answer: $-\cot x \cos x-\sin x$

18) $\cos(-x)+\tan(-x)\sin(-x)$

Graphical

For the exercises 19-36, sketch two periods of the graph for each of the following functions. Identify the stretching factor, period, and asymptotes.

19) $f(x)=2\tan(4x-32)$

Answer

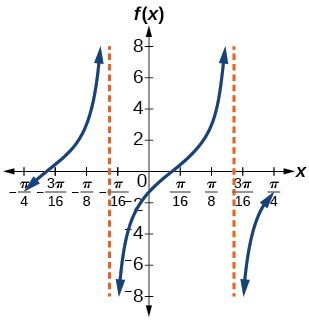
$Ex 6.2.19.png$

stretching factor: $2$; period: $\dfrac{\pi }{3}$asymptotes: $x=\dfrac{1}{4}\left(\dfrac{\pi }{2}+\pi k \right)+8$

20) $h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)$

21) $m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)$

Answer

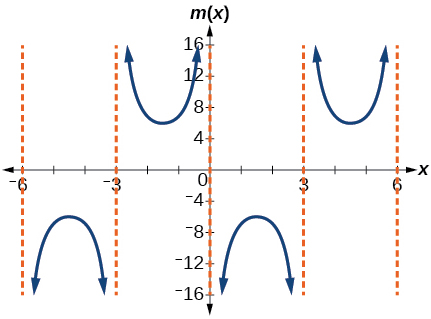
$Ex 6.2.21.png$

stretching factor: $6$; period: $6$; asymptotes: $x=k$

22) $j(x)=\tan \left ( \dfrac{\pi }{2}x \right )$

Exercise $\PageIndex{23}$

$p(x)=\tan \left ( x-\dfrac{\pi }{2} \right )$

Answer

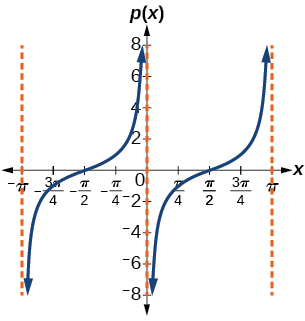
$Ex 6.2.23.png$

stretching factor: $1$; period: $\pi $asymptotes: $x=\pi k$

24) $f(x)=4\tan (x)$

25) $f(x)=\tan \left ( x+\dfrac{\pi }{4} \right )$

Answer

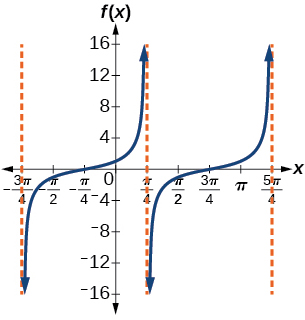
$Ex 6.2.25.png$

Stretching factor: $1$; period: $\pi $asymptotes: $x=\dfrac{\pi}{4}+\pi k$

26) $f(x)=\pi \tan(\pi x- \pi)-\pi$

27) $f(x)=2\csc (x)$

Answer

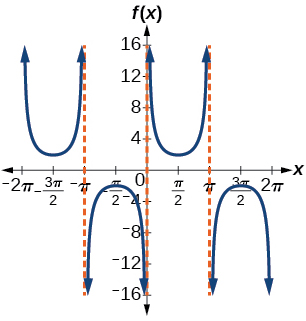
$Ex 6.2.27.png$

stretching factor: $2$; period: $2\pi $asymptotes: $x=\pi k$

28) $f(x)=-\dfrac{1}{4}\csc(x)$

29) $f(x)=4\sec(3x)$

Answer

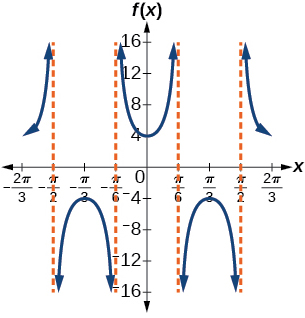
$Ex 6.2.29.png$

stretching factor: $4$; period: $\dfrac{2\pi }{3}$asymptotes: $x=\dfrac{\pi }{6}k$

30) $f(x)=-3\cot(2x)$

31) $f(x)=7\sec(5x)$

Answer

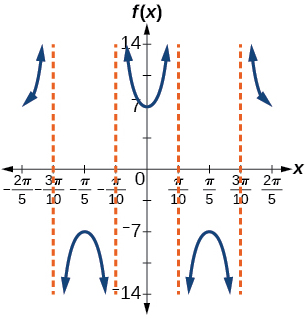
$Ex 6.2.31.png$

stretching factor: $7$; period: $\dfrac{2\pi }{5}$asymptotes: $x=\dfrac{\pi }{10}k$

32) $f(x)=\dfrac{9}{10}\csc(\pi x)$

33) $f(x)=2\csc \left(x+\dfrac{\pi }{4} \right)-1$

Answer

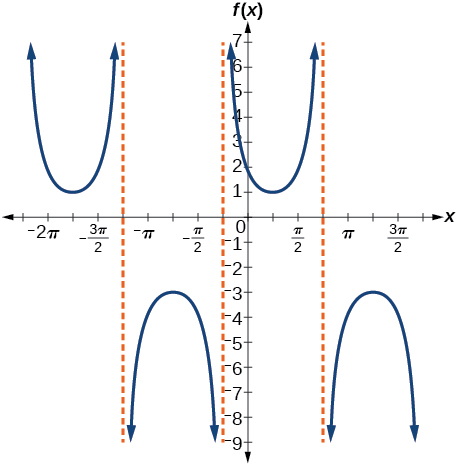
$Ex 6.2.33.png$

Stretching factor: $2$; period: $2\pi $ ; asymptotes: $x=-\dfrac{\pi}{4}+\pi k$ , where $k$ is an integer

34) $f(x)=-\sec \left(x-\dfrac{\pi }{3} \right)-2$

35) $f(x)=\dfrac{7}{5}\csc \left(x-\dfrac{\pi }{4} \right)$

Answer

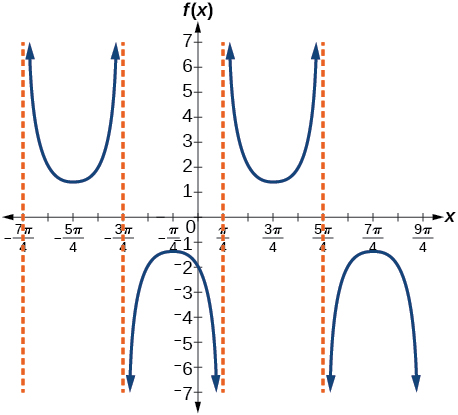
$Ex 6.2.35.png$

Stretching factor: $\dfrac{7}{5}$; period: $2\pi $ ; asymptotes: $x=\dfrac{\pi}{4}+\pi k$ , where $k$ is an integer

36) $f(x)=5\left (\cot \left(x+\dfrac{\pi }{2} \right) -3 \right )$

For the exercises 37-38, find and graph two periods of the periodic function with the given stretching factor, $| A |$, period, and phase shift.

37) A tangent curve, $A=1$period of $\dfrac{\pi }{3}$and phase shift $(h, k)=\left ( \dfrac{\pi }{4},2 \right )$

Answer

$y=\tan\left(3\left(x-\dfrac{\pi}{4} \right) \right)+2$

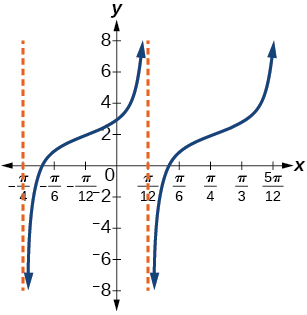
$Ex 6.2.37.png$

38) A tangent curve, $A=-2$ , period of $\dfrac{\pi }{4}$; and phase shift $(h, k)=\left (- \dfrac{\pi }{4},-2 \right )$

For the exercises 39-45, find an equation for the graph of each function.

39)

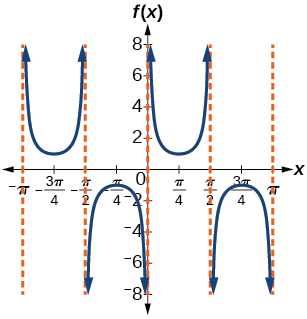
$Ex 6.2.39.png$

Answer: $f(x)=\csc (2x)$

40)

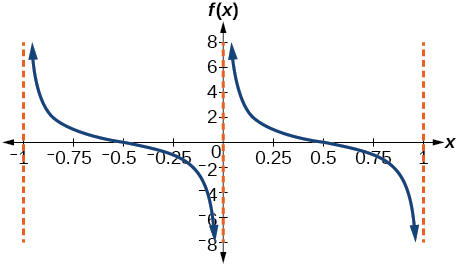
$Ex 6.2.40.png$

41)

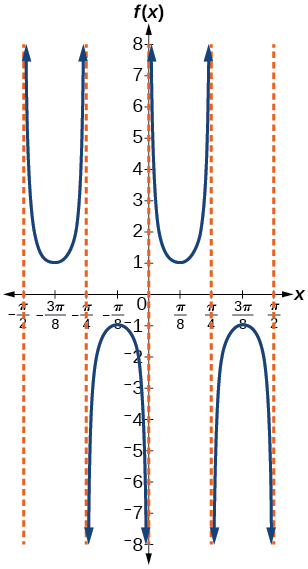
$Ex 6.2.41.png$

Answer: $f(x)=\csc (4x)$

42)

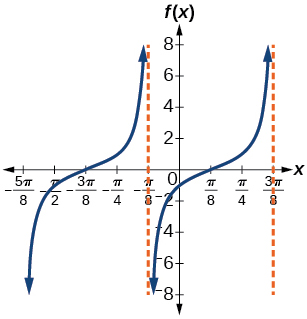
$Ex 6.2.42.png$

43)

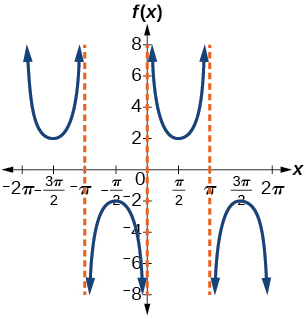
$Ex 6.2.43.png$

Answer: $f(x)=2\csc x$

44)

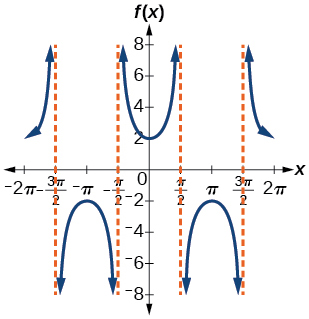
$Ex 6.2.44.png$

45)

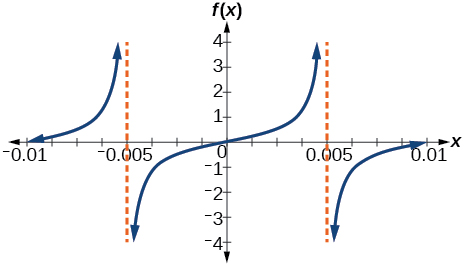
$Ex 6.2.45.png$

Answer: $f(x)=\dfrac{1}{2}\tan (100\pi x)$

Technology

For the exercises 46-53, use a graphing calculator to graph two periods of the given function. Note: most graphing calculators do not have a cosecant button; therefore, you will need to input $\csc x$ as $\dfrac{1}{\sin x}$

46) $f(x)=| \csc (x) |$

47) $f(x)=| \cot (x) |$

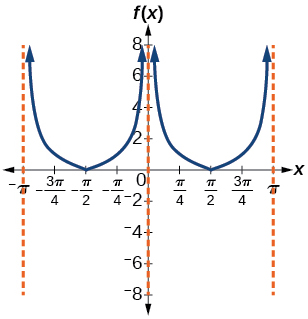
Answer: $Ex 6.2.47.png$

48) $f(x)=2^{\csc (x)}$

49) $f(x)=\frac{\csc (x)}{\sec (x)}$

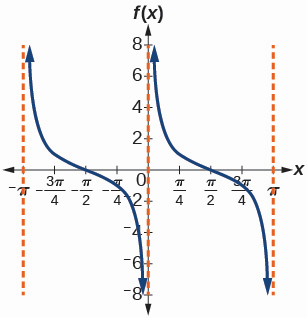
Answer: $Ex 6.2.49.png$

50) Graph $f(x)=1+\sec^2(x)-\tan^2(x)$What is the function shown in the graph?

51) $f(x)=\sec(0.001x)$

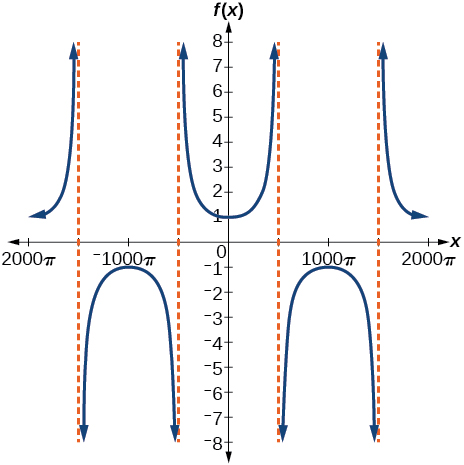
Answer: $Ex 6.2.51.png$

52) $f(x)=\cot(100 \pi x)$

53) $f(x)=\sin^2x +\cos^2x$

Answer: $Ex 6.2.53.png$

Real-World Applications

54) The function $f(x)=20\tan\left(\dfrac{\pi }{10}x\right)$ marks the distance in the movement of a light beam from a police car across a wall for time $x$in seconds, and distance $f(x)$ in feet.

Graph on the interval $[0,5]$
Find and interpret the stretching factor, period, and asymptote.
Evaluate $f(10)$ and $f(2.5)$ and discuss the function’s values at those inputs.

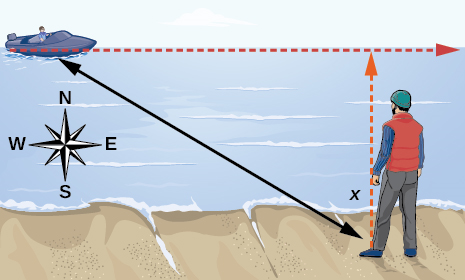
55) Standing on the shore of a lake, a fisherman sights a boat far in the distance to his left. Let $x$ measured in radians, be the angle formed by the line of sight to the ship and a line due north from his position. Assume due north is $0$ and $x$ is measured negative to the left and positive to the right. (See Figure below.) The boat travels from due west to due east and, ignoring the curvature of the Earth, the distance $d(x)$ in kilometers, from the fisherman to the boat is given by the function $d(x)=1.5\sec(x)$

What is a reasonable domain for $d(x)$?
Graph $d(x)$ on this domain.
Find and discuss the meaning of any vertical asymptotes on the graph of $d(x)$.
Calculate and interpret $d\left ( -\dfrac{\pi }{3} \right )$ Round to the second decimal place.
Calculate and interpret $d\left ( \dfrac{\pi }{6} \right )$ Round to the second decimal place.
What is the minimum distance between the fisherman and the boat? When does this occur?

$Ex 6.2.55.png$

Answer

$\left ( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right )$
$Ex 6.2.55b.png$
$x=-\dfrac{\pi }{2}$ and $x=\dfrac{\pi }{2}$the distance grows without bound as $| x |$ approaches $\dfrac{\pi }{2}$—i.e., at right angles to the line representing due north, the boat would be so far away, the fisherman could not see it;
$3$; when $x=-\dfrac{\pi }{3}$the boat is $3$ km away;
$1.73$; when $x=\dfrac{\pi }{6}$the boat is about $1.73$ km away;
$1.5$ km; when $x=0$

56) A laser rangefinder is locked on a comet approaching Earth. The distance $g(x)$in kilometers, of the comet after $x$ days, for $x$ in the interval $0$ to $30$ days, is given by $g(x)=250,000\csc \left(\dfrac{\pi }{30}x \right)$.

Graph $g(x)$ on the interval $[0,35]$.
Evaluate $g(5)$ and interpret the information.
What is the minimum distance between the comet and Earth? When does this occur? To which constant in the equation does this correspond?
Find and discuss the meaning of any vertical asymptotes.

57) A video camera is focused on a rocket on a launching pad $2$ miles from the camera. The angle of elevation from the ground to the rocket after $x$ seconds is $\dfrac{\pi }{120}x$.

Write a function expressing the altitude $h(x)$in miles, of the rocket above the ground after $x$ seconds. Ignore the curvature of the Earth.
Graph $h(x)$ on the interval $(0,60)$.
Evaluate and interpret the values $h(0)$ and $h(30)$.
What happens to the values of $h(x)$ as $x$ approaches $60$ seconds? Interpret the meaning of this in terms of the problem.

Answer

$h(x)=2\tan \left(\dfrac{\pi }{120}x \right)$
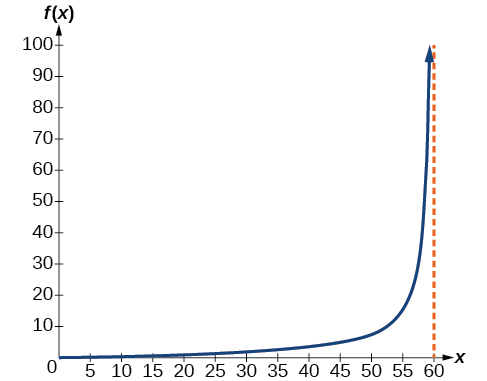
$Ex 6.2.57b.png$
$h(0)=0$after $0$ seconds, the rocket is $0$ mi above the ground; $h(30)=2$after $30$ seconds, the rockets is $2$ mi high;
As $x$ approaches $60$ seconds, the values of $h(x)$ grow increasingly large. The distance to the rocket is growing so large that the camera can no longer track it.