1.2E: Exercises

1.2E: Exercises

Verbal

Exercise 1.2.1

Why does the domain differ for different functions?

Answer:

The domain of a function depends upon what values of the independent variable make the function undefined or imaginary.

Exercise 1.2.2

How do we determine the domain of a function defined by an equation?

Exercise 1.2.3

Explain why the domain of 𝑓⁡(𝑥) =3√𝑥 is different from the domain of 𝑓⁡(𝑥) =√𝑥.

Answer:

There is no restriction on x for 𝑓⁡(𝑥) =3√𝑥 because you can take the cube root of any real number. So the domain is all real numbers, (−∞,∞). When dealing with the set of real numbers, you cannot take the square root of negative numbers. So x-values are restricted for 𝑓⁡(𝑥) =√𝑥 to nonnegative numbers and the domain is [0,∞).

Exercise 1.2.4

When describing sets of numbers using interval notation, when do you use a parenthesis and when do you use a bracket?

Exercise 1.2.5

How do you graph a piecewise function?

Answer:

Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x-axis and y-axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate −∞ or ∞. Combine the graphs to find the graph of the piecewise function.

Algebraic

For the following exercises, find the domain of each function using interval notation.

Exercise 1.2.6

𝑓⁡(𝑥) =−2⁢𝑥⁢(𝑥 −1)⁢(𝑥 −2)

Exercise 1.2.7

𝑓⁡(𝑥) =5 −2⁢𝑥2

Answer:

(−∞,∞)

Exercise 1.2.8

𝑓⁡(𝑥) =3⁢√𝑥−2

Exercise 1.2.9

𝑓⁡(𝑥) =3 −√6−2⁢𝑥

Answer:

(−∞,3]

Exercise 1.2.10

𝑓⁡(𝑥) =√4−3⁢𝑥

Exercise 1.2.11

𝑓⁡(𝑥) =√𝑥2+4

Answer:

(−∞,∞)

Exercise 1.2.12

𝑓⁡(𝑥) =3√1−2⁢𝑥(f

Exercise 1.2.13

𝑓⁡(𝑥) =3√𝑥−1(f

Answer:

(−∞,∞)

Exercise 1.2.14

𝑓⁡(𝑥) =9𝑥−6

Exercise 1.2.15

𝑓⁡(𝑥) =3⁢𝑥+14⁢𝑥+2

Answer:

(−∞,−12) ∪(−12,∞)

Exercise 1.2.16

𝑓⁡(𝑥) =√𝑥+4𝑥−4

Exercise 1.2.17

𝑓⁡(𝑥) =𝑥−3𝑥2+9⁢𝑥−22

Answer:

(−∞,−11) ∪(−11,2) ∪(2,∞)

Exercise 1.2.18

𝑓⁡(𝑥) =1𝑥2−𝑥−6

Exercise 1.2.19

𝑓⁡(𝑥) =2⁢𝑥3−250𝑥2−2⁢𝑥−15

Answer:

(−∞,−3) ∪(−3,5) ∪(5,∞)

Exercise 1.2.20

5√𝑥−3

Exercise 1.2.21

2⁢𝑥+1√5−𝑥

Answer:

(−∞,5)

Exercise 1.2.22

√𝑥−4√𝑥−6

Exercise 1.2.23

√𝑥−6√𝑥−4

Answer:

[6,∞)

Exercise 1.2.24

𝑓⁡(𝑥) =𝑥𝑥

Exercise 1.2.25

𝑓⁡(𝑥) =𝑥2−9⁢𝑥𝑥2−81

Answer:

(−∞,−9) ∪(−9,9) ∪(9,∞)

Exercise 1.2.26

Find the domain of the function 𝑓⁡(𝑥) =√2⁢𝑥3−50⁢𝑥 by:

a. using algebra

b. graphing the function in the radicand and determining intervals on the x-axis for which the radicand is nonnegative..

Graphical

For the following exercises, write the domain and range of each function using interval notation.

Exercise 1.2.27

Answer:

domain: (2,8], range [6,8)

Exercise 1.2.28

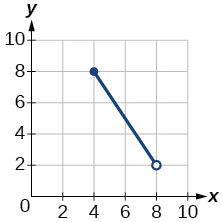
Exercise 1.2.29

Answer:

domain: [−4,4], range: [0,2]

Exercise 1.2.30

Exercise 1.2.31

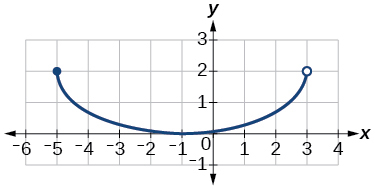
Answer:

domain: [−5,3), range: [0,2]

Exercise 1.2.32

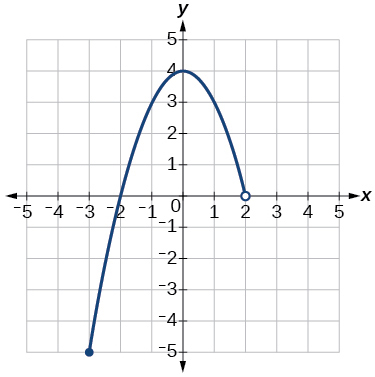
Exercise 1.2.33

Answer:

domain: (−∞,1], range: [0,∞)

Exercise 1.2.34

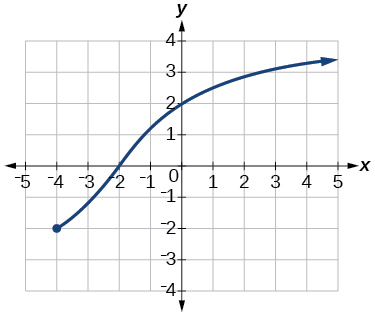
Exercise 1.2.35

Answer:

domain: [−6,−16] ∪[16,6]; range: [−6,−16] ∪[16,6]

Exercise 1.2.36

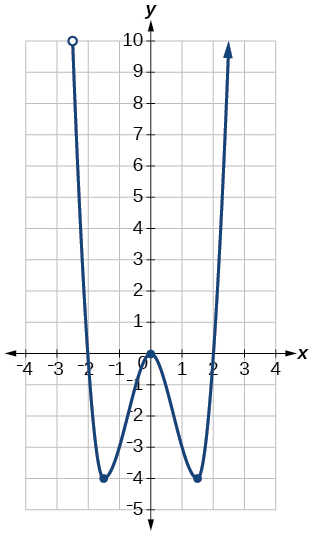
Exercise 1.2.37

Answer:

domain: [−3,∞); range: [0,∞)

For the following exercises, sketch a graph of the piecewise function. Write the domain in interval notation.

Exercise 1.2.38

𝑓⁡(𝑥) ={𝑥+1if 𝑥<−2−2⁢𝑥−3if 𝑥≥−2

Exercise 1.2.39

𝑓⁡(𝑥) ={2⁢𝑥−1if 𝑥<11+𝑥if 𝑥≥1

Answer:

domain: (−∞,∞)

Exercise 1.2.40

𝑓⁡(𝑥) ={𝑥+1if 𝑥<0𝑥−1if 𝑥>0

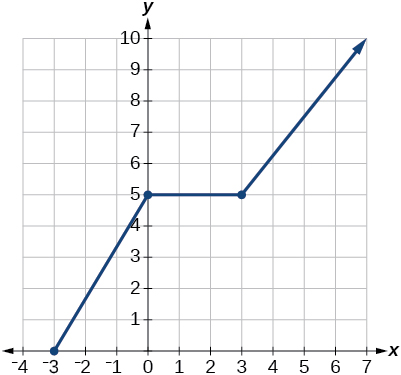
Exercise 1.2.41

𝑓⁡(𝑥) ={3if 𝑥<0√𝑥if 𝑥≥0

Answer:

domain: (−∞,∞)

Exercise 1.2.42

𝑓⁡(𝑥) ={𝑥2if 𝑥<01−𝑥if 𝑥>0

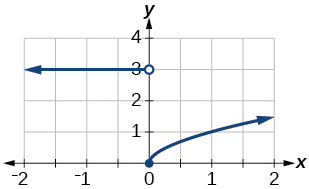
Exercise 1.2.43

𝑓⁡(𝑥) ={𝑥2if 𝑥<0𝑥+2if 𝑥≥0

Answer:

domain: (−∞,∞)

Exercise 1.2.44

𝑓⁡(𝑥) ={𝑥+1if 𝑥<1𝑥3if 𝑥≥1

Exercise 1.2.45

𝑓⁡(𝑥) ={|𝑥|if 𝑥<21if 𝑥≥2

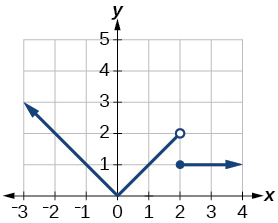
Answer:

domain: (−∞,∞)

Numeric

For the following exercises, given each function 𝑓, evaluate 𝑓⁡(−3), 𝑓⁡(−2), 𝑓⁡(−1), and 𝑓⁡(0).

Exercise 1.2.46

𝑓⁡(𝑥) ={𝑥+1if 𝑥<−2−2⁢𝑥−3if 𝑥≥−2

Exercise 1.2.47

𝑓⁡(𝑥) ={1if 𝑥≤−30if 𝑥>−3

Answer:

𝑓⁡(−3) =1; 𝑓⁡(−2) =0; 𝑓⁡(−1) =0; 𝑓⁡(0) =0

Exercise 1.2.48

𝑓⁡(𝑥) ={−2⁢𝑥2+3if 𝑥≤−15⁢𝑥−7if 𝑥>−1

For the following exercises, given each function 𝑓, evaluate 𝑓⁡(−1), 𝑓⁡(0), 𝑓⁡(2), and 𝑓⁡(4).

Exercise 1.2.49

𝑓⁡(𝑥) ={7⁢𝑥+3if 𝑥<07⁢𝑥+6if 𝑥≥0

Answer:

𝑓⁡(−1) =−4; 𝑓⁡(0) =6; 𝑓⁡(2) =20; 𝑓⁡(4) =34

Exercise 1.2.50

𝑓⁡(𝑥) ={𝑥2−2if 𝑥<24+|𝑥−5|if 𝑥≥2

Exercise 1.2.51

𝑓⁡(𝑥) =⎧{ {⎨{ {⎩5⁢𝑥if 𝑥<03if 0≥𝑥≤2𝑥2if 𝑥>3

Answer:

𝑓⁡(−1) =−5; 𝑓⁡(0) =3; 𝑓⁡(2) =3; 𝑓⁡(4) =16

For the following exercises, write the domain for the piecewise function in interval notation.

Exercise 1.2.52

𝑓⁡(𝑥) ={𝑥+1if 𝑥<−2−2⁢𝑥−3if 𝑥≥−2

Exercise 1.2.53

𝑓⁡(𝑥) ={𝑥2−2if 𝑥<1−𝑥2+2if 𝑥>1

Answer:

domain: (−∞,1) ∪(1,∞)

Exercise 1.2.54

𝑓⁡(𝑥) ={𝑥2−3if 𝑥<0−3⁢𝑥2if 𝑥≥2

Technology

Exercise 1.2.55

Graph 𝑦 =1𝑥2 on the viewing window [−0.5,−0.1] and [0.1,0.5]. Determine the corresponding range for the viewing window. Show the graphs.

Answer:

window: [−0.5,−0.1]; range: [4,100]

window: [0.1,0.5]; range: [4,100]

Exercise 1.2.56

Graph 𝑦 =1𝑥 on the viewing window [−0.5,−0.1] and [0.1,0.5]. Determine the corresponding range for the viewing window. Show the graphs.

Extension

Exercise 1.2.57

Suppose the range of a function 𝑓 is [−5,8]. What is the range of |𝑓⁡(𝑥)|?

Answer:

[0,8]

Exercise 1.2.58

Create a function in which the range is all nonnegative real numbers.

Exercise 1.2.59

Create a function in which the domain is 𝑥 >2.

Answer:

Many answers. One function is 𝑓⁡(𝑥) =1√𝑥−2.

Real-World Applications

Exercise 1.2.60

The height ℎ of a projectile is a function of the time 𝑡 it is in the air. The height in feet for 𝑡 seconds is given by the function ℎ⁡(𝑡) =−16⁢𝑡2 +96⁢𝑡. What is the domain of the function? What does the domain mean in the context of the problem?

Answer:

The domain is [0,6]; it takes 6 seconds for the projectile to leave the ground and return to the ground.

Exercise 1.2.61

The cost in dollars of making 𝑥 items is given by the function 𝐶⁡(𝑥) =10⁢𝑥 +500.

a. The fixed cost is determined when zero items are produced. Find the fixed cost for this item.

b. What is the cost of making 25 items?

c. Suppose the maximum cost allowed is $1500. What are the domain and range of the cost function, 𝐶⁡(𝑥)?