1.3E: Exercises
This page is a draft and is under active development.
( \newcommand{\kernel}{\mathrm{null}\,}\)
Verbal
Verbal
Exercise 1.3.1
Can the average rate of change of a function be constant?
- Answer:
- Yes, the average rate of change of all linear functions is constant.
Exercise 1.3.2
If a function f is increasing on (a,b) and decreasing on (b,c), then what can be said about the local extremum of f on (a,c)?
Exercise 1.3.3
How are the absolute maximum and minimum similar to and different from the local extrema?
- Answer:
- The absolute maximum and minimum relate to the entire graph, whereas the local extrema relate only to a specific region around an open interval.
Exercise 1.3.4
How does the graph of the absolute value function compare to the graph of the quadratic function, y=x2, in terms of increasing and decreasing intervals?
Algebraic
For the following exercises, find the average rate of change of each function on the interval specified for real numbers b or h.
Exercise 1.3.5
f(x)=4x2−7 on [1,b]
- Answer:
- 4(b+1)
Exercise 1.3.6
g(x)=2x2−9 on [4,b]
Exercise 1.3.7
p(x)=3x+4 on [2,2+h]
- Answer:
- 3
Exercise 1.3.8
k(x)=4x−2 on [3,3+h]
Exercise 1.3.9
f(x)=2x2+1 on [x,x+h]
- Answer:
- 4x+2h
Exercise 1.3.10
g(x)=3x2−2 on [x,x+h]
Exercise 1.3.11
a(t)=1t+4 on [9,9+h]
- Answer:
- −113(13+h)
Exercise 1.3.12
b(x)=1x+3 on [1,1+h]
Exercise 1.3.13
j(x)=3x3 on [1,1+h]
- Answer:
- 3h2+9h+9
Exercise 1.3.14
r(t)=4t3 on [2,2+h]
Exercise 1.3.15
f(x+h)−f(x)h given f(x)=2x2−3x on [x,x+h]
- Answer:
- 4x+2h−3
Graphical
For the following exercises, consider the graph of f shown in Figure 1.3.15.
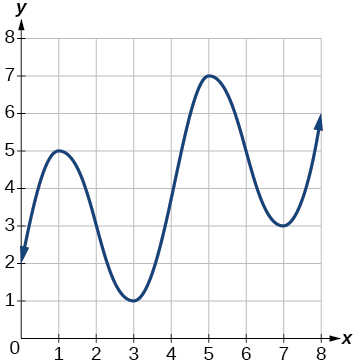
Figure 1.3.15: Graph of a polynomial.
Exercise 1.3.16
Estimate the average rate of change from x=1 to x=4.
Exercise 1.3.17
Estimate the average rate of change from x=2 to x=5.
- Answer:
- 43
Exercise 1.3.18

Exercise 1.3.19
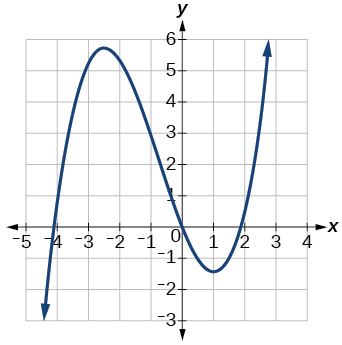
- Answer:
- increasing on (−∞,−2.5)∪(1,∞), decreasing on (−2.5,1)
Exercise 1.3.20
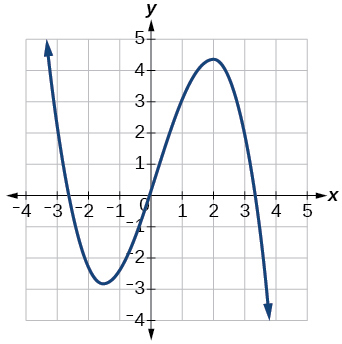
Exercise 1.3.21
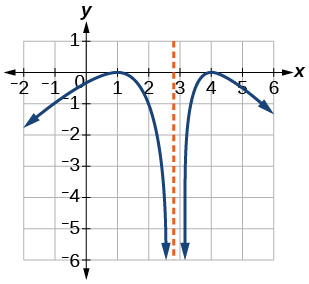
- Answer:
- increasing on (−∞,1)∪(3,4), decreasing on (1,3)∪(4,∞)
For the following exercises, consider the graph shown in Figure 16.
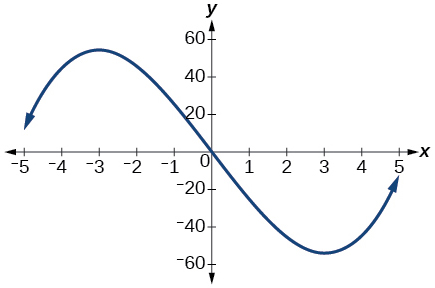
Figure 16: Graph of a cubic function.
Exercise 1.3.22
Estimate the intervals where the function is increasing or decreasing.
Exercise 1.3.23
Estimate the point(s) at which the graph of f has a local maximum or a local minimum.
- Answer:
- local maximum: (−3,60), local minimum: (3,−60)
For the following exercises, consider the graph in Figure 17.
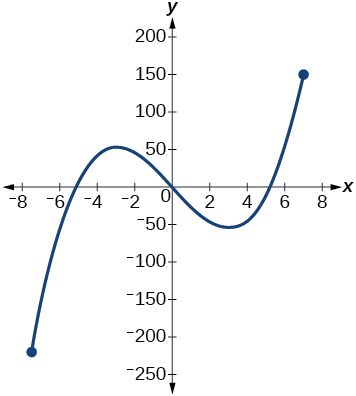
Figure 17: Graph of a cubic function.
Exercise 1.3.24
If the complete graph of the function is shown, estimate the intervals where the function is increasing or decreasing.
Exercise 1.3.25
If the complete graph of the function is shown, estimate the absolute maximum and absolute minimum.
- Answer:
- absolute maximum at approximately (7,150), absolute minimum at approximately (−7.5,−220)
Numeric
Exercise 1.3.26
The table below gives the annual sales (in millions of dollars) of a product from 1998 to 2006. What was the average rate of change of annual sales (a) between 2001 and 2002, and (b) between 2001 and 2004?
| Year | Sales (millions of dollars) |
| 1998 | 201 |
| 1999 | 219 |
| 2000 | 233 |
| 2001 | 243 |
| 2002 | 249 |
| 2003 | 251 |
| 2004 | 249 |
| 2005 | 243 |
| 2006 | 233 |
Exercise 1.3.27
The table below gives the population of a town (in thousands) from 2000 to 2008. What was the average rate of change of population (a) between 2002 and 2004, and (b) between 2002 and 2006?
| Year | Population (thousands) |
| 2000 | 87 |
| 2001 | 84 |
| 2002 | 83 |
| 2003 | 80 |
| 2004 | 77 |
| 2005 | 76 |
| 2006 | 78 |
| 2007 | 81 |
| 2008 | 85 |
- Answer:
- a. –3000
b. –1250
For the following exercises, find the average rate of change of each function on the interval specified.
Exercise 1.3.28
f(x)=x2 on [1,5]
Exercise 1.3.29
h(x)=5−2x2 on [−2,4]
- Answer:
- -4
Exercise 1.3.30
q(x)=x3 on [−4,2]
Exercise 1.3.31
g(x)=3x3−1 on [−3,3]
- Answer:
- 27
Exercise 1.3.32
y=1x on [1,3]
Exercise 1.3.33
p(t)=(t2−4)(t+1)t2+3 on [−3,1]
- Answer:
- –0.167
Exercise 1.3.34
k(t)=6t2+4t3 on [−1,3]
Technology
For the following exercises, use a graphing utility to estimate the local extrema of each function and to estimate the intervals on which the function is increasing and decreasing.
Exercise 1.3.35
f(x)=x4−4x3+5
- Answer:
- Local minimum at (3,−22), decreasing on (−∞,3), increasing on (3,∞)
Exercise 1.3.36
h(x)=x5+5x4+10x3+10x2−1
Exercise 1.3.37
g(t)=t√t+3
- Answer:
- Local minimum at (−2,−2), decreasing on (−3,−2), increasing on (−2,∞)
Exercise 1.3.38
k(t)=3t23−t
Exercise 1.3.39
m(x)=x4+2x3−12x2−10x+4
- Answer:
- Local maximum at (−0.5,6), local minima at (−3.25,−47) and (2.1,−32), decreasing on (−∞,−3.25) and (−0.5,2.1), increasing on (−3.25,−0.5) and (2.1,∞)
Exercise 1.3.40
n(x)=x4−8x3+18x2−6x+2
Extension
Exercise 1.3.41
The graph of the function f is shown in Figure 18
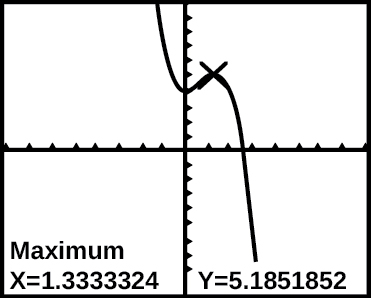
Figure 18: Graph of f(x) on a graphing calculator.
Based on the calculator screen shot, the point (1.333,5.185) is which of the following?
A. a relative (local) maximum of the function
B. the vertex of the function
C. the absolute maximum of the function
D. a zero of the function
- Answer:
- A
Exercise 1.3.42
Let f(x)=1x. Find a number c such that the average rate of change of the function f on the interval (1,c) is −14.
Exercise1.3.43
Let f(x)=1x. Find the number b such that the average rate of change of f on the interval (2,b) is −110.
- Answer:
- b=5
Real-World Applications
Exercise 1.3.44
At the start of a trip, the odometer on a car read 21,395. At the end of the trip, 13.5 hours later, the odometer read 22,125. Assume the scale on the odometer is in miles. What is the average speed the car traveled during this trip?
Exercise 1.3.45
A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the time read exactly 3:40 p.m. At this time, he started pumping gas into the tank. At exactly 3:44, the tank was full and he noticed that he had pumped 10.7 gallons. What is the average rate of flow of the gasoline into the gas tank?
- Answer:
- 2.7 gallons per minute
Exercise 1.3.46
Near the surface of the moon, the distance that an object falls is a function of time. It is given by d(t)=2.6667t2, where t is in seconds and d(t) is in feet. If an object is dropped from a certain height, find the average velocity of the object from t=1 to t=2.
Exercise 1.3.47
The graph in Figure 19 illustrates the decay of a radioactive substance over t days.
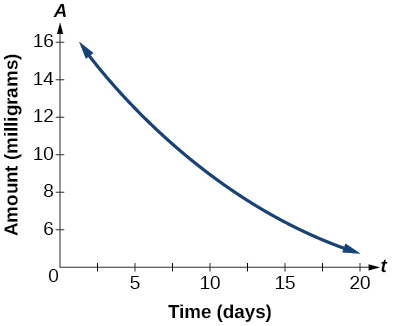
Figure 19: Graph of an exponential function.
Use the graph to estimate the average decay rate from t=5 to t=15.
- Answer:
- approximately –0.6 milligrams per day

