1.4E: Exercises

1.4: Composition of Functions

Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. The cost depends on the temperature, and the temperature depends on the day. By combining these two relationships into one function, we have performed function composition, which is the focus of this section.

Section Exercises

Verbal

Exercise 1.4.1

How does one find the domain of the quotient of two functions, 𝑓𝑔?

Answer:

Find the numbers that make the function in the denominator 𝑔 equal to zero, and check for any other domain restrictions on 𝑓 and 𝑔, such as an even-indexed root or zeros in the denominator.

Exercise 1.4.2

What is the composition of two functions, 𝑓 ∘𝑔?

Exercise 1.4.3

If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition? If yes, give an example. If no, explain why not.

Answer:

Yes. Sample answer: Let 𝑓⁡(𝑥) =𝑥 +1 and 𝑔⁡(𝑥) =𝑥 −3. Then 𝑓⁡(𝑔⁡(𝑥)) =𝑓⁡(𝑥 −3) =(𝑥 −3) +1 =𝑥 −2 and 𝑔⁡(𝑓⁡(𝑥)) =𝑔⁡(𝑥 +1) =(𝑥 +1) −3 =𝑥 −2. So 𝑓 ∘𝑔 =𝑔 ∘𝑓.

Exercise 1.4.4

How do you find the domain for the composition of two functions, 𝑓 ∘𝑔?

Algebraic

Exercise 1.4.5

Given 𝑓⁡(𝑥) =𝑥2 +2⁢𝑥 and 𝑔⁡(𝑥) =6 −𝑥2, find 𝑓 +𝑔, 𝑓 −𝑔, 𝑓⁡𝑔, and 𝑓𝑔.Determine the domain for each function in interval notation.

Answer:

(𝑓 +𝑔)⁡(𝑥) =2⁢𝑥 +6, domain: (−∞,∞)

(𝑓 −𝑔)⁡(𝑥) =2⁢𝑥2 +2⁢𝑥 −6, domain: (−∞,∞)

(𝑓⁡𝑔)⁢(𝑥) =−𝑥4 −2⁢𝑥3 +6⁢𝑥2 +12⁢𝑥, domain: (−∞,∞)

(𝑓𝑔)⁡(𝑥) =𝑥2+2⁢𝑥6−𝑥2, domain: (−∞,−√6) ∪(√6,√6) ∪(√6,∞)

Exercise 1.4.6

Given 𝑓⁡(𝑥) =−3⁢𝑥2 +𝑥 and 𝑔⁡(𝑥) =5, find 𝑓 +𝑔, 𝑓 −𝑔, 𝑓⁡𝑔, and 𝑓𝑔. Determine the domain for each function in interval notation.

Exercise 1.4.7

Given 𝑓⁡(𝑥) =2⁢𝑥2 +4⁢𝑥 and 𝑔⁡(𝑥) =12⁢𝑥, find 𝑓 +𝑔, 𝑓 −𝑔, 𝑓⁡𝑔, and 𝑓𝑔. Determine the domain for each function in interval notation.

Answer:

(𝑓 +𝑔)⁡(𝑥) =4⁢𝑥3+8⁢𝑥2+12⁢𝑥, domain: (−∞,0) ∪(0,∞)

(𝑓 −𝑔)⁡(𝑥) =4⁢𝑥⁢3+8⁢𝑥⁢2−12⁢𝑥, domain: (−∞,0) ∪(0,∞)

(𝑓⁡𝑔)⁢(𝑥) =𝑥 +2, domain: (−∞,0) ∪(0,∞)

(𝑓⁡𝑔)⁢(𝑥) =4⁢𝑥3 +8⁢𝑥2, domain: (−∞,0) ∪(0,∞)

Exercise 1.4.8

Given 𝑓⁡(𝑥) =1𝑥−4 and 𝑔⁡(𝑥) =16−𝑥, find𝑓 +𝑔, 𝑓 −𝑔, 𝑓⁡𝑔, and 𝑓𝑔. Determine the domain for each function in interval notation.

Exercise 1.4.9

Given 𝑓⁡(𝑥) =3⁢𝑥2 and 𝑔⁡(𝑥) =√𝑥−5, find 𝑓 +𝑔, 𝑓 −𝑔, 𝑓⁡𝑔, and 𝑓𝑔. Determine the domain for each function in interval notation.

Answer:

(𝑓 +𝑔)⁡(𝑥) =3⁢𝑥2 +√𝑥−5, domain: [5,∞)

(𝑓 −𝑔)⁡(𝑥) =3⁢𝑥2 −√𝑥−5, domain: [5,∞)

(𝑓⁡𝑔)⁢(𝑥) =3⁢𝑥2⁢√𝑥−5, domain: [5,∞)

(𝑓𝑔)⁡(𝑥) =3⁢𝑥2√𝑥−5, domain: (5,∞)

Exercise 1.4.10

Given 𝑓⁡(𝑥) =√𝑥 and 𝑔⁡(𝑥) =|𝑥 −3|, find 𝑔𝑓. Determine the domain of the function in interval notation.

Exercise 1.4.11

Given 𝑓⁡(𝑥) =2⁢𝑥2 +1 and 𝑔⁡(𝑥) =3⁢𝑥 −5, find the following:

a. 𝑓⁡(𝑔⁡(2))
b. 𝑓⁡(𝑔⁡(𝑥))
c. 𝑔⁡(𝑓⁡(𝑥))
d. (𝑔 ∘𝑔)⁡(𝑥)
e. (𝑓 ∘𝑓)⁡(−2)

Answer:

a. 3;
b. 𝑓⁡(𝑔⁡(𝑥)) =2⁢(3⁢𝑥−5)2 +1
c. 𝑓⁡(𝑔⁡(𝑥)) =6⁢𝑥2 −2
d. (𝑓 ∘𝑔)⁡(𝑥) =3⁢(3⁢𝑥 −5) −5 =9⁢𝑥 −20
e. (𝑓 ∘𝑓)⁡(−2) =163

For the following exercises, use each pair of functions to find 𝑓⁡(𝑔⁡(𝑥)) and 𝑔⁡(𝑓⁡(𝑥)). Simplify your answers.

Exercise 1.4.12

𝑓⁡(𝑥) =𝑥2 +1, 𝑔⁡(𝑥) =√𝑥+2

Exercise 1.4.13

𝑓⁡(𝑥) =√𝑥 +2, 𝑔⁡(𝑥) =𝑥2 +3

Answer:

𝑓⁡(𝑔⁡(𝑥)) =√𝑥+3, 𝑔⁡(𝑓⁡(𝑥)) =𝑥 +4⁢√𝑥 +7

Exercise 1.4.14

𝑓⁡(𝑥) =|𝑥|, 𝑔⁡(𝑥) =5⁢𝑥 +1

Exercise 1.4.15

𝑓⁡(𝑥) =3√𝑥, 𝑔⁡(𝑥) =𝑥+1𝑥3

Answer:

𝑓⁡(𝑔⁡(𝑥)) =3√𝑥+1𝑥3 =3√𝑥+1𝑥, 𝑔⁡(𝑓⁡(𝑥)) =3√𝑥+1𝑥



Exercise 1.4.16

𝑓⁡(𝑥) =1𝑥−6, 𝑔⁡(𝑥) =7𝑥 +6

Exercise 1.4.17

𝑓⁡(𝑥) =1𝑥−4, 𝑔⁡(𝑥) =2𝑥 +4

Answer:

(𝑓 ∘𝑔)⁡(𝑥) =12𝑥+4−4 =𝑥2, (𝑔 ∘𝑓)⁡(𝑥) =2⁢𝑥 −4

For the following exercises, use each set of functions to find f(g(h(x))). Simplify your answers.

Exercise 1.4.18

𝑓⁡(𝑥) =𝑥4 +6, 𝑔⁡(𝑥) =𝑥 −6, and ℎ⁡(𝑥) =√𝑥

Exercise 1.4.19

𝑓⁡(𝑥) =𝑥2 +1, 𝑔⁡(𝑥) =1𝑥, and ℎ⁡(𝑥) =𝑥 +3

Answer:

𝑓⁡(𝑔⁡(ℎ⁡(𝑥))) =(1𝑥+3)2 +1

Exercise 1.4.20

Given 𝑓⁡(𝑥) =1𝑥 and 𝑔⁡(𝑥) =𝑥 −3, find the following:

a. (𝑓 ∘𝑔)⁡(𝑥)
b. the domain of (𝑓 ∘𝑔)⁡(𝑥) in interval notation
c. (𝑔 ∘𝑓)⁡(𝑥)
d. the domain of (𝑔 ∘𝑓)⁡(𝑥)
3. (𝑓𝑔)⁡𝑥

Exercise 1.4.21

Given 𝑓⁡(𝑥) =√2−4⁢𝑥 and 𝑔⁡(𝑥) =−3𝑥, find the following:

a. (𝑔 ∘𝑓)⁡(𝑥)
b. the domain of (𝑔 ∘𝑓)⁡(𝑥) in interval notation

Answer:

a. (𝑔 ∘𝑓)⁡(𝑥) =−3√2−4⁢𝑥
b. (−∞,12)

Exercise 1.4.22

Given the functions 𝑓⁡(𝑥) =1−𝑥𝑥 and 𝑔⁡(𝑥) =11+𝑥2, find the following:

a. (𝑔 ∘𝑓)⁡(𝑥)
b. (𝑔 ∘𝑓)⁡(2)

Exercise 1.4.23

Given functions 𝑝⁡(𝑥) =1√𝑥 and 𝑚⁡(𝑥) =𝑥2 −4, state the domain of each of the following functions using interval notation:

a. 𝑝⁡(𝑥)𝑚⁡(𝑥)
b. 𝑝⁡(𝑚⁡(𝑥))
c. 𝑚⁡(𝑝⁡(𝑥))

Answer:

a. (0,2) ∪(2,∞)
b. (−∞,−2) ∪(2,∞)
c. (0,∞)

Exercise 1.4.24

Given functions 𝑞⁡(𝑥) =1√𝑥 and ℎ⁡(𝑥) =𝑥2 −9, state the domain of each of the following functions using interval notation.

a. 𝑞⁡(𝑥)ℎ⁡(𝑥)
b. 𝑞⁡(ℎ⁡(𝑥))
c. ℎ⁡(𝑞⁡(𝑥))

Exercise 1.4.25

For 𝑓⁡(𝑥) =1𝑥 and 𝑔⁡(𝑥) =√𝑥−1, write the domain of (𝑓 ∘𝑔)⁡(𝑥) in interval notation.

Answer:

(1,∞)

For the following exercises, find functions 𝑓⁡(𝑥) and 𝑔⁡(𝑥) so the given function can be expressed as ℎ⁡(𝑥) =𝑓⁡(𝑔⁡(𝑥)).

Exercise 1.4.26

ℎ⁡(𝑥) =(𝑥+2)2

Exercise 1.4.27

ℎ⁡(𝑥) =(𝑥−5)3

Answer:

sample: 𝑓⁡(𝑥) =𝑥3

𝑔⁡(𝑥) =𝑥 −5

Exercise 1.4.28

ℎ⁡(𝑥) =3𝑥−5

Exercise 1.4.29

ℎ⁡(𝑥) =4(𝑥+2)2

Answer:

sample: 𝑓⁡(𝑥) =4𝑥

𝑔⁡(𝑥) =(𝑥+2)2

Exercise 1.4.30

ℎ⁡(𝑥) =4 +3√𝑥

Exercise 1.4.31

ℎ⁡(𝑥) =3√12⁢𝑥−3

Answer:

sample: 𝑓⁡(𝑥) =3√𝑥

𝑔⁡(𝑥) =12⁢𝑥−3

Exercise 1.4.32

ℎ⁡(𝑥) =1(3⁢𝑥2−4)−3

Exercise 1.4.33

ℎ⁡(𝑥) =4√3⁢𝑥−2𝑥+5

Answer:

sample: 𝑓⁡(𝑥) =4√𝑥

𝑔⁡(𝑥) =3⁢𝑥−2𝑥+5

Exercise 1.4.34

ℎ⁡(𝑥) =(8+𝑥38−𝑥3)4

Exercise 1.4.35

ℎ⁡(𝑥) =√2⁢𝑥+6

Answer:

sample: 𝑓⁡(𝑥) =√𝑥

𝑔⁡(𝑥) =2⁢𝑥 +6

Exercise 1.4.36

ℎ⁡(𝑥) =(5⁢𝑥−1)3

Exercise 1.4.37

ℎ⁡(𝑥) =3√𝑥−1

Answer:

sample: 𝑓⁡(𝑥) =3√𝑥

𝑔⁡(𝑥) =(𝑥 −1)

Exercise 1.4.38

ℎ⁡(𝑥) =|𝑥2 +7|

Exercise 1.4.39

ℎ⁡(𝑥) =1(𝑥−2)3

Answer:

sample: 𝑓⁡(𝑥) =𝑥3
𝑔⁡(𝑥) =1𝑥−2

Exercise 1.4.40

ℎ⁡(𝑥) =(12⁢𝑥−3)2

Exercise 1.4.41

ℎ⁡(𝑥) =√2⁢𝑥−13⁢𝑥+4

Answer:

sample: 𝑓⁡(𝑥) =√𝑥
𝑔⁡(𝑥) =2⁢𝑥−13⁢𝑥+4

Graphical

For the following exercises, use the graphs of 𝑓,shown in Figure 1.4.6, and 𝑔,shown in Figure 1.4.7, to evaluate the expressions.

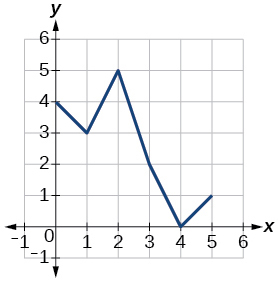
Figure 1.4.6: Graph of a function.

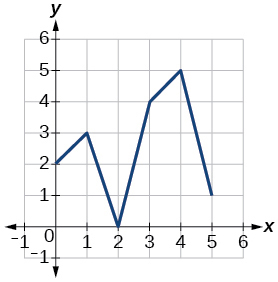
Figure 1.4.7: Graph of a function.

Exercise 1.4.42

𝑓⁡(𝑔⁡(3))

Exercise 1.4.43

𝑓⁡(𝑔⁡(1))

Answer:

2

Exercise 1.4.44

𝑔⁡(𝑓⁡(1))

Exercise 1.4.45

𝑔⁡(𝑓⁡(0))

Answer:

5

Exercise 1.4.46

𝑓⁡(𝑓⁡(5))

Exercise 1.4.47

𝑓⁡(𝑓⁡(4))

Answer:

4

Exercise 1.4.48

𝑔⁡(𝑔⁡(2))

Exercise 1.4.49

𝑔⁡(𝑔⁡(0))

Answer:

0

For the following exercises, use graphs of 𝑓⁡(𝑥),shown in Figure 1.4.8, 𝑔⁡(𝑥),shown in Figure 1.4.9, and ℎ⁡(𝑥),shown in Figure 1.4.10, to evaluate the expressions.

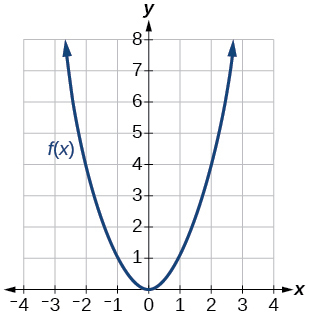
Figure 1.4.8: Graph of a parabola.

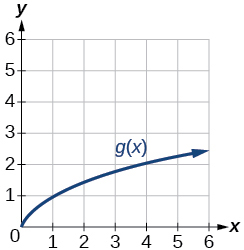
Figure 1.4.9: Graph of a square root function.

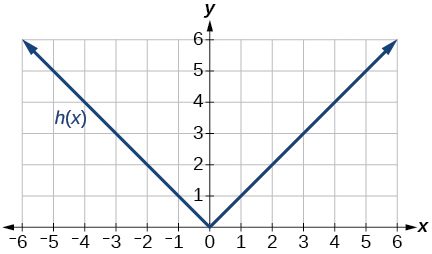
Figure 1.4.10: Graph of an absolute value function.

Exercise 1.4.50

𝑔⁡(𝑓⁡(1))

Exercise 1.4.51

𝑔⁡(𝑓⁡(2))

Answer:

2

Exercise 1.4.52

𝑓⁡(𝑔⁡(4))

Exercise 1.4.53

𝑓⁡(𝑔⁡(1))

Answer:

1

Exercise 1.4.54

𝑓⁡(ℎ⁡(2))

Exercise 1.4.55

ℎ⁡(𝑓⁡(2))

Answer:

4

Exercise 1.4.56

𝑓⁡(𝑔⁡(ℎ⁡(4)))

Exercise 1.4.57

𝑓⁡(𝑔⁡(𝑓⁡(−2)))

Answer:

4

Numeric

For the following exercises, use the function values for 𝑓 and 𝑔 shown in Table 1.4.3 to evaluate each expression.

𝑥	𝑓⁡(𝑥)	𝑔⁡(𝑥)
0	7	9
1	6	5
2	5	6
3	8	2
4	4	1
5	0	8
6	2	7
7	1	3
8	9	4
9	3	0

Table 1.4.3

Exercise 1.4.58

𝑓⁡(𝑔⁡(8))

Exercise 1.4.59

𝑓⁡(𝑔⁡(5))

Answer:

9

Exercise 1.4.60

𝑔⁡(𝑓⁡(5))

Exercise 1.4.61

𝑔⁡(𝑓⁡(3))

Answer:

4

Exercise 1.4.62

𝑓⁡(𝑓⁡(4))

Exercise 1.4.63

𝑓⁡(𝑓⁡(1))

Answer:

2

Exercise 1.4.64

𝑔⁡(𝑔⁡(2))

Exercise 1.4.65

𝑔⁡(𝑔⁡(6))

Answer:

3

For the following exercises, use the function values for 𝑓 and 𝑔 shown in Table 1.4.4 to evaluate the expressions.

𝑥	𝑓⁡(𝑥)	𝑔⁡(𝑥)
-3	11	-8
-2	9	-3
-1	7	0
0	5	1
1	3	0
2	1	-3
3	-1	-8

Exercise 1.4.66

(𝑓 ∘𝑔)⁡(1)

Exercise 1.4.67

(𝑓 ∘𝑔)⁡(2)

Answer:

11

Exercise 1.4.68

(𝑔 ∘𝑓)⁡(2)

Exercise 1.4.69

(𝑔 ∘𝑓)⁡(3)

Answer:

0

Exercise 1.4.70

(𝑔 ∘𝑔)⁡(1)

Exercise 1.4.71

(𝑓 ∘𝑓)⁡(3)

Answer:

7

For the following exercises, use each pair of functions to find 𝑓⁡(𝑔⁡(0)) and 𝑔⁡(𝑓⁡(0)).

Exercise 1.4.72

𝑓⁡(𝑥) =4⁢𝑥 +8, 𝑔⁡(𝑥) =7 −𝑥2

Exercise 1.4.73

𝑓⁡(𝑥) =5⁢𝑥 +7, 𝑔⁡(𝑥) =4 −2⁢𝑥2

Answer:

𝑓⁡(𝑔⁡(0)) =27, 𝑔⁡(𝑓⁡(0)) =−94

Exercise 1.4.74

𝑓⁡(𝑥) =√𝑥+4, 𝑔⁡(𝑥) =12 −𝑥3

Exercise 1.4.75

𝑓⁡(𝑥) =1𝑥+2, 𝑔⁡(𝑥) =4⁢𝑥 +3

Answer:

𝑓⁡(𝑔⁡(0)) =15, 𝑔⁡(𝑓⁡(0)) =5

For the following exercises, use the functions 𝑓⁡(𝑥) =2⁢𝑥2 +1 and 𝑔⁡(𝑥) =3⁢𝑥 +5 to evaluate or find the composite function as indicated.

Exercise 1.4.76

𝑓⁡(𝑔⁡(2))

Exercise 1.4.77

𝑓⁡(𝑔⁡(𝑥))

Answer:

18⁢𝑥2 +60⁢𝑥 +51

Exercise 1.4.78

𝑔⁡(𝑓⁡(−3))

Exercise 1.4.79

(𝑔 ∘𝑔)⁡(𝑥)

Answer:

𝑔 ∘𝑔⁡(𝑥) =9⁢𝑥 +20

Extensions

For the following exercises, use 𝑓⁡(𝑥) =𝑥3 +1 and 𝑔⁡(𝑥) =3√𝑥−1.

Exercise 1.4.80

Find (𝑓 ∘𝑔)⁡(𝑥) and (𝑔 ∘𝑓)⁡(𝑥). Compare the two answers.

Exercise 1.4.81

Find (𝑓 ∘𝑔)⁡(2) and (𝑔 ∘𝑓)⁡(2).

Answer:

2

Exercise 1.4.82

What is the domain of (𝑔 ∘𝑓)⁡(𝑥)?

Exercise 1.4.83

What is the domain of (𝑓 ∘𝑔)⁡(𝑥)?

Answer:

(−∞,∞)

Exercise 1.4.84

Let 𝑓⁡(𝑥) =1𝑥.

a. Find (𝑓 ∘𝑓)⁡(𝑥).

b. Is (𝑓 ∘𝑓)⁡(𝑥) for any function 𝑓 the same result as the answer to part (a) for any function? Explain.

For the following exercises, let 𝐹⁡(𝑥) =(𝑥+1)5, 𝑓⁡(𝑥) =𝑥5, and 𝑔⁡(𝑥) =𝑥 +1.

Exercise 1.4.85

True or False: (𝑔 ∘𝑓)⁡(𝑥) =𝐹⁡(𝑥).

Answer:

False

Exercise 1.4.86

True or False: (𝑓 ∘𝑔)⁡(𝑥) =𝐹⁡(𝑥).

For the following exercises, find the composition when 𝑓⁡(𝑥) =𝑥2 +2 for all 𝑥 ≥0 and 𝑔⁡(𝑥) =√𝑥−2.

Exercise 1.4.87

(𝑓 ∘𝑔)⁡(6); (𝑔 ∘𝑓)⁡(6)

Answer:

(𝑓 ∘𝑔)⁡(6) =6 , (𝑔 ∘𝑓)⁡(6) =6

Exercise 1.4.88

(𝑔 ∘𝑓)⁡(𝑎); (𝑓 ∘𝑔)⁡(𝑎)

Exercise 1.4.89

(𝑓 ∘𝑔)⁡(11); (𝑔 ∘𝑓)⁡(11)

Answer:

(𝑓 ∘𝑔)⁡(11) =11 , (𝑔 ∘𝑓)⁡(11) =11

Real-World Applications

Exercise 1.4.90

The function 𝐷⁡(𝑝) gives the number of items that will be demanded when the price is 𝑝. The production cost 𝐶⁡(𝑥) is the cost of producing 𝑥 items. To determine the cost of production when the price is $6, you would do which of the following?

a. Evaluate 𝐷⁡(𝐶⁡(6)).
b. Evaluate 𝐶⁡(𝐷⁡(6)).
c. Solve 𝐷⁡(𝐶⁡(𝑥)) =6.
d. Solve 𝐶⁡(𝐷⁡(𝑝)) =6.

Exercise 1.4.91

The function 𝐴⁡(𝑑) gives the pain level on a scale of 0 to 10 experienced by a patient with 𝑑 milligrams of a pain-reducing drug in her system. The milligrams of the drug in the patient’s system after 𝑡 minutes is modeled by 𝑚⁡(𝑡). Which of the following would you do in order to determine when the patient will be at a pain level of 4?

a. Evaluate 𝐴⁡(𝑚⁡(4)).
b. Evaluate 𝑚⁡(𝐴⁡(4)).
c. Solve 𝐴⁡(𝑚⁡(𝑡)) =4.
d. Solve 𝑚⁡(𝐴⁡(𝑑)) =4.

Answer:

c

Exercise 1.4.92

A store offers customers a 30% discount on the price x of selected items. Then, the store takes off an additional 15% at the cash register. Write a price function 𝑃⁡(𝑥) that computes the final price of the item in terms of the original price 𝑥. (Hint: Use function composition to find your answer.)

Exercise 1.4.93

A rain drop hitting a lake makes a circular ripple. If the radius, in inches, grows as a function of time in minutes according to 𝑟⁡(𝑡) =25⁢√𝑡+2, find the area of the ripple as a function of time. Find the area of the ripple at 𝑡 =2.

Answer:

𝐴⁡(𝑡) =𝜋⁢(25⁢√𝑡+2)2 and 𝐴⁡(2) =𝜋⁢(25⁢√4)2 =2500⁢𝜋 square inches

Exercise 1.4.94

A forest fire leaves behind an area of grass burned in an expanding circular pattern. If the radius of the circle of burning grass is increasing with time according to the formula 𝑟⁡(𝑡) =2⁢𝑡 +1, express the area burned as a function of time, 𝑡 (minutes).

Exercise 1.4.95

Use the function you found in the previous exercise to find the total area burned after 5 minutes.

Answer:

𝐴⁡(5) =𝜋⁢(2⁢(5) +1)⁢2 =121⁢𝜋 square units

Exercise 1.4.96

The radius 𝑟, in inches, of a spherical balloon is related to the volume, 𝑉, by 𝑟⁡(𝑉) =3√3⁢𝑉4⁢𝜋. Air is pumped into the balloon, so the volume after 𝑡 seconds is given by 𝑉⁡(𝑡) =10 +20⁢𝑡.

a. Find the composite function 𝑟⁡(𝑉⁡(𝑡)).

b. Find the exact time when the radius reaches 10 inches.

Exercise 1.4.97

The number of bacteria in a refrigerated food product is given by 𝑁⁡(𝑇) =23⁢𝑇2 −56⁢𝑇 +1, 3 <𝑇 <33, where 𝑇 is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by 𝑇⁡(𝑡) =5⁢𝑡 +1.5, where 𝑡 is the time in hours.

Find the composite function 𝑁⁡(𝑇⁡(𝑡)).
Find the time (round to two decimal places) when the bacteria count reaches 6752.

Answer:

a. 𝑁⁡(𝑇⁡(𝑡)) =23⁢(5⁢𝑡+1.5)2 −56⁢(5⁢𝑡 +1.5) +1
b. 3.38 hours