3.2E: Exercises for Section 3.2
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 8, find
1)
2)
- Answer
3)
4)
- Answer
5)
6)
- Answer
7)
- Answer
8)
In exercises 9 - 12, find the equation of the tangent line
9) [T]
10) [T]
- Answer
-
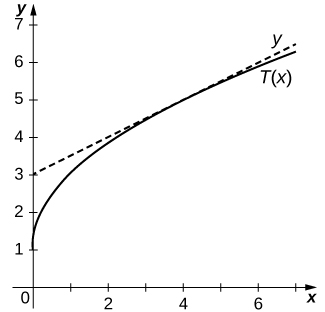
11) [T]
12) [T]
- Answer
-
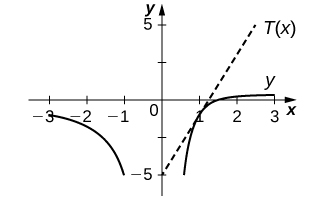
In exercise 13, assume that
13)
In exercises 14-17,
a) evaluate
b) graph the function
14) [T]
- Answer
-
a. 23
b.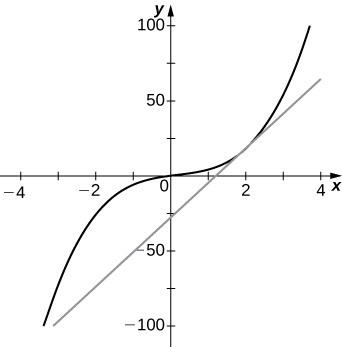
15) [T]
16) [T]
- Answer
-
a.
b.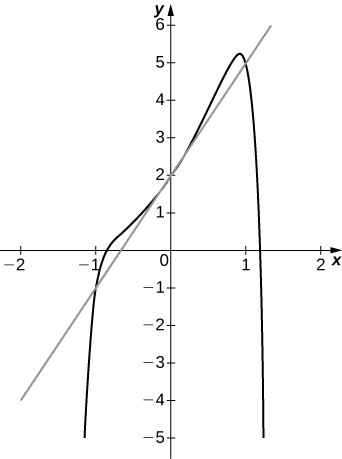
17) [T]
18) Find the equation of the tangent line to the graph of
- Answer
19) Find the equation of the tangent line to the graph of
20) Find the point on the graph of
21) Find the equation of the line passing through the point
- Answer
22) Determine all points on the graph of
a. horizontal
b. −1.
23) Find a quadratic polynomial such that
- Answer
24) A car driving along a freeway with traffic has traveled
a. Determine the time in seconds when the velocity of the car is 0.
b. Determine the acceleration of the car when the velocity is 0.
25) The population in millions of arctic flounder in the Atlantic Ocean is modeled by the function
a. Determine the initial flounder population.
b. Determine
26) A book publisher has a cost function given by
27) [T] According to Newton’s law of universal gravitation, the force
a. Suppose that
b. Find the rate of change of force
- Answer
- a.
b.
Contributors and Attributions
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

