9.5: Counting

Counting? You already know how to count or you wouldn't be taking a college-level math class, right? Well yes, but what we'll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don't want to do this.

Basic Counting

We will start, however, with some more reasonable sorts of counting problems in order to develop the ideas that we will soon need.

Example 21

Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pizza). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?

Solution

Solution 1: One way to solve this problem would be to systematically list each possible meal:

$\begin{array}{lll} \text{soup + hamburger} & \text{soup + sandwich} & \text{soup + quiche} \\ \text{soup + fajita} & \text{soup + pizza} & \text{salad + hamburger} \\ \text{salad + sandwich} & \text{salad + quiche} & \text{salad + fajita} \\ \text{salad + pizza} & \text{breadsticks + hamburger} & \text{breadsticks + sandwich} \\ \text{breadsticks + quiche} & \text{breadsticks + fajita} & \text{breadsticks + pizza} \end{array}$

Assuming that we did this systematically and that we neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus you could go to the restaurant 15 nights in a row and have a different meal each night.

Solution 2: Another way to solve this problem would be to list all the possibilities in a table:

$\begin{array}{|l|l|l|l|l|l|} \hline & \textbf { hamburger } & \textbf { sandwich } & \textbf { quiche } & \textbf { fajita } & \textbf { pizza } \\ \hline \textbf { soup } & \text { Soup + burger } & & & & \\ \hline \textbf { salad } & \text { Salad + burger } & & & & \\ \hline \textbf { bread } & e t c . & & & & \\ \hline \end{array}$

In each of the cells in the table we could list the corresponding meal: soup + hamburger in the upper left corner, salad + hamburger below it, etc. But if we didn't really care what the possible meals are, only how many possible meals there are, we could just count the number of cells and arrive at an answer of 15, which matches our answer from the first solution. (It's always good when you solve a problem two different ways and get the same answer!)

Solution 3: We already have two perfectly good solutions. Why do we need a third? The first method was not very systematic, and we might easily have made an omission. The second method was better, but suppose that in addition to the appetizer and the main course we further complicated the problem by adding desserts to the menu: we've used the rows of the table for the appetizers and the columns for the main courses—where will the desserts go? We would need a third dimension, and since drawing 3-D tables on a 2-D page or computer screen isn't terribly easy, we need a better way in case we have three categories to choose form instead of just two.

So, back to the problem in the example. What else can we do? Let's draw a tree diagram:

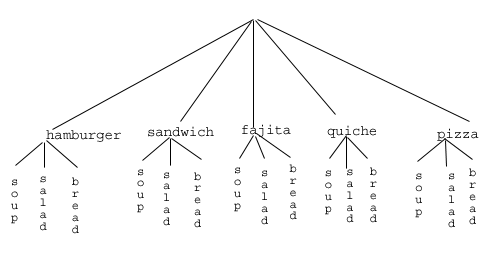
This is called a "tree" diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15.

If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.

OK, so now we know how to count possibilities using tables and tree diagrams. These methods will continue to be useful in certain cases, but imagine a game where you have two decks of cards (with 52 cards in each deck) and you select one card from each deck. Would you really want to draw a table or tree diagram to determine the number of outcomes of this game?

Let's go back to the previous example that involved selecting a meal from three appetizers and five main courses, and look at the second solution that used a table. Notice that one way to count the number of possible meals is simply to number each of the appropriate cells in the table, as we have done above. But another way to count the number of cells in the table would be multiply the number of rows (3) by the number of columns (5) to get 15. Notice that we could have arrived at the same result without making a table at all by simply multiplying the number of choices for the appetizer (3) by the number of choices for the main course (5). We generalize this technique as the basic counting rule:

Basic Counting Rule

If we are asked to choose one item from each of two separate categories where there are $m$ items in the first category and $n$ items in the second category, then the total number of available choices is $m \cdot n$

This is sometimes called the multiplication rule for probabilities.

Example 22

There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter?

Solution

There are 21 choices from the first category and 18 for the second, so there are $21 \cdot 18 = 378$ possibilities.

The Basic Counting Rule can be extended when there are more than two categories by applying it repeatedly, as we see in the next example.

Example 23

Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?

Solution

There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are $3 \cdot 5 \cdot 2=30$ possibilities.

Example 24

A quiz consists of 3 true-or-false questions. In how many ways can a student answer the quiz?

Solution

There are 3 questions. Each question has 2 possible answers (true or false), so the quiz may be answered in $2 \cdot 2 \cdot 2=8$ different ways. Recall that another way to write $2 \cdot 2 \cdot 2$ is $2^{3}$ which is much more compact.

Try it Now 6

Suppose at a particular restaurant you have eight choices for an appetizer, eleven choices for a main course and five choices for dessert. If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?

Answer

$8 \cdot 11 \cdot 5=440$ menu combinations

Permutations

In this section we will develop an even faster way to solve some of the problems we have already learned to solve by other means. Let's start with a couple examples.

Example 25

How many different ways can the letters of the word MATH be rearranged to form a four-letter code word?

Solution

This problem is a bit different. Instead of choosing one item from each of several different categories, we are repeatedly choosing items from the same category (the category is: the letters of the word MATH) and each time we choose an item we do not replace it, so there is one fewer choice at the next stage: we have 4 choices for the first letter (say we choose A), then 3 choices for the second (M, T and H; say we choose H), then 2 choices for the next letter (M and T; say we choose M) and only one choice at the last stage (T). Thus there are $4 \cdot 3 \cdot 2 \cdot 1=24$ ways to spell a code worth with the letters MATH.

In this example, we needed to calculate $n \cdot(n-1) \cdot(n-2) \cdots 3 \cdot 2 \cdot 1$. This calculation shows up often in mathematics, and is called the factorial, and is notated $n$!

Factorial

$n !=n \cdot(n-1) \cdot(n-2) \cdots 3 \cdot 2 \cdot 1$

Example 26

How many ways can five different door prizes be distributed among five people?

Solution

There are 5 choices of prize for the first person, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be $5 !=5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=120$ ways.

Now we will consider some slightly different examples.

Example 27

A charity benefit is attended by 25 people and three gift certificates are given away as door prizes: one gift certificate is in the amount of $100, the second is worth $25 and the third is worth $10. Assuming that no person receives more than one prize, how many different ways can the three gift certificates be awarded?

Solution

Using the Basic Counting Rule, there are 25 choices for the person who receives the $\$ 100$ certificate, 24 remaining choices for the $\$ 25$ certificate and 23 choices for the $\$ 10$ certificate, so there are $25 \cdot 24 \cdot 23=13,800$ ways in which the prizes can be awarded.

Example 28

Eight sprinters have made it to the Olympic finals in the 100-meter race. In how many different ways can the gold, silver and bronze medals be awarded?

Solution

Using the Basic Counting Rule, there are 8 choices for the gold medal winner, 7 remaining choices for the silver, and 6 for the bronze, so there are $8 \cdot 7 \cdot 6=336$ ways the three medals can be awarded to the 8 runners.

Note that in these preceding examples, the gift certificates and the Olympic medals were awarded without replacement; that is, once we have chosen a winner of the first door prize or the gold medal, they are not eligible for the other prizes. Thus, at each succeeding stage of the solution there is one fewer choice (25, then 24, then 23 in the first example; 8, then 7, then 6 in the second). Contrast this with the situation of a multiple choice test, where there might be five possible answers — A, B, C, D or E — for each question on the test.

Note also that the order of selection was important in each example: for the three door prizes, being chosen first means that you receive substantially more money; in the Olympics example, coming in first means that you get the gold medal instead of the silver or bronze. In each case, if we had chosen the same three people in a different order there might have been a different person who received the $100 prize, or a different goldmedalist. (Contrast this with the situation where we might draw three names out of a hat to each receive a $10 gift certificate; in this case the order of selection is not important since each of the three people receive the same prize. Situations where the order is not important will be discussed in the next section.)

We can generalize the situation in the two examples above to any problem without replacement where the order of selection is important. If we are arranging in order $r$ items out of $n$ possibilities (instead of 3 out of 25 or 3 out of 8 as in the previous examples), the number of possible arrangements will be given by

$n \cdot(n-1) \cdot(n-2) \cdots(n-r+1)$

If you don't see why $(n-r+1)$ is the right number to use for the last factor, just think back to the first example in this section, where we calculated $25 \cdot 24 \cdot 23$ to get $13,800 .$ In this case $n=25$ and $r=3,$ so $n-r+1=25-3+1=23,$ which is exactly the right number for the final factor.

Now, why would we want to use this complicated formula when it's actually easier to use the Basic Counting Rule, as we did in the first two examples? Well, we won't actually use this formula all that often, we only developed it so that we could attach a special notation and a special definition to this situation where we are choosing $r$ items out of $n$ possibilities without replacement and where the order of selection is important. In this situation we write:

Permutations

$_{n} P_{r}=n \cdot(n-1) \cdot(n-2) \cdots(n-r+1)$

We say that there are $_{n} P_{r}$ permutations of size $r$ that may be selected from among $n$ choices without replacement when order matters.

It turns out that we can express this result more simply using factorials.

$_{n} P_{r}=\frac{n !}{(n-r) !}$

In practicality, we usually use technology rather than factorials or repeated multiplication to compute permutations.

Example 29

I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this?

Solution

Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are $_9 P_{4}=9 \cdot 8 \cdot 7 \cdot 6=3,024$ permutations.

Example 30

How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization?

Solution

We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is $_{16} P_{4}=16 \cdot 15 \cdot 14 \cdot 13=43,680$.

Try it Now 7

How many 5 character passwords can be made using the letters A through Z

1. if repeats are allowed
2. if no repeats are allowed

Answer

There are 26 characters.

1. $26^{5}=11,881,376$.
2. ${26} \mathrm{P}_{5}=26 \cdot 25 \cdot 24 \cdot 23 \cdot 22=7,893,600$

Combinations

In the previous section we considered the situation where we chose $r$ items out of $n$ possibilities without replacement and where the order of selection was important. We now consider a similar situation in which the order of selection is not important.

Example 31

A charity benefit is attended by 25 people at which three $50 gift certificates are given away as door prizes. Assuming no person receives more than one prize, how many different ways can the gift certificates be awarded?

Solution

Using the Basic Counting Rule, there are 25 choices for the first person, 24 remaining choices for the second person and 23 for the third, so there are $25 \cdot 24 \cdot 23=13,800$ ways to choose three people. Suppose for a moment that Abe is chosen first, Bea second and Cindy third; this is one of the 13,800 possible outcomes. Another way to award the prizes would be to choose Abe first, Cindy second and Bea third; this is another of the 13,800 possible outcomes. But either way Abe, Bea and Cindy each get $50, so it doesn't really matter the order in which we select them. In how many different orders can Abe, Bea and Cindy be selected? It turns out there are 6:

ABC ACB BAC BCA CAB CBA

How can we be sure that we have counted them all? We are really just choosing 3 people out of 3, so there are $3 \cdot 2 \cdot 1=6$ ways to do this; we didn't really need to list them all, we can just use permutations!

So, out of the 13,800 ways to select 3 people out of 25, six of them involve Abe, Bea and Cindy. The same argument works for any other group of three people (say Abe, Bea and David or Frank, Gloria and Hildy) so each three-person group is counted six times. Thus the 13,800 figure is six times too big. The number of distinct three-person groups will be $\frac{13,800}{6} = 2300$.

We can generalize the situation in this example above to any problem of choosing a collection of items without replacement where the order of selection is not important. If we are choosing $r$ items out of $n$ possibilities (instead of 3 out of 25 as in the previous examples), the number of possible choices will be given by , and we could use this formula for computation. However this situation arises so frequently that we attach a special notation and a special definition to this situation where we are choosing $r$ items out of $n$ possibilities without replacement where the order of selection is not important.

Combinations

$_{n} C_{r}=\frac{_n P_{r}}{r P_{r}}$

We say that there are $_{n} C_{r}$ combinations of size $r$ that may be selected from among $n$ choices without replacement where order doesn’t matter.

We can also write the combinations formula in terms of factorials:

$_{n} C_{r}=\frac{n !}{(n-r) ! r !}$

Example 32

A group of four students is to be chosen from a 35-member class to represent the class on the student council. How many ways can this be done?

Solution

Since we are choosing 4 people out of 35 without replacement where the order of selection is not important there are = $_{35} C_{4}=\frac{35 \cdot 34 \cdot 33 \cdot 32}{4 \cdot 3 \cdot 2 \cdot 1}=52,360$ combinations.

Try it Now 8

The United States Senate Appropriations Committee consists of 29 members; the Defense Subcommittee of the Appropriations Committee consists of 19 members. Disregarding party affiliation or any special seats on the Subcommittee, how many different 19-member subcommittees may be chosen from among the 29 Senators on the Appropriations Committee?

Answer

Order does not matter. $_{29} \mathrm{C}_{19}=20,030,010$ possible subcommittees

In the preceding Try it Now problem we assumed that the 19 members of the Defense Subcommittee were chosen without regard to party affiliation. In reality this would never happen: if Republicans are in the majority they would never let a majority of Democrats sit on (and thus control) any subcommittee. (The same of course would be true if the Democrats were in control.) So let's consider the problem again, in a slightly more complicated form:

Example 33

The United States Senate Appropriations Committee consists of 29 members, 15 Republicans and 14 Democrats. The Defense Subcommittee consists of 19 members, 10 Republicans and 9 Democrats. How many different ways can the members of the Defense Subcommittee be chosen from among the 29 Senators on the Appropriations Committee?

Solution

In this case we need to choose 10 of the 15 Republicans and 9 of the 14 Democrats. There are $_{15} C_{10}=3003$ ways to choose the 10 Republicans and $_{14} C_{9}=2002$ ways to choose the 9 Democrats. But now what? How do we finish the problem?

Suppose we listed all of the possible 10-member Republican groups on 3003 slips of red paper and all of the possible 9-member Democratic groups on 2002 slips of blue paper. How many ways can we choose one red slip and one blue slip? This is a job for the Basic Counting Rule! We are simply making one choice from the first category and one choice from the second category, just like in the restaurant menu problems from earlier.

There must be $3003 \cdot 2002=6,012,006$ possible ways of selecting the members of the Defense Subcommittee.

Probability using Permutations and Combinations

We can use permutations and combinations to help us answer more complex probability questions

Example 34

A 4 digit PIN number is selected. What is the probability that there are no repeated digits?

Solution

There are $10 \text { possible values for each digit of the PIN (namely: } 0,1,2,3,4,5,6,7,8,9),$ so there are $10 \cdot 10 \cdot 10 \cdot 10=10^{4}=10000$ total possible PIN numbers.

To have no repeated digits, all four digits would have to be different, which is selecting without replacement. We could either compute 10 \cdot 9 \cdot 8 \cdot 7, or notice that this is the same as the permutation $_{10} P_{4}=5040$.

The probability of no repeated digits is the number of 4 digit PIN numbers with no repeated digits divided by the total number of 4 digit PIN numbers. This probability is $\frac{_{10} P_{4}}{10^{4}}=\frac{5040}{10000}=0.504$

Example 35

In a certain state's lottery, 48 balls numbered 1 through 48 are placed in a machine and six of them are drawn at random. If the six numbers drawn match the numbers that a player had chosen, the player wins $1,000,000. In this lottery, the order the numbers are drawn in doesn’t matter. Compute the probability that you win the million-dollar prize if you purchase a single lottery ticket.

Solution

In order to compute the probability, we need to count the total number of ways six numbers can be drawn, and the number of ways the six numbers on the player’s ticket could match the six numbers drawn from the machine. Since there is no stipulation that the numbers be in any particular order, the number of possible outcomes of the lottery drawing is $_{48} C_{6}=12,271,512$. Of these possible outcomes, only one would match all six numbers on the player’s ticket, so the probability of winning the grand prize is:

$\frac{_6 C_{6}}{_{48} C_{6}}=\frac{1}{12271512} \approx 0.0000000815$

Example 36

In the state lottery from the previous example, if five of the six numbers drawn match the numbers that a player has chosen, the player wins a second prize of $1,000. Compute the probability that you win the second prize if you purchase a single lottery ticket.

Solution

As above, the number of possible outcomes of the lottery drawing is $_{48} C_{6}=12,271,512$. In order to win the second prize, five of the six numbers on the ticket must match five of the six winning numbers; in other words, we must have chosen five of the six winning numbers and one of the 42 losing numbers. The number of ways to choose 5 out of the 6 winning numbers is given by $_{6} C_{5}=6$ and the number of ways to choose 1 out of the 42 losing numbers is given by $_{42} C_{1}=42$. Thus the number of favorable outcomes is then given by the Basic Counting Rule: $_{6} C_{5} \cdot_{42} C_{1}=6 \cdot 42=252$. So the probability of winning the second prize is.

$\frac{\left(_{6} C_{5}\right)\left(_{42} C_{1}\right)}{_{48} C_{6}}=\frac{252}{12271512} \approx 0.0000205$

Try it Now 9

A multiple-choice question on an economics quiz contains 10 questions with five possible answers each. Compute the probability of randomly guessing the answers and getting 9 questions correct.

Answer

There are $5^{10}=9,765,625$ different ways the exam can be answered. There are 10 possible locations for the one missed question, and in each of those locations there are 4 wrong answers, so there are 40 ways the test could be answered with one wrong answer.

$\mathrm{P}(9 \text { answers correct })=\frac{40}{5^{10}} \approx 0.0000041$ chance

Example 37

Compute the probability of randomly drawing five cards from a deck and getting exactly one Ace.

Solution

In many card games (such as poker) the order in which the cards are drawn is not important (since the player may rearrange the cards in his hand any way he chooses); in the problems that follow, we will assume that this is the case unless otherwise stated. Thus we use combinations to compute the possible number of 5-card hands, $_{52} C_{5}$. This number will go in the denominator of our probability formula, since it is the number of possible outcomes.

For the numerator, we need the number of ways to draw one Ace and four other cards (none of them Aces) from the deck. Since there are four Aces and we want exactly one of them, there will be $_4 C_{1}$ ways to select one Ace; since there are 48 non-Aces and we want 4 of them, there will be $_{48} C_{4}$\) ways to select the four non-Aces. Now we use the Basic Counting Rule to calculate that there will be $_{4} C_{1} \cdot _{48} C_{4}$ ways to choose one ace and four non-Aces.

Putting this all together, we have

$P(\text {one Ace} )=\frac{\left(_{4} C_{1}\right)\left(_{48} C_{4}\right)}{_{52} C_{5}}=\frac{778320}{2598960} \approx 0.299$

Example 38

Compute the probability of randomly drawing five cards from a deck and getting exactly two Aces.

Solution

The solution is similar to the previous example, except now we are choosing 2 Aces out of 4 and 3 non-Aces out of 48; the denominator remains the same:

$P(\text {two Aces})=\frac{\left(_{4} C_{2}\right)\left(_{48} C_{3}\right)}{_{52} C_{5}}=\frac{103776}{2598960} \approx 0.0399$

It is useful to note that these card problems are remarkably similar to the lottery problems discussed earlier.

Try it Now 10

Compute the probability of randomly drawing five cards from a deck of cards and getting three Aces and two Kings.

Answer

$P(\text {three Aces and two Kings})=\frac{\left(_{4} C_{3}\right)\left(_{4} C_{2}\right)}{_{52} C_{5}}=\frac{24}{2598960} \approx 0.0000092$

Birthday Problem

Let's take a pause to consider a famous problem in probability theory:

Suppose you have a room full of 30 people. What is the probability that there is at least one shared birthday?

Take a guess at the answer to the above problem. Was your guess fairly low, like around 10%? That seems to be the intuitive answer ($\frac{30}{365}$, perhaps?). Let's see if we should listen to our intuition. Let's start with a simpler problem, however.

Example 39

Suppose three people are in a room. What is the probability that there is at least one shared birthday among these three people?

Solution

There are a lot of ways there could be at least one shared birthday. Fortunately there is an easier way. We ask ourselves “What is the alternative to having at least one shared birthday?” In this case, the alternative is that there are no shared birthdays. In other words, the alternative to “at least one” is having none. In other words, since this is a complementary event,

$P(\text {at least one})=1-P(\text {none})$

We will start, then, by computing the probability that there is no shared birthday. Let's imagine that you are one of these three people. Your birthday can be anything without conflict, so there are 365 choices out of 365 for your birthday. What is the probability that the second person does not share your birthday? There are 365 days in the year (let's ignore leap years) and removing your birthday from contention, there are 364 choices that will guarantee that you do not share a birthday with this person, so the probability that the second person does not share your birthday is $\frac{364}{365}$. Now we move to the third person. What is the probability that this third person does not have the same birthday as either you or the second person? There are 363 days that will not duplicate your birthday or the second person's, so the probability that the third person does not share a birthday with the first two is $\frac{363}{365}$.

We want the second person not to share a birthday with you and the third person not to share a birthday with the first two people, so we use the multiplication rule:

$P(\text {no shared birthday})=\frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \approx 0.9918$

and then subtract from 1 to get

$P(\text {shared birthday})=1-P(\text {no shared birthday})=1-0.9918=0.0082$.

This is a pretty small number, so maybe it makes sense that the answer to our original problem will be small. Let's make our group a bit bigger.

Example 40

Suppose five people are in a room. What is the probability that there is at least one shared birthday among these five people?

Solution

Continuing the pattern of the previous example, the answer should be

$P(\text {shared birthday})=1-\frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \frac{362}{365} \cdot \frac{361}{365} \approx 0.0271$

Note that we could rewrite this more compactly as

$P(\text {shared birthday})=1-\frac{_{365}P_5}{365^{5}} \approx 0.0271$

which makes it a bit easier to type into a calculator or computer, and which suggests a nice formula as we continue to expand the population of our group.

Example 41

Suppose 30 people are in a room. What is the probability that there is at least one shared birthday among these 30 people?

Solution

Here we can calculate

$P(\text { shared birthday })=1-\frac{_{365}P_{30}}{365^{30}} \approx 0.706$

which gives us the surprising result that when you are in a room with 30 people there is a 70% chance that there will be at least one shared birthday!

If you like to bet, and if you can convince 30 people to reveal their birthdays, you might be able to win some money by betting a friend that there will be at least two people with the same birthday in the room anytime you are in a room of 30 or more people. (Of course, you would need to make sure your friend hasn't studied probability!) You wouldn't be guaranteed to win, but you should win more than half the time.

This is one of many results in probability theory that is counterintuitive; that is, it goes against our gut instincts. If you still don't believe the math, you can carry out a simulation. Just so you won't have to go around rounding up groups of 30 people, someone has kindly developed a Java applet so that you can conduct a computer simulation. Go to this web page: http://statweb.stanford.edu/~susan/surprise/Birthday.html, and once the applet has loaded, select 30 birthdays and then keep clicking Start and Reset. If you keep track of the number of times that there is a repeated birthday, you should get a repeated birthday about 7 out of every 10 times you run the simulation.

Try it Now 11

Suppose 10 people are in a room. What is the probability that there is at least one shared birthday among these 10 people?

Answer

$P(\text {shared birthday})=1-\frac{_{365}P_{10}}{365^{10}} \approx 0.117$