1.2.1: Linear Expressions
- Page ID
- 98979
By the end of this section, you will be able to:
- Recognize a linear expression
- Simplify sums and differences of linear expressions
- Evaluate a linear expression for any value of the variable
Before we get started, take this readiness quiz.
1. Evaluate \(5(-1)−4\).
2. Evaluate \(3(4)−2(-3)\).
3. Evaluate \(-3(-2)+2(-1)-5(2)-3(-3)\).
Linear Expressions with One Variable
An expression that can be written as
\(A x+B\)
with \(A\) and \(B\) numbers, is called a linear expression (with one variable), or more specifically, a linear expression in \(x\). \(Ax\) and \(B\) are called terms. \(A\) is called the coefficient of \(x\) and \(B\) is called the constant coefficient.
Decide if the following are linear expressions. If so, identify \(A\) and \(B\) such that \(Ax+B\) is a linear expression.
a. \(\dfrac{2}{3}x-4\)
b. \(3\)
c. \(x\cdot x-2x\)
Solution
a. \(\dfrac{2}{3}x-4 =\dfrac{2}{3}x+(-4)\) is linear with \(A=\dfrac{2}{3}\) and \(B=-4\).
b. \(3=0\cdot x + 3\) is linear with \(A=0\) and \(B=3\).
c. \(x\cdot x-2x\) is not linear because it is not of the form \(Ax+B\) where \(A\) and \(B\) are numbers.
Decide if the following are linear expressions. If so, identify \(A\) and \(B\) such that \(Ax+B\) is a linear expression.
a. \(-\dfrac{3}{4}x\)
b. \(4-2x\)
c. \(x\cdot x\cdot x-2x\)
- Answer
-
a. Yes, \(A=-\dfrac{3}{4}\) and \(B=0\).
b. Yes, \(A=-2\) and \(B=4\).
c. No.
We are interested in such expressions because they occur frequently in applications. The one we will concern ourselves with at this time is if \(x\) represents some variety of numbers. For example, suppose we are interested in constructing a fenced region that has as one side a preexisting wall and the length of the region is 2 less than the width. Then we don't know what we want the width to be, so we call it \(x\) (we could call it something else if we wanted) and then we can express the length of fencing we need as \(3x+(-2)\). Now we can easily find the length of fence needed for various widths.
We will now treat this expression more abstractly (outside the context of the application above). To arrive at the expression \(3x+(-2)\) we multiply a variable \(x\) (an unknown quantity which we call '\(x\)') by the number \(3\) and then add another number \(-2\). We can evaluate this expression for different values of \(x\):
| Values of \(x\) | Evaluating \(3x+(-2)\) at \(x\) |
|---|---|
| \(x=2\) |
\(\begin{align*} &\;3x+(-2) \\= &\; 3(2)+(-2)\\= &\; 6+(-2)\\= &\; 4\end{align*}\) |
| \(x=-1\) |
\(\begin{align*} &\;3x+(-2)\\= &\;3(-1)+(-2)\\= &\;-3+(-2)\\= &\;-5\end{align*}\) |
| \(x=\dfrac{1}{2}\) |
\(\begin{align*} &\;3x+(-2)\\= &\;3\cdot\dfrac12+(-2)\\= &\;\dfrac32+(-2)\\=&\;\dfrac32+\left(-\dfrac42\right)\\= &\;-\dfrac12\end{align*}\) |
When we have a linear expression with a variable '\(x\)', any value for '\(x\)' is appropriate unless an application limits the meaningfulness of the expression. In the application above, only numbers greater than \(2\) make sense (why?).
We can add linear expressions and get another linear expression. To understand how this works you should treat \(x\) as a number:
\((3x-2)+(-2x+7)=3x+(-2x)+(-2)+7\) (because you can add in any order) means that you have 3 \(x\)'s and you add -2 \(x\)'s or, equivalently, you have 3 \(x\)'s and you take away \(2\) \(x\)'s, leaving you with one \(x\), and you have \(-2\) (units) and you add 7 (units) giving you 5. So the result is the sum \(x+5\).
As it is with numbers, to subtract we add the 'opposite', so we therefore need to know how to find the opposite of a linear expression. The opposite of \(A+Bx\) is \(-A+(-B)x\) because when you add these together you get zero: \(A+Bx+(-A)+(-B)x=A+(-A)+Bx+(-B)x=0\).
To demonstrate the process of subtraction, we consider the example: \((3x-2)-(-2x+7)\). The opposite of \(-2x+7\) is \(2x+(-7)=2x-7\) (you can check that adding these two expressions result in zero). So,
\(\begin{align*} &\;(3x-2)-(-2x+7)\\= &\;3x-2+2x-7\\= &\;3x+2x-2-7\\ = &\;5x-9.\end{align*}\)
The last equality is because \(3\) \(x\)'s plus 2 \(x\)'s gives you 5 \(x\)'s (for the same reason that having 3 dimes plus 2 dimes is the same as having 5 dimes). The process of arriving at the last equality is known as 'collecting like terms'.
This example also shows that not all linear expressions look like \(Ax+B\) but those that don't can be written so that any evaluation for the original and \(Ax+B\) for well chosen \(A\) and \(B\) is the same for any value of \(x\). For example:
| Values of \(x\) | Evaluating \((3x-2)-(-2x+7)\) at \(x\) | Evaluating \(5x-9\) at \(x\) |
|---|---|---|
| \(x=-2\) |
\(\begin{align*} &\;(3x-2)-(-2x+7)\\= &\;3(-2)-2-(-2(-2)+7)\\= &\;-6-2-(4+7)\\ = &\;-8-11\\=&\;-19\end{align*}\) |
\(\begin{align*}&\;5x-9\\= &\;5(-2)-9\\= &\;-10-9\\= &\;-19\end{align*}\) |
| \(x=3\) |
\(\begin{align*} &\;(3x-2)-(-2x+7)\\= &\;3(3)-2-(-2(3)+7)\\= &\;9-2-(-6+7)\\= &\;7-1\\= &\;6\end{align*}\) |
\(\begin{align*}&\;5x-9\\= &\;5(3)-9\\= &\;15-9\\= &\;6\end{align*}\) |
In fact, since we didn't rely on \(x\) being any particular value, we can check ANY value of \(x\) and find that the two expressions give the same answer. We say that \((3x-2)-(-2x+7)\) is equivalent to \(5x-9\). Since we can write \((3x-2)-(-2x+7)\) in the form \(Ax+B\), with \(A=5\) and \(B=9\), we see that \((3x-2)-(-2x+7)\) is linear.
In general, if we can operate with a number in a certain way, we can do the same with a variable.
We can multiply a linear expression by a number and still have a linear expression.
For example, \(2(2x+1)\) is \( 2x+1+2x+1=2(2x)+2(1)\). This is to say that we can 'distribute' the multiplication by 2 'over addition and subtraction', that is, we can multiply 2 by each term (understanding \(2x\) and \(1\) as the terms of the linear expression \(2x+1\)).
So,
\(2(2x+1)=2(2x)+2(1)=4x+2\)
which is of the form \(Ax+B\) where \(A=4\) and \(B=2\).
We noted above that \(2(2x+1)\) is \( 2x+1+2x+1=2(2x)+2(1)\). The analagous statement would be true if that 2 were replaced by any number!
For example \(7(2x+1)=7(2x)+7(1)\) and \(\dfrac83(2x+1)=\dfrac83(2x)+\dfrac83(1)\).
Show \(3(-3x+2)-2(x-1)+4x\) is a linear expression.
Solution
\(\begin{align*} &3(-3x+2)-2(x-1)+4x\\= &-9x+2+(-2)x+(-2)(-1)+4x\\= &-9x+(-2)x+4x+2+2\\ = &-11x+4\end{align*}\)
Since we have written this in the form \(Ax+B\) where \(A\) and \(B\) are numbers, we see this is a linear expression.
Show \(-2(3x-7)-5(-2x+3)+4(-x-1)\) is a linear expression.
- Answer
-
\(-5\)
Show \(-\dfrac23(3x-12)+\dfrac12(-2x+3)+(-x-\dfrac13)\) is a linear expression.
- Answer
-
\(-4x+\dfrac{19}{3}\)
We now consider some applications.
Write an expression that gives the perimeter of a square whose side is length \(x\). Use the expression to find the perimeter of a square with side lengths \(2 \;\mathrm{ cm}\).
Solution
First we draw and label a picture which represents the situation:
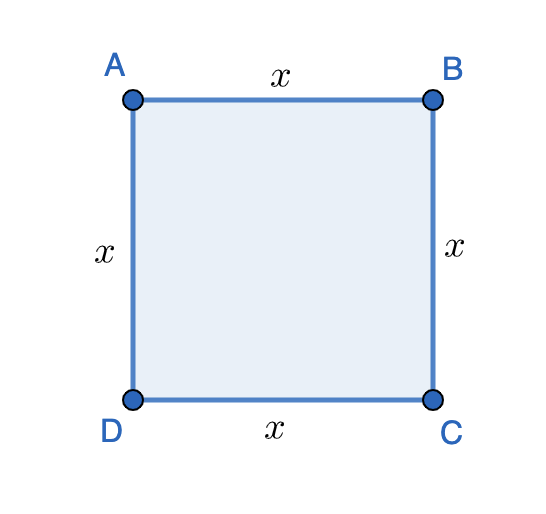
The perimeter is the distance around the square which in this case is \(x+x+x+x=4x\).
If \(x=2\;\mathrm{ cm}\). then the perimeter is \(4\cdot 2=8 \;\mathrm{ cm}\).
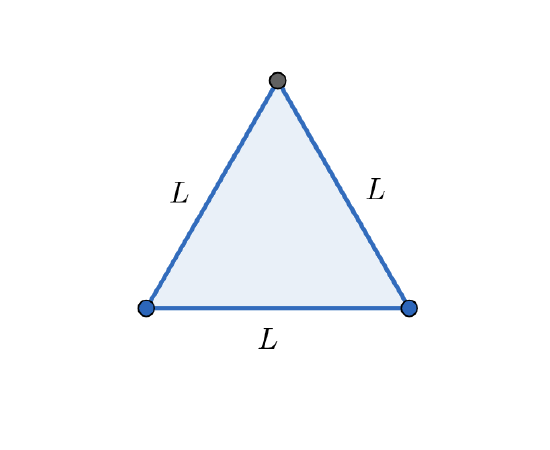
a. Give an expression for the perimeter of a equilateral triangle whose sides have length \(L\). Use the formula to find the perimeter of a triangle whose sides are length \(5 \;\mathrm{ft}\).
b. If a string has length \(L\) and we cut off \(5 \;\mathrm{in}\), what is the remaining length in terms of \(L\)? Use the formula to find the length remaining if we cut \(5 \;\mathrm{in}\) off a string of length \(7 \;\mathrm{in}\).
c. If we make a box of height \(x\), with no top, by cutting square corners from a \(30\;\mathrm{ in}\) in by \(30\;\mathrm{ in}\) piece or cardboard and folding them up what are the dimensions of the base of the box in terms of \(x\)? What is the biggest \(x\) can be?
- Answer
-
a. \(3L\); \(15 \mathrm{ ft}\)
b. \(L-5\); \(7-5=2 \mathrm{ in}\).
c. \(30-2x\); \(x\) must be smaller than \(15 \mathrm{ in}\).
Linear Expressions with Two Variables
Sometimes there is more than one unknown quantity or more than one quantity that has varying values. This leads us to consider the simplest type of expression with two variables, namely, a linear expression. The expression \(x-4y+8\) is an example of a linear expression with two variables. A linear expression in two variables is formed by multiplying each variable by a number and then adding or subtracting the results.
An expression that can be written as
\(A x+B y+C\)
with \(A\) and \(B\) real numbers, not both zero, is called a linear expression (with two variables), or more specifically, a linear expression in \(x\) and \(y\).
Here is an example of a linear expression with two variables, \(x\) and \(y\).
Evaluate the linear expression \(x-4y+8\) at
a. \(x=-1\) and \(y=5\)
b. \(x=2\) and \(y=0\)
Solution
This expression is in the form \(Ax+By+C\) with \(A=1\), \(B=-4\), and \(C=8\).
We can evaluate this expression for different values of \(x\) and \(y\). For example:
| Values of \(x\) and \(y\) | Evaluating \(x-4y+8\) at \(x\) and \(y\) |
|---|---|
| \(x=-1\) and \(y=5\) | \(\begin{align*} & \; x-4y+8 \\ = &\;(-1-4(5)+8)\\ = &\;-1-20+8\\ = &\;-13\end{align*}\) |
| \(x=2\) and \(y=0\) | \(\begin{align*}&\;x-4y+8\\ = &\;(2-4(0)+8)\\ = &\;2+8\\ = &\;10\end{align*}\) |
Evaluate the linear expression \(3x+2y−15\) at
a. \(x=3\) and \(y=0\)
b. \(x=-5\) and \(y=-1\)
c. \(x=0\) and \(y=2\)
- Answer
-
a. \(-6\)
b. \(-32\)
c. \(−11\)
We can add two linear expressions to get another linear expression. For example,
\(\begin{align*}&\;x-4y+8+(-2x+y-6)\\ =&\;-x-3y+2,\end{align*}\)
using the fact that we can add in any order and 1 \(x\) -2 \(x\)'s is -1 \(x\) (if you have 1 dime and take away 2 dimes, you are down one dime), and -4 \(y\)'s plus 1 \(y\)'s is -3 \(y\)'s (if you have have loaned 4 quarters and then got 1 quarters, you have loaned a total of 3 quarters).
The expression \(x-4y+8+(-2x+y-6)\) is equivalent to \(-x-3y+2\). The expression is of the form \(Ax+By+C\), with \(A=-1, B=-3\), and \(C=2\), so \(x- 4y+8+(-2x+y-6)\) is a linear expression in two variables. We will check this equivalence for a couple of different values for \(x\) and \(y\).
| Values of \(x\) and \(y\) | Evaluating \(x-4y+8+(-2x+y-6)\) at \(x\) and \(y\) | Evaluating \(-x-3y+2\) at \(x\) and \(y\) |
|---|---|---|
| \(x=-1\) and \(y=2\) |
\(\begin{align*} & \;x-4y+8+(-2x+y-6) \\ = &\;(-1)-4(2)+8+(-2(-1)+2-6) \\ = &\;-1-8+8+2+2-6\\ = &\; =-3\end{align*}\) |
\(\begin{align*} & \; -x-3y+2\\ = &\;-(-1)-3(2)+2\\ = &\; 1-6+2\\ = &\;-3 \end{align*}\) |
| \(x=1\) and \(y=3\) |
\(\begin{align*} & \; x-4y+8+(-2x+y-6)\\ = &\;1-4(3)+8+(-2(1)+3-6)\\ = &\;1-12+8-2+3-6\\ = &\;-8\end{align*}\) |
\(\begin{align*} & \; -x-3y+2\\ = &\;-(1)-3(3)+2\\ = &\;-1-9+2\\ = &\;-8 \end{align*}\) |
To subtract a linear expression \(Ax+By+x\) in two variables, we must add the opposite \(-Ax+(-B)y+-C=-Ax-By-C\).
For example,
\(3x-2y-2-(2x-4y+2)=3x-2y-2+(-2)x+4y-2=3x-2x-2y+4y-2-2=x+2y-4.\)
As in the linear expression with one variable, we can multiply a linear expression by a number and still have a linear expression.
For example, \(2(2x-3y+1)\) is \(2(2x)-2(3y)+2(1)\). This is to say that we can 'distribute' the multiplication by 2 'over addition and subtraction', that is, we can multiply 2 by each term. The same would be true if that 2 were replaced by any number!
So,
\(\begin{align*} &\;2(2x-3y+1) \\ = &\;2(2x)-2(3y)+2(1)\\ = &\;4x-6y+2\end{align*}\)
which is of the form \(Ax+By+C\) where \(A=4\), \(B=-6\) and \(C=2\).
Simplify:
a. \(3(x-3y+7)\)
b. \(3x-7y+2-(2x+y-1)\)
c. \(2a-4b+2(5b-2a-1)\)
Solution
a.
| \(\quad 3(x-3y+7)\) | |
|---|---|
|
Distribute. |
\(=3x-(3)3y+3\cdot 7\) |
| Multiply coefficients. | \(=3x-9y+3\) |
b.
| \(\quad 3x-7y+2-(2x+y-1)\) | |
|---|---|
| Distribute. | \( =3x-7y+2-2x-y+1\) |
| Collect like terms. | \(= x-8y+3\) |
c.
| \(\quad 2a-4b+2(5b-2a-1)\) | |
|---|---|
| Distribute. | \(=2a-4b+2(5b)-2(2a)-2(1)\) |
| Simplify. | \(=2a-4b+10b-4a-2\) |
| Collect like terms. | \( =-2a+6b-2\) |
Simplify:
a. \(-3(2x-y-2)\)
b. \(-(3x-7y+2)+(2x+y-1)\)
c. \(3(2a-4b)-2(5b-2a-1)\)
- Answer
-
a. \(-6x+3y+6\)
b. \(-x+8y-3\)
c. \(10a-22b+2\)
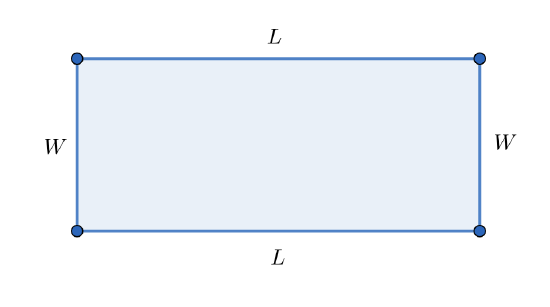
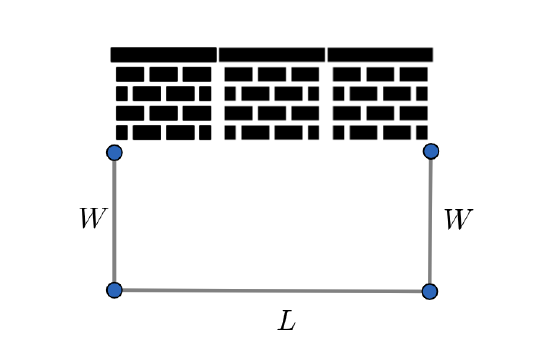
Draw an appropriate picture and express the following quantities in terms of appropriate variables
a. The perimeter of a rectangle of length \(L\) and width \(W\).
b. The amount of fencing needed to enclose an area up against a wall whose length is \(L\) feet and width is \(W\) feet. Suppose that the side consisting of the wall is length \(L\) feet.
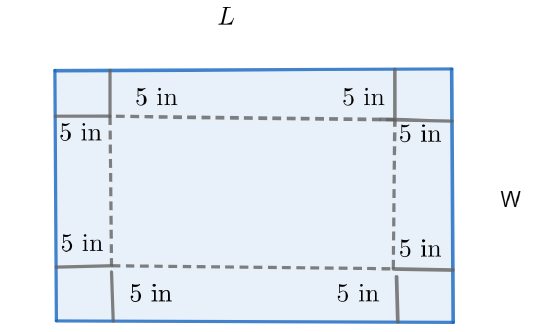
c. If we make a box of height \(5 \textrm{ in}\), with no top, by cutting square corners from a \(L\) in by \(W\) in piece or cardboard and folding them up what are the dimensions of the base of the box? What is the biggest \(L\) can be?
Solution
a. \(L+W+L+W=2L+2W\)
b. \(W+L+W\)
c. Draw a picture (see below). We are interested in the dimensions of the dotted figure. We see that it must be \(L-10\) by \(W-10\); \(L\) must be at least 10 but there is no upper bound to its length.
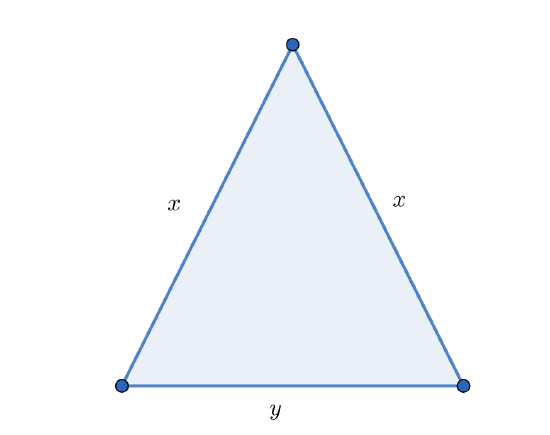
Draw an appropriate picture and express the following quantities in terms of appropriate variables
a. The perimeter of an isosceles triangle with two sides of length \(x\) and one of length \(y\).
b. The amount of fencing needed to enclose an "L" shaped area below.
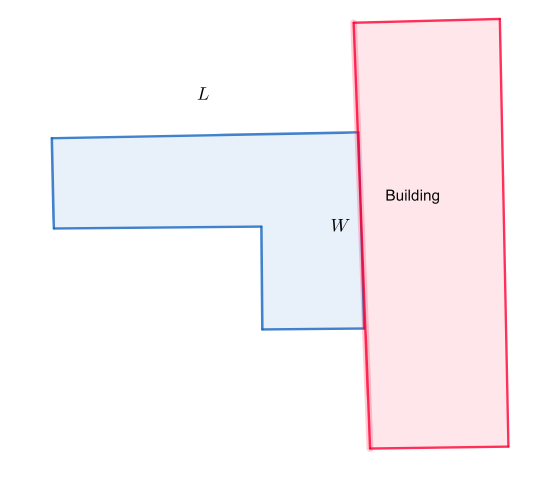
c. If we make a box of height \(x \textrm{ in}\), with no top, by cutting square corners from an \(L\) in by \(10\) in piece or cardboard and folding them up what are the dimensions of the base of the box? What is the biggest \(x\) can be if \(L=12\textrm{ in}\)?
- Answer
-
a. \(2x+y\)
b. \(L+W+L\)
c. \(L-2x\) by \(10-2x\); if \(L=12\), the box is \(12-2x\) by \(10-2x\) so \(x\) must be less than \(5\textrm{ in}\).
Linear Expressions in more than Two Variables
This idea can be extended in a clear way to more than two variables leading to expressions that look like \(2x-3y+3z-6w+2\). We won't discuss this any further because the concepts are similar to the above.
Additional Notes
Note that the linear expression of the standard forms given in the definitions are easy to evaluate. The process of writing an expression that is 'harder' to evaluate as an equivalent expression that is 'easier' to evaluate is called simplification. This concept of simplification is sometimes depends on the context or application involved.
Also, note that we have named our variables here \(x\) and \(y\) but it doesn't matter what you name them. You could use 'earth' and 'mars' or anything else that may be convenient. Usually the names are short (one letter if possible) because it saves a lot of writing.
Note that \(A, B,\) and \(C\) don't have to be integers. Important algebraic concepts that can be learned here in the process of simplification of linear expressions are
- What it means to collect like terms
- The 'opposite' of an expression is the one obtained by negating each term
- To subtract an expression, we add its opposite
- We can distribute multiplication over addition and subtraction
Key concepts
- Variable
- Linear expressions in one and two variables
- Collecting like terms
- Opposite of a linear expression
- Adding and subtracting linear expressions
- Distribution of multiplication over addition and subtraction
- Simplification