1.2.3: Multiplying Polynomials
- Page ID
- 94672
By the end of this section, you will be able to:
- Multiply monomials
- Multiply a polynomial by a monomial
- Multiply a binomial by a binomial
- Multiply a polynomial by a polynomial
- Multiply special products
Before you get started, take this readiness quiz.
1. Distribute: \(2(x+3)\).
2. Simplify:
a. \(9^2\)
b. \((−9)^2\)
c. \(−9^2\)
3. Evaluate \(2x^2−5x+3\) for \(x=−2\).
Multiplying Expressions Using a Property for Exponents
Remember that a positive integer exponent indicates repeated multiplication of the same quantity. For example, in the expression \(a^m\), the positive integer exponent \(m\) tells us how many times we use the base \(a\) as a factor.
\[a^{m}= \underbrace{a \cdot a \cdot a \cdot \ldots \cdot a}_{\text{m factors}} \nonumber\]
For example,
\[(-9)^{5}= \underbrace{ (-9)\cdot (-9)\cdot (-9)\cdot (-9) \cdot (-9)}_{\text{5 factors}} \nonumber\]
Let’s review the vocabulary for expressions with exponents.
\(a^m = \underbrace{a\cdot a\cdot a \cdots a}_{m \text{ factors }}\)
This is read \(a\) to the \(m^{th}\) power.
In the expression \(a^m\) with positive integer \(m\) and \(a\not=0\), the exponent \(m\) tells us how many times we use the base \(a\) as a factor.
When we combine like terms by adding and subtracting, we need to have the same base with the same exponent. But when we multiply and divide, the exponents may be different, and sometimes the bases may be different, too.
First, we will look at an example that leads to the Product Property for Positive Integer Exponents.
|
\(\quad x^{2} x^{3}\) |
|
|---|---|
| What does this mean? |
\(=\underbrace{x \cdot x}_{2 \text{ factors}\space} \cdot \underbrace{ x\cdot x\cdot x}_{3 \text{ factors}}\) \(=\underbrace{x\cdot x\cdot x\cdot x\cdot x}_{5 \text{ factors}}\) |
| \(= x^{5}\) |
The base stayed the same and we added the exponents.
If \(a\) is a real number and \(m\) and \(n\) are positive integers, then
\[a^ma^n=a^{m+n}. \nonumber\]
To multiply with like bases, add the exponents.
Simplify each expression:
a. \(y^5y^6\)
b. \(2^4\cdot 2^{3\cdot 4}\)
c. \(2a^7\cdot 3a\)
d. \(d^4d^5d^2\)
Solution
a.
| \(\quad y^5y^6\) | |
|---|---|
| Use the Product Property, \(a^ma^n=a^{m+n}\). | \(=y^{5+6}\) |
| Simplify. | \(=y^{11}\) |
b.
| \(\quad\; 2^4\cdot 2^{3\cdot 4}\) | |
|---|---|
| Use the Product Property, \(a^ma^n=a^{m+n}\). | \(=2^{4+3\cdot 4}\) |
| Simplify. |
\(=2^{4\cdot 4}\) \(=2^{16}\) |
c.
| \(\quad\; 2a^7\cdot 3a\) | |
|---|---|
| Rewrite, \(a=a^1\). | \(= 2a^7\cdot 3a^1\) |
| Use the Commutative Property and use the Product Property, \(a^ma^n=a^{m+n}\). |
\(=2\cdot 3a^{7+1}\) |
| Simplify. | \(=6a^8\) |
d.
| \(\quad d^4d^5d^2\) | |
|---|---|
| Add the exponents, since the bases are the same. | \(= d^{4+5+2}\) |
| Simplify. | \(=d^{11}\) |
Simplify each expression:
a. \(b^9b^8\)
b. \(4^{2\cdot 3}\cdot 4^3\)
c. \(3p^5\cdot 4p\)
d. \(x^6x^4x^8\)
- Answer
-
a. \(b^{17}\)
b. \(4^9\)
c. \(12p^6\)
d. \(x^{18}\)
Simplify each expression:
a. \(x^{12}x^4\)
b. \(10\cdot 10^5\)
c. \(2z\cdot 6z^7\)
d. \(b^5b^9b^5\)
- Answer
-
a. \(x^{16}\)
b. \(10^{6}\)
c. \(12z^8\)
d. \(b^{19}\)
Multiplying Monomials
We are ready to perform operations on polynomials. Since monomials are algebraic expressions, we can use the properties of exponents to multiply monomials.
Multiply:
a. \((3x^2)(−4x^3)\)
b. \(\left(\dfrac{5}{6}x^3y\right)(12xy^2)\)
Solution
a.
| \(\quad (3x^2)(−4x^3)\) | |
|---|---|
| Use the Commutative Property and use the Product Property, \(a^ma^n=a^{m+n}\). |
\(=3(-4)x^2x^3\) |
| Simplify. | \(=−12x^5\) |
b.
| \(\quad \left(\dfrac{5}{6}x^3y\right)(12xy^2)\) | |
|---|---|
| Use the Commutative Property and use the Product Property, \(a^ma^n=a^{m+n}\). |
\(=\dfrac{5}{6}\cdot 12x^3x\cdot yy^2\) |
| Simplify. | \(=10x^4y^3\) |
Multiply:
a. \((5y^7)(−7y^4)\)
b. \((25a^4b^3)(15ab^3)\)
- Answer
-
a. \(−35y^{11}\)
b. \(6a^5b^6\)
Multiply:
a. \((−6b^4)(−9b^5)\)
b. \((23r^5s)(12r^6s^7).\)
- Answer
-
a. \(54b^9\)
b. \(8r^{11}s^8\)
Multiplying a Polynomial by a Monomial
Multiplying a polynomial by a monomial is really just applying the Distributive Property of multiplication over addition and subtraction.
Multiply:
a. \(−2y(4y^2+3y−5)\)
b. \(3x^3y(x^2−8xy+y^2)\)
Solution
a.
| \(\quad −2y(4y^2+3y−5)\) | |
|---|---|
| Distribute. | \(= −2y\cdot 4y^2+(-2y)3y+(-2y)(−5))\) |
| Simplify. | \(=-8y^3-6y^2+10y\) |
b.
| \(\quad 3x^3y(x^2−8xy+y^2)\) | |
|---|---|
| Distribute. | \(=3x^3yx^2−3x^3y\cdot 8xy+3x^3yy^2)\) |
| Simplify. | \(=3x^5y-24x^4y^2+3x^3y^3\) |
Multiply:
a. \(-3y(5y^2+8y^{−7})\)
b. \(4x^2y^2(3x^2−5xy+3y^2)\)
- Answer
-
a. \(−15y^3−24y^2+21y\)
b. \(12x^4y^2−20x^3y^3+12x^2y^4\)
Multiply:
a. \(4x^2(2x^2−3x+5)\)
b. \(−6a^3b(3a^2−2ab+6b^2)\)
- Answer
-
a. \(−15y^3−24y^2+21y\)
b. \(−18a^5b+12a^4b^2−36a^3b^3\)
Multiplying a Binomial by a Binomial
The multiplication of a binomial by a binomial can be performed by multiplying the each term of one binomial by the other binomial. This is seen by applying the Distributive Property twice.
\(\begin{align*} (a+b)(c+d) &= a(c+d) + b(c+d)\\ &=ac+ad+bc+bd\end{align*}\)
Multiply:
a. \((y+5)(y+8)\)
b. \((4y+3)(2y−5)\)
Solution
a.
| \(\quad(y+5)(y+8)\) | |
|---|---|
| Distribute \(y+8\). | \(=y(y+8)+5(y+8)\) |
| Distribute again. | \(=y^2+8y+5y+40\) |
| Combine like terms | \(=y^2+13y + 40\) |
Note that you could have distributed the \(y+5\) instead on the first step and proceeded from there.
b.
| \(\quad(4y+3)(2y−5)\) | |
|---|---|
| Distribute \(2y-5\). | \(=4y(2y-5)+3(2y-5)\) |
| Distribute again. | \(=8y^2-20y+6y-15\) |
| Combine like terms. | \(=8y^2-14y-15\) |
Multiply:
a. \((x+8)(x+9)\)
b. \((3c+4)(5c−2)\)
- Answer
-
a. \(x^2+17x+72\)
b. \(15c^2+14c−8\)
Multiply:
a. \((5x+9)(4x+3)\)
b. \((5y+2)(6y−3)\)
- Answer
-
a. \(20x^2+51x+27\)
b. \(30y^2−3y−6\)
If you multiply binomials often enough you may notice a pattern. Notice that the first term in the result is the product of the first terms in each binomial. The second and third terms are the product of multiplying the two outer terms and then the two inner terms. And the last term results from multiplying the two last terms,
We abbreviate “First, Outer, Inner, Last” as FOIL. The letters stand for ‘First, Outer, Inner, Last’. We use this as another method of multiplying binomials. The word FOIL is easy to remember and ensures we find all four products.
Let’s multiply \((x+3)(x+7)\) using the Distributive Property ( or FOIL).
| Distribute Property | FOIL |
|---|---|
| \(\quad (x+3)(x+7)\) | \(\quad (x+3)(x+7)\) |
| \(= x(x+7)+3(x+7)\) | \(=\underbrace{x^2}_{\text{F}}+\underbrace{7x}_{\text{O}}+\underbrace{3x}_{\text{I}}+\underbrace{21}_{\text{L}}\) |
| \(=x^2+7x+3x+21\) | \(=x^2+10x+21\) |
| \(=x^2+10x+21\) |
The following chart explains in details how to multiply binomials using FOIL. Note that FOIL does not work with other polynomials (why?)!
| \(\quad (a+b)(c+d)\) | |
|---|---|
| Identify first, outer, inner and last terms. |
\(= (\underbrace{\overbrace{a}^{\text{outer}}}_{\text{first}}+\underbrace{\overbrace{b}^{\text{inner}}}_{\text{last}})(\underbrace{\overbrace{c}^{\text{inner}}}_{\text{first}}+\underbrace{\overbrace{d}^{\text{outer}}}_{\text{last}})\) |
| Multiply the first terms. (F) | \(=\underbrace{ac}_{\text{F}} + \underbrace{\_\_}_{\text{O}} + \underbrace{\_\_}_{\text{I}}+ \underbrace{\_\_}_{\text{L}}\) |
| Multiply the outer terms. (O) | \(=\underbrace{ac}_{\text{F}} + \underbrace{ad}_{\text{O}} + \underbrace{\_\_}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the inner terms. (I) |
\(=\underbrace{ac}_{\text{F}} + \underbrace{ad}_{\text{O}} +\underbrace{bc}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the last terms.(L) | \(=\underbrace{ac}_{\text{F}} + \underbrace{ad}_{\text{O}} + \underbrace{bc}_{\text{I}} +\underbrace{bd}_{\text{L}}\) |
| Combine like terms, when possible. | \(=ac+ad+bc+bc\) |
When you multiply using FOIL, drawing the lines will help your brain focus on the pattern and make it easier to apply.
Now we will do an example where we use the FOIL pattern to multiply two binomials.
Multiply:
a. \((y−7)(y+4)\)
b. \((4x+3)(2x−5)\)
Solution
a.
| \(\quad (y-7)(y+4)\) | |
|---|---|
| Identify first, outer, inner and last terms. |
\(= (\underbrace{\overbrace{y}^{\text{outer}}}_{\text{first}}+\underbrace{\overbrace{(-7)}^{\text{inner}}}_{\text{last}})(\underbrace{\overbrace{y}^{\text{inner}}}_{\text{first}}+\underbrace{\overbrace{4}^{\text{outer}}}_{\text{last}})\) |
| Multiply the first terms. (F) | \(=\underbrace{y^2}_{\text{F}} + \underbrace{\_\_}_{\text{O}} + \underbrace{\_\_}_{\text{I}}+ \underbrace{\_\_}_{\text{L}}\) |
| Multiply the outer terms. (O) | \(=\underbrace{y^2}_{\text{F}} + \underbrace{4y}_{\text{O}} + \underbrace{\_\_}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the inner terms. (I) |
\(=\underbrace{y^2}_{\text{F}} + \underbrace{4y}_{\text{O}} +\underbrace{(-7y)}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the last terms.(L) | \(=\underbrace{y^2}_{\text{F}} + \underbrace{4y}_{\text{O}} + \underbrace{(-7y)}_{\text{I}} +\underbrace{(-28)}_{\text{L}}\) |
| Combine like terms, when possible. |
\(=y^2+4y-7y-28\) \(=y^2-3y-28\) |
b.
| \(\quad(4x+3)(2x−5)\) | |
|---|---|
| Identify first, outer, inner and last terms. |
\(= (\underbrace{\overbrace{4x}^{\text{outer}}}_{\text{first}}+\underbrace{\overbrace{3}^{\text{inner}}}_{\text{last}})(\underbrace{\overbrace{2x}^{\text{inner}}}_{\text{first}}+\underbrace{\overbrace{(-5)}^{\text{outer}}}_{\text{last}})\) |
| Multiply the first terms. (F) | \(=\underbrace{8x^2}_{\text{F}} + \underbrace{\_\_}_{\text{O}} + \underbrace{\_\_}_{\text{I}}+ \underbrace{\_\_}_{\text{L}}\) |
| Multiply the outer terms. (O) | \(=\underbrace{8x^2}_{\text{F}} + \underbrace{(-20x)}_{\text{O}} + \underbrace{\_\_}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the inner terms. (I) |
\(=\underbrace{8x^2}_{\text{F}} + \underbrace{(-20x)}_{\text{O}} +\underbrace{6x}_{\text{I}} +\underbrace{\_\_}_{\text{L}}\) |
| Multiply the last terms.(L) | \(=\underbrace{8x^2}_{\text{F}} + \underbrace{(-20x)}_{\text{O}} + \underbrace{6x}_{\text{I}} +\underbrace{(-15)}_{\text{L}}\) |
| Combine like terms, when possible. |
\(=8x^2+(-20x)+6x+(-15)\) \(=8x^2-14x-15\)
|
Multiply:
a. \((x−7)(x+5)\)
b. \((3x+7)(5x−2)\)
- Answer
-
a. \(x^2−2x−35\)
b. \(15x^2+29x−14\)
Multiply:
a. \((b−3)(b+6)\)
b. \((4y+5)(4y−10)\)
- Answer
-
a. \(b^2+3b−18\)
b. \(16y^2−20y−50\)
The final products in the last example were trinomials because we could combine the two middle terms. This is not always the case.
Multiply:
a. \((n^2+4)(n−1)\)
b. \((3pq+5)(6pq−11)\)
Solution
a.
| \(\quad(n^2+4)(n−1)\) | |
|---|---|
| Identify first, outer, inner and last terms. |
\(= (\underbrace{\overbrace{n^2}^{\text{outer}}}_{\text{first}}+\underbrace{\overbrace{4}^{\text{inner}}}_{\text{last}})(\underbrace{\overbrace{n}^{\text{inner}}}_{\text{first}}+\underbrace{\overbrace{(-1)}^{\text{outer}}}_{\text{last}})\) |
| Multiply the first terms. (F) | \(=\underbrace{n^3}_{\text{F}} + \underbrace{\_\_\_}_{\text{O}} + \underbrace{\_\_\_}_{\text{I}}+ \underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the outer terms. (O) | \(=\underbrace{n^3}_{\text{F}} + \underbrace{(-n^2)}_{\text{O}} + \underbrace{\_\_\_}_{\text{I}} +\underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the inner terms. (I) |
\(=\underbrace{n^3}_{\text{F}} + \underbrace{(-n^2)}_{\text{O}} +\underbrace{4n}_{\text{I}} +\underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the last terms.(L) | \(=\underbrace{n^3}_{\text{F}} + \underbrace{(-n^2)}_{\text{O}} + \underbrace{4n}_{\text{I}} +\underbrace{(-4)}_{\text{L}}\) |
| Combine like terms, when possible. |
\(=n^3+(-n^2)+4n+(-4)\) \(=n^3-n^2+4n-4\)
|
b.
| \(\quad(3pq+5)(6pq−11)\) | |
|---|---|
| Identify first, outer, inner and last terms. |
\(= (\underbrace{\overbrace{3pq}^{\text{outer}}}_{\text{first}}+\underbrace{\overbrace{5}^{\text{inner}}}_{\text{last}})(\underbrace{\overbrace{6pq}^{\text{inner}}}_{\text{first}}+\underbrace{\overbrace{(-11)}^{\text{outer}}}_{\text{last}})\) |
| Multiply the first terms. (F) | \(=\underbrace{15p^2q^2}_{\text{F}} + \underbrace{\_\_\_}_{\text{O}} + \underbrace{\_\_\_}_{\text{I}}+ \underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the outer terms. (O) | \(=\underbrace{15p^2q^2}_{\text{F}} + \underbrace{(-33pq)}_{\text{O}} + \underbrace{\_\_\_}_{\text{I}} +\underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the inner terms. (I) |
\(=\underbrace{15p^2q^2}_{\text{F}} + \underbrace{(-33pq)}_{\text{O}} +\underbrace{30pq}_{\text{I}} +\underbrace{\_\_\_}_{\text{L}}\) |
| Multiply the last terms.(L) | \(=\underbrace{15p^2q^2}_{\text{F}} + \underbrace{(-33pq)}_{\text{O}} + \underbrace{30pq}_{\text{I}} +\underbrace{(-55)}_{\text{L}}\) |
| Combine like terms, when possible. |
\(=15p^2q^2+(-33pq)+30pq+(-55)\) \(=15p^2q^2-3pq+4n-55\)
|
Multiply:
a. \((x^2+6)(x−8)\)
b. \((2ab+5)(4ab−4)\)
- Answer
-
a. \(x^3−8x^2+6x−48\)
b. \(8a^2b^2+12ab−20\)
Multiply:
a. \((y^2+7)(y−9)\)
b. \((2xy+3)(4xy−5)\)
- Answer
-
a. \(y^3−9y^2+7y−63\)
b. \(8x^2y^2+2xy−15\)
The FOIL method is just one way to keep track of the four terms that appear in the product of two binomials, and it only works for binomials. Another way for obtaining the four term is using the Vertical format. It is very much like the procedure you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.
\[\begin{align*}&32\\ \times &35\\ \hline\\ &160\\+&96*\\ \hline \\ &1120\end{align*}\]
Now we’ll apply this same procedure to multiply two binomials.
Multiply \((3y−1)(2y−6)\) using the Vertical format.
Solution
It does not matter which binomial goes on the top.
| \(\quad(3y−1)(2y−6)\) | |
|
Multiply \(3y−1\) by \(−6\). Multiply \(3y−1\) by \(2y\). |
\(-18y+6\) \(+6y^2-2y\) |
| Add like terms. | \(=6y^2-20y+6\) |
Multiply \((5m−7)(3m−6)\) using the Vertical format.
- Answer
-
\(15m^2−51m+42\)
Multiply \((6b−5)(7b−3)\) using the Vertical format.
- Answer
-
\(42b^2−53b+15\)
Multiplying a Polynomial by a Polynomial
We have multiplied monomials by monomials, monomials by polynomials, and binomials by binomials. Now we’re ready to multiply a polynomial by a polynomial. Remember, FOIL will not work in this case, but we use the Distributive Property. There are various ways to keep track of the terms. The first is to just note one way to see the why we can distribute!
Consider finding the area of the marked figure below:
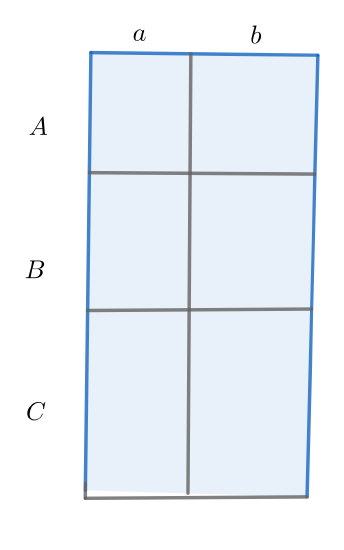
One way to calculate the area is to find the width (\(a+b\)) and the length (\(A+B+C\)) and then multiply to get:
\((a+b)(A+B+C)\)
The other way is to find the area of each little rectangle (indicated here inside the corresponding rectangle)
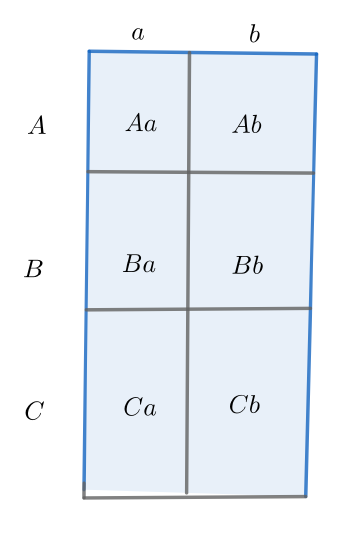
and then add the results (in whichever order we like) to get, for example, that the area is also equal to
\(Aa+Ab+Ba+Bb+Ca+Cb\)
Notice that we have in this example, six terms, each of which is the result of the product of a length from the first grouping times a length of the second grouping.
Since the area is the same no matter how we compute it, we have, for example,
\((a+b)(A+B+C)=Aa+Ab+Ba+Bb+Ca+Cb.\)
The picture only is valid for positive values since only such values represent length, but the equation is true for all values (and a picture can be drawn to specifically indicate negative quantities as length subtraction). The picture here then can generally be used for bookkeeping purposes no matter if the values of \(a, b, A, B,\) and \(C\) are all positive.
Multiply \((b+3)(2b^2−5b+8)\).
Solution
We present three solutions.
First, we create the rectangle and labeling above in this case for the purpose of book-keeping (and ignore the fact that negative values can not be lengths):
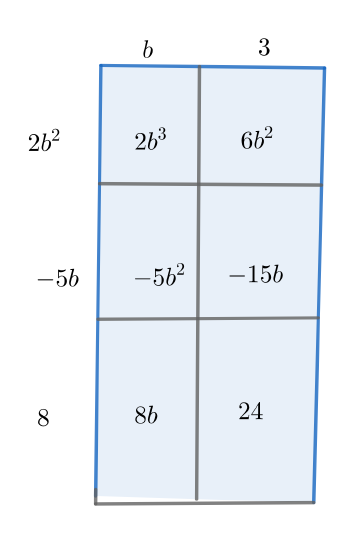
To find \(b+3)(2b^2−5b+8)=2b^3+6b^2-5b^2-15b+8b+24=2b^3+b^2-7b+24\)
(the last equality we see by collecting like terms).
The second way is by using the Distributive Property of multiplication of monomials over addition/subtraction.
| \(\quad (b+3)(2b^2−5b+8)\) | |
|---|---|
| Distribute. | \(=b(2b^2−5b+8) +3(2b^2−5b+8)\) |
| Distribute. |
\(=2b^3-5b^2+8b+6b^2-15b+24\) |
| Combine like terms. |
\(=2b^3+b^2-7b+24\) |
The third way is using the vertical format. It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.
| \(\quad (b+3)(2b^2−5b+8)\) | ||
|---|---|---|
| Multiply \((2b^2−5b+8)\) by 3. Multiply \((2b^2−5b+8)\) by \(b\). |
\(=6b^2-15b+24\) \(+2b^3-5b^2+8b\) |
|
| Add like terms. | \(=2b^3+b^2-7b+24\) | |
Multiply \((y−3)(y^2−5y+2)\).
- Answer
-
a. \(y^3−8y2+17y−6\)
b. \(y^3−8y2+17y−6\)
Multiply \((x+4)(2x^2−3x+5)\).
- Answer
-
a. \(2x^3+5x^2−7x+20\)
b. \(y^3−8y^2+17y−6\)
Multiplying Special Products
Sometimes identifying patterns will make computations 'easier'. A good example of this is squaring binomials. While you can always get the product by writing the binomial twice and multiplying them, there is less work to do if you learn to use a pattern. Let’s start by looking at three examples and look for a pattern.
Look at these results. Do you see any patterns?
\[(x-5)^2=x^2-10x+25, \quad (2y+3)^2=4y^2+12y+9, \quad (5z-2t)^2=25z^2-20zt+4t^2\nonumbe\]
What about the number of terms? In each example we squared a binomial and the result was a trinomial.
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
Now look at the first term in each result. Where did it come from?
The first term is the product of the first terms of each binomial. Since the binomials are identical, it is just the square of the first term!
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
To get the first term of the product, square the first term.
Where did the last term come from? Look at the examples and find the pattern.
The last term is the product of the last terms, which is the square of the last term.
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
To get the last term of the product, square the last term.
Finally, look at the middle term. Notice it came from adding the “outer” and the “inner” terms—which are both the same! So the middle term is double the product of the two terms of the binomial.
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
To get the middle term of the product, multiply the terms and double their product.
Putting it all together:
If \(a\) and \(b\) are real numbers,
|
\(\underbrace{(a+b)^2}_{\text{(binomial)}^2}=\underbrace{a^2}_{(\text{first term})^2}+\underbrace{2ab}_{2(\text{product of terms})}+\underbrace{b^2}_{\text{(last term)}^2},\) \(\underbrace{(a-b)^2}_{\text{(binomial)}^2}=\underbrace{a^2}_{(\text{first term})^2}-\underbrace{2ab}_{2(\text{product of terms})}+\underbrace{b^2}_{\text{(last term)}^2}.\) |
|---|
To square a binomial, square the first term, square the last term, double their product.
Multiply:
a. \((x+5)^2\)
b. \((2x−3y)^2\)
Solution
a.
| \(\quad(x+5)^2\) | |
|---|---|
| Identify \(a\) and \(b\). | \(=(\underbrace{x}_{a}+\underbrace{5}_{b})^2\) \(\quad\quad a=x,\;b=5\) |
| Square the first term, \(a\). | \(=\underbrace{x^2}_{a^2}+\underbrace{\_\_\_}_{2ab}+\underbrace{\_\_\_}_{b^2}\) |
| Double the product of \(a\) and \(b\). | \(=\underbrace{x^2}_{a^2}+\underbrace{2\cdot (x)\cdot (5)}_{2ab}+\underbrace{\_\_\_}_{b^2}\) |
| Square the last term, \(b\). | \(=\underbrace{x^2}_{a^2}+\underbrace{2\cdot (x)\cdot (5)}_{2ab}+\underbrace{5^2}_{b^2}\) |
| Simplify. | \(=x^2+10x+25\) |
b.
| \(\quad(2x-3y)^2\) | |
|---|---|
| Identify \(a\) and \(b\). | \(=(\underbrace{2x}_{a}-\underbrace{3y}_{b})^2\)\(\quad\quad a=2x,\; b=3y\) |
| Square the first term, \(a\). | \(=\underbrace{(2x)^2}_{a^2}-\underbrace{\_\_\_}_{2ab}+\underbrace{\_\_\_}_{b^2}\) |
| Double the product of \(a\) and \(b\). | \(=\underbrace{(2x)^2}_{a^2}-\underbrace{2\cdot (3x)\cdot (3y)}_{2ab}+\underbrace{\_\_\_}_{b^2}\) |
| Square the last term, \(b\). | \(=\underbrace{x^2}_{a^2}-\underbrace{2\cdot (3x)\cdot (3y)}_{2ab}+\underbrace{(3y)^2}_{b^2}\) |
| Simplify. | \(=4x^2-12xy+9y^2\) |
Multiply:
a. \((x+9)^2\)
b. \((2c−d)^2\)
- Answer
-
a. \(x^2+18x+81\)
b. \(4c^2−4cd+d^2\)
Multiply:
a. \((y+11)^2\)
b. \((4x−5y)^2\)
- Answer
-
a. \(y^2+22y+121\)
b. \(16x^2−40xy+25y^2\)
We just saw a pattern for squaring binomials that we can use to make multiplying some binomials easier. Similarly, there is a pattern for another product of binomials. But before we get to it, we need to introduce some vocabulary.
A pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference is called a conjugate pair and is of the form \((a−b)\), \((a+b)\).
A conjugate pair is two binomials of the form
\[(a−b), (a+b). \nonumber\]
The pair of binomials each have the same first term and the same last term, but one binomial is a sum and the other is a difference.
There is a nice pattern for finding the product of conjugates. You could, of course, simply FOIL to get the product, but using the pattern makes your work easier. Let’s look for the pattern by using FOIL to multiply some conjugate pairs.
\[(x-4)(x+4)=x^2+4x-4x-16=x^2-16\nonumber\]
\[(2x+3)(2x-3)=4x^2-6x+6x-9=4x^2-9\nonumber\]
\[(3z-2t)(3z+2t)=9z^2+6zt-6tz-4t^2=9z^2-4t^2\nonumber\]
What do you observe about the products?
The product of the two binomials is also a binomial! Most of the products resulting from FOIL have been trinomials.
Each first term is the product of the first terms of the binomials, and since they are identical it is the square of the first term.
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
To get the first term, square the first term.
The last term came from multiplying the last terms, the square of the last term.
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
To get the last term, square the last term.
Why is there no middle term? Notice the two middle terms you get from FOIL combine to 0 in every case, the result of one addition and one subtraction.
The product of conjugates is always of the form \(a^2−b^2\). This is called a difference of squares.
This leads to the pattern:
For any \(a\) and \(b\),
\[(a+b)(a-b)=a^2-b^2\nonumber\]The product is called a difference of squares.
To multiply conjugates, square the first term, square the last term, write it as a difference of squares.
Multiply using the product of conjugates pattern:
a. \((2x+5)(2x−5)\)
b. \((5m−9n)(5m+9n)\)
Solution
a.
| \(\quad (2x+5)(2x−5)\) | |
|---|---|
|
Are the binomials conjugates? Identify \(a\) and \(b\) |
The binomials \(2x+5\) and \(2x-5\) are conjugates. \(\quad\quad a=2x,\;b=5\) |
| It is the product of conjugates. | \(=(\underbrace{2x+5}_{a+b})(\underbrace{2x-5}_{a-b})\) |
| Square the first term, \(a\). | \(=\underbrace{(2x)^2}_{a^2}-\underbrace{\_\_\_}_{b^2}\) |
| Square the last term, \(b\). | \(=\underbrace{(2x)^2}_{a^2}-\underbrace{(5)^2}_{b^2}\) |
|
Simplify. The product is a difference of squares. |
\(=4x^2-25\) |
b.
| \(\quad (5m-9n)(5m+9n)\) | |
|---|---|
|
Are the binomials conjugates? Identify \(a\) and \(b\). |
The binomials \(5m-9n\) and \(5m+9n\) are conjugates. \(\quad\quad a = 5m, \; b=9n\) |
| It is the product of conjugates. | \(=(\underbrace{5m-9n}_{a-b})(\underbrace{5m+9n}_{a+b})\) |
| Square the first term, \(a\). | \(=\underbrace{(5m)^2}_{a^2}-\underbrace{\_\_\_}_{b^2}\) |
| Square the last term, \(b\). | \(=\underbrace{(5m)^2}_{a^2}-\underbrace{(9n)^2}_{b^2}\) |
|
Simplify. The product is a difference of squares. |
\(=25m^2-81n^2\) |
Multiply:
a. \((6x+5)(6x−5)\)
b. \((4p−7q)(4p+7q)\)
- Answer
-
a. \(36x^2−25\)
b. \(16p^2−49q^2\)
Multiply:
a. \((2x+7)(2x−7)\)
b. \((3x−y)(3x+y)\).
- Answer
-
a. \(4x^2−49\)
b. \(9x^2−y^2\)
We just developed special product patterns for Binomial Squares and for the Product of Conjugates. The products look similar, so it is important to recognize when it is appropriate to use each of these patterns and to notice how they differ. Look at the two patterns together and note their similarities and differences.
| Binomial Squares | Product of Conjugates |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • Squaring a binomial | • Multiplying conjugates |
| • Product is a trinomial | • Product is a binomial. |
| • Inner and outer terms with FOIL are the same. | • Inner and outer terms with FOIL are opposites. |
| • Middle term is double the product of the terms | • There is no middle term. |
Choose the appropriate pattern and use it to find the product:
a. \((2x−3)(2x+3)\)
b. \((5x−8)^2\)
c. \((6m+7)^2\)
d. \((5x−6)(6x+5)\)
Solution
a. \((2x−3)(2x+3)\)
These are conjugates. They have the same first numbers, and the same last numbers, and one binomial is a sum and the other is a difference. It fits the Product of Conjugates pattern.
| \(\quad (\underbrace{2x-3}_{a-b})(\underbrace{2x+3}_{a+b})\quad\quad a=2x,\;b=3\) | |
| Use the pattern: \((a-b)(a+b)=a^2-b^2\). | \(=\underbrace{(2x)^2}_{a^2}- \underbrace{(3)^2}_{b^2}\) |
| Simplify. | \(=4x^2-9\) |
b. \((8x−5)^2\)
We are asked to square a binomial. It fits the binomial squares pattern.
| \(\quad (\underbrace{8x-5}_{a-b})^2\quad\quad a=8x,\;b=5\) | |
| Use the pattern: \((a-b)^2=a^2-2ab+b^2\). | \(=\underbrace{(8x)^2}_{a^2} -\underbrace{2\cdot (8x)\cdot (5)}_{2ab} + \underbrace{(5)^2}_{b^2}\) |
| Simplify. | \(=64x^2+80x+25\) |
c. \((6m+7)^2\)
Again, we will square a binomial so we use the binomial squares pattern.
| \(\quad (\underbrace{6m+7}_{a+b})^2\quad\quad a=6m,\;b=7\) | |
| Use the pattern: \((a+b)^2=a^2+2ab+b^2\). | \(=\underbrace{(6m)^2}_{a^2} +\underbrace{2\cdot (6m)\cdot (7)}_{2ab} + \underbrace{(7)^2}_{b^2}\) |
| Simplify. | \(=36m^2+84m+49\) |
d. \((5x−6)(6x+5)\)
This product does not fit the patterns, so we will use FOIL.
| \(\quad (5x-6)(6x+5)\) | |
| Use FOIL. | \(=30x^2+25x−36x−30\) |
| Simplify. | \(=30x^2−11x−30\) |
Choose the appropriate pattern and use it to find the product:
a. \((9b−2)(2b+9)\)
b. \((9p−4)^2\)
c. \((7y+1)^2\)
d. \((4r−3)(4r+3)\)
- Answer
-
a. FOIL; \(18b^2+77b−18\)
b. Binomial Squares; \(81p^2−72p+16\)
c. Binomial Squares; \(49y^2+14y+1\)
d. Product of Conjugates; \(16r^2−9\)
Choose the appropriate pattern and use it to find the product:
a. \((6x+7)^2\)
b. \((3x−4)(3x+4)\)
c. \((2x−5)(5x−2)\)
d. \((6n−1)^2\)
- Answer
-
a. Binomial Squares; \(36x^2+84x+49\)
b. Product of Conjugates; \(9x^2−16\)
c. FOIL; \(10x^2−29x+10\)
d. Binomial Squares; \(36n^2−12n+1\)
- Explain how the 'FOIL' method is the same as a sequence of two distributions.
- If you multiply two binomials, is the result a binomial? Give an example.
- How many terms does a trinomial times a monomial have?
- Is it possible that the product of a binomial and a trinomial has 7 terms? Explain and give an example.
- What is the minimal amount of work you must do to determine the degree and the leading coefficient of \((5x^3+x^2-2x+1)(-2x^2-7x+2)\)? Explain and give another example of this process.
- Show using a picture that represents a possible situation that \((5-2)(6+2-3)=30+10-15-12-4+6\).
- Which method do you prefer to use when multiplying two binomials: the rectangle, the distributive property for monomials (twice), or the FOIL method? Why? Which method do you prefer to use when multiplying a polynomial by a polynomial: the rectangle, the distributive property for monomials (twice), or the Vertical Method? Why?
- Multiply the following:
\((x+2)(x−2)\)
\((y+7)(y−7)\)
\((w+5)(w−5)\)
Explain the pattern that you see in your answers. Does that pattern persist for \((y+7)(y+7)\)? Give an example.
- Multiply \(3x^3(2x-3)(3x+1)\).
- Multiply \(3x(3x^3y)(2x^3y^4)\).
Key Concepts
- How to use the FOIL method to multiply two binomials.
\[(a+b)(c+d)=ac+ad+bc+bd\] - Multiplying Two Binomials: To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Multiplying a Polynomial by a Polynomial: To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical setup
- Binomial Squares Pattern
If a and b are real numbers, \((a+b)^2=a^2+2ab+b^2\) - Product of Conjugates Pattern
If a, b are real numbers
\[(a+b)(a-b)=a^2-b^2\]
The product is called a difference of squares.
To multiply conjugates, square the first term, square the last term, write it as a difference of squares. - Comparing the Special Product Patterns
Binomial Squares Product of Conjugates \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • Squaring a binomial • Multiplying conjugates • Product is a trinomial • Product is a binomial. • Inner and outer terms with FOIL are the same. • Inner and outer terms with FOIL are opposites. • Middle term is double the product of the terms • There is no middle term.