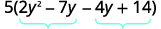1.2.7: Factoring Trinomials
- Page ID
- 93968
By the end of this section, you will be able to:
- Factor trinomials of the form \(x^2+bx+c\)
- Factor trinomials of the form \(ax^2+bx+c\) using trial and error
- Factor trinomials of the form \(ax^2+bx+c\) using the ‘\(ac\)’ method
- Factor using substitution
Before you get started, take this readiness quiz.
1. Find all the factors of \(72\).
2. Find the product \((3y+4)(2y+5)\).
3. Simplify \(−9(6)\) and \(−9(−6)\).
Factoring Trinomials of the Form \(x^2+bx+c\)
You have already learned how to multiply binomials using FOIL. Now you’ll need to “undo” this multiplication. To factor the trinomial means to start with the product, and end with the factors.
To figure out how we would factor a trinomial of the form \(x^2+bx+c\), such as \(x^2+5x+6\) and factor it to \((x+2)(x+3)\), let’s start with two general binomials of the form \((x+m)\) and \((x+n)\).
| \((x+m)(x+n)\) | |
|---|---|
| Foil to find the product. | \(x^{2}+m x+n x+m n\) |
| Factor the GCF from the middle terms. | \(x^{2}+(m+n) x+m n\) |
| Our trinomial is of the form \(x^2+bx+c\). | \(\underbrace{x^{2}+(m+n) x+m n}_{\color{red}x^{2}+b x+c}\) |
This tells us that to factor a trinomial of the form \(x^2+bx+c\), we need two factors \((x+m)\) and \((x+n)\) where the two numbers \(m\) and \(n\) multiply to \(c\) and add to \(b\).
Factor \(x^2+11x+24\).
Solution
| \(x^2+11x+24\) | ||||||
|---|---|---|---|---|---|---|
| Write the factors as two binomials with first terms \(x\). | Write two sets of parentheses and put \(x\) as the first term. |
\(\quad x^2+11x+24\) \(=\underbrace{(x+\square)}_{(x+m)}\underbrace{(x+\square)}_{(x+n)}\) |
||||
| Identify \(b\) and \(c\). | \(\underbrace{x^2+11x+24}_{ax^2+bx+c}\) |
\(b=11\) \(c=24\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find two numbers \(m\) and \(n\) that multiply to \(24\) and add to \(11\).
\(\begin{cases} mn&=24\\ m+n&=11\end{cases}\)
|
\(m=3\) \(n=8\) |
||||
| Use \(m\) and \(n\) as the last terms of the factors. | Use \(3\) and \(8\) as the last terms of the binomials. | \(\underbrace{(x+3)}_{(x+m)}\underbrace{(x+8)}_{(x+n)}\) | ||||
| Check by multiplying the factors. |
\(\quad (x+3)(x+8)\) \(=x^2+8x+3x+24\) \(=x^2+11x+24\quad \checkmark\) |
|||||
| Conclude. | The factorization is \((x+3)(x+8).\) | |||||
Factor \( q^2+10q+24\).
- Answer
-
The factorization is \((q+4)(q+6)\).
Factor \(t^2+14t+24\).
- Answer
-
The factorization is \((t+2)(t+12)\).
Let’s summarize the steps we used to find the factors.
- Write the factors as two binomials with first terms \(x\). \(\quad \begin{array} {l} x^2+bx+c \\ (x+\square)(x+\square) \end{array} \)
- Find two numbers \(m\) and \(n\) that
- multiply to \(c\): \(\quad mn=c\)
- add to \(b\): \(\quad m+n=b\)
- Use \(m\) and \(n\) as the last terms of the factors. \(\quad (x+m)(x+n)\)
- Check by multiplying the factors.
In the first example, all terms in the trinomial were positive. What happens when there are negative terms? Well, it depends which term is negative. Let’s look first at trinomials with only the middle term negative.
How do you get a positive product and a negative sum? We use two negative numbers.
Factor \(y^2−11y+28\).
Solution
| \(y^2−11y+28\) | |||||
|---|---|---|---|---|---|
| Write the factors as two binomials with first terms \(y\). |
\(\quad y^2−11y+28\) \(=\underbrace{(y+\square)}_{(y+m)}\underbrace{(y+\square)}_{(y+n)}\) |
||||
| Identify \(b\) and \(c\). |
\(\quad\underbrace{y^2−11y+28}_{ay^2+by+c}\) \(b=-11\) \(c=28\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find \(m\) and \(n\) such that \(\begin{cases} mn&=28\\ m+n&=-11\end{cases}\)
\(m=-4\) \(n=-7\) |
||||
| Use \(m\) and \(n\) as the last terms of the factors. | \(\underbrace{(y−4)}_{(y+m)}\underbrace{(y−7)}_{(y+n)}\) | ||||
| Check. |
\(\quad (y-4)(y-7)\) \(=y^2-7y-4y+28\) \(=y^2-11y+28\quad\checkmark\) |
||||
| Conclude. | The factorization is \((y-4)(y-7)\). |
Factor \(u^2−9u+18\).
- Answer
-
The factorization is \((u−3)(u−6)\).
Factor \(y^2−16y+63\).
- Answer
-
The factorization is \((y−7)(y−9)\).
Now, what if the last term in the trinomial is negative? Think about FOIL. The last term is the product of the last terms in the two binomials. A negative product results from multiplying two numbers with opposite signs. You have to be very careful to choose factors to make sure you get the correct sign for the middle term, too.
How do you get a negative product and a positive sum? We use one positive and one negative number.
When we factor trinomials, we must have the terms written in descending order—in order from highest degree to lowest degree.
Factor \(2x+x^2−48\).
Solution
| \(2x+x^2−48\) | |||||
|---|---|---|---|---|---|
| First we put the terms in decreasing degree order. | \(x^2+2x−48\) | ||||
| Write the factors as two binomials with first terms \(y\). |
\(\quad x^2+2x−48\) \(=\underbrace{(x+\square)}_{(x+m)}\underbrace{(x+\square)}_{(x+n)}\) |
||||
| Identify \(b\) and \(c\). |
\(\quad\underbrace{x^2+2x−48}_{ax^2+bx+c}\) \(b=2\) \(c=-48\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find \(m\) and \(n\) such that \(\begin{cases} mn&=-48\\ m+n&=2\end{cases}\)
\(m=-6\) \(n=8\) |
||||
| Use \(m\) and \(n\) as the last terms of the factors. | \(\underbrace{(x-6)}_{(x+m)}\underbrace{(x+8)}_{(x+n)}\) | ||||
| Check. |
\(\quad (x-6)(x+8)\) \(=x^2+8x-6x-48\) \(=x^2+2x-48\quad\checkmark\) |
||||
| Conclude. | The factorization is \((x-6)(x+8)\). |
Factor \(9m+m^2+18\).
- Answer
-
The factorization is \((m+3)(m+6)\).
Factor \(−7n+12+n^2\).
- Answer
-
The factorization is \((n−3)(n−4)\).
Sometimes you’ll need to factor trinomials of the form \(x^2+bxy+cy^2\) with two variables, such as \(x^2+12xy+36y^2\). The first term, \(x^2\), is the product of the first terms of the binomial factors, \(xx\). The \(y^2\) in the last term means that the second terms of the binomial factors must each contain \(y\).
Factor \(r^2−8rs−9s^2\).
Solution
| \(r^2−8rs−9s^2\) | |||||
|---|---|---|---|---|---|
| Write the factors as two binomials with \(r\) in the first term of each binomial and \(s\) in the second term. |
\(\quad r^2−8rs−9s^2\) \(=\underbrace{(r+\square s)}_{(r+ms)}\underbrace{(r+\square s)}_{(r+ns)}\) |
||||
| Identify \(b\) and \(c\). |
\(\quad\underbrace{r^2−8rs−9s^2}_{ar^2+brs+cs^2}\) \(b=-8\) \(c=-9\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find \(m\) and \(n\) such that \(\begin{cases} mn&=-9\\ m+n&=-8\end{cases}\)
\(m=1\) \(n=-9\) |
||||
| Use \(m\) and \(n\) as the last terms of the factors. | \(\underbrace{(r+s)}_{(r+ms)}\underbrace{(r-9s)}_{(r+ns)}\) | ||||
| Check. |
\(\quad (r+s)(r-9s)\) \(=r^2-9rs+rs-9s^2\) \(=r^2-8rs-9s^2\quad\checkmark\) |
||||
| Conclude. | The factorization is \((r+s)(r-9s).\) |
Factor \(a^2−11ab+10b^2\).
- Answer
-
The factorization is \((a−b)(a−10b)\).
Factor \(m^2−13mn+12n^2\).
- Answer
-
The factorization is \((m−n)(m−12n)\).
Some trinomials are prime. The only way to be certain a trinomial is prime is to list all the possibilities and show that none of them work.
Factor \(u^2−9uv−12v^2\).
Solution
| \(u^2−9uv−12v^2\) | |||||
|---|---|---|---|---|---|
| Write the factors as two binomials with \(u\) in the first term of each binomial and \(v\) in the second term. |
\(\quad u^2−9uv−12v^2\) \(=\underbrace{(u+\square v)}_{(u+mv)}\underbrace{(u+\square v)}_{(u+nv)}\) |
||||
| Identify \(b\) and \(c\). |
\(\quad\underbrace{u^2−9uv−12v^2}_{au^2+buv+cn^2}\) \(b=-9\) \(c=-12\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find \(m\) and \(n\) such that \(\begin{cases} mn&=-12\\ m+n&=-9\end{cases}\)
Note there are no factor pairs that give us \(-9\) as a sum. |
||||
| Conclude. | The trinomial is prime. |
Factor \(x^2−7xy−10y^2\).
- Answer
-
The trinomial is prime.
Factor \(p^2+15pq+20q^2\).
- Answer
-
The trinomial is prime.
Let’s summarize the method we just developed to factor trinomials of the form \(x^2+bx+c\).
When we factor a trinomial, we look at the signs of its terms first to determine the signs of the binomial factors.
|
\( x^{2}+b x+c \) \(= (x+m)(x+n)\) |
|
| \( b \) positive | \( b \) negative |
| \( m,n \) positive | \( m,n \) negative |
| When \( c \) is positive, \( m \) and \( n \) have the same sign. | |
|
For example, \( x^{2}+5 x+6 =(x+2)(x+3).\) |
For example, \(x^2-6x+8= (x-4)(x-2).\) |
| When \( c \) is negative, \( m \) and \( n \) have the opposite sign. | |
|
For example, \( x^2+x-12=(x+4)(x-3). \) |
For example, \(x^2-2x-15= (x-5)(x+3). \) |
Notice that, in the case when \(m\) and \(n\) have opposite signs, the sign of the one with the larger absolute value matches the sign of \(b\).
Factoring Trinomials of the Form ax2 + bx + c Using Trial and Error
Our next step is to factor trinomials whose leading coefficient is not 1, trinomials of the form \(ax^2+bx+c\).
Remember to always check for a GCF first! Sometimes, after you factor the GCF, the leading coefficient of the trinomial becomes \(1\) and you can factor it by the methods we’ve used so far. Let’s do an example to see how this works.
Factor \(4x^3+16x^2−20x\).
Solution
| \(4x^3+16x^2−20x\) | |||||
|---|---|---|---|---|---|
| What is the greatest common factor? | The GCF is \(4x\). | ||||
| Factor it. | \(\quad 4x(x^2+4x−5)\) | ||||
| Is the GCF multiplied by a binomial, a trinomial, or a polynomial with more than three terms? | \(=\underbrace{4x}_{\text{GCF}}\underbrace{(x^2+4x−5)}_{\text{trinomial}}\quad\quad\) It is a trinomial. | ||||
| “Undo FOIL.” Write the trinomial as factors of two binomials with first terms \(x\). | \(=\underbrace{4x}_{\text{GCF}}\underbrace{(x^2+4x−5)}_{(x+\square)(x+\square)}\) | ||||
| Identify \(b\) and \(c\). |
\(=\underbrace{4x}_{\text{GCF}}\underbrace{(x^2+4x−5)}_{ax^2+bx+c}\) \(b=4\) \(c=-5\) |
||||
|
Find two numbers \(m\) and \(n\) that multiply to \(c\) and add to \(b\). \(\begin{cases} mn&=c\\ m+n&=b\end{cases}\) |
Find \(m\) and \(n\) such that \(\begin{cases} mn&=-5\\ m+n&=4\end{cases}\)
\(m=-1\) \(n=4\) |
||||
| Use \(m\) and \(n\) as the last terms of the factors. | \(\underbrace{4x}_{\text{GCF}}\underbrace{(x-1)(x+4)}_{(x+m)(x+n)}\) | ||||
| Check. |
\(\quad 4x(x-1)(x+5)\) \(=4x(x^2+5x-x-5\) \(=4x(x^2+4x-5)\) \(=4x^3+16x^2-20x\quad\checkmark\) |
||||
| Conclude. | The factorization is \(4x(x-1)(x+5)\). |
Factor \(5x^3+15x^2−20x\).
- Answer
-
The factorization is \(5x(x−1)(x+4)\).
Factor \(6y^3+18y^2−60y\).
- Answer
-
The factorization is \(6y(y−2)(y+5)\).
What happens when the leading coefficient is not \(1\) and there is no GCF? There are several methods that can be used to factor these trinomials. First we will use the Trial and Error method.
Let’s factor the trinomial \(3x^2+5x+2\).
From our earlier work, we expect this will factor into two binomials.
\[3x^2+5x+2\nonumber\]\[(\quad)(\quad)\nonumber\]
We know the first terms of the binomial factors will multiply to give us \(3x^2\). The only factors of \(3x^2\) are \(1x,\space 3x\). We can place them in the binomials.
\[(x+ \quad)(3x+\quad)\nonumber\]
Check: Does \(1x·3x=3x^2\)?
We know the last terms of the binomials will multiply to \(2\). Since this trinomial has all positive terms, we only need to consider positive factors. The only factors of \(2\) are \(1\) and \(2\). But we now have two cases to consider as it will make a difference if we write \(1\), \(2\) or \(2\), \(1\) (the opposites are also a possibility, but since the middle term is possitive, we can disregard this possibility).
\[(x+1)(3x+2)\text{ or }(x+2)(3x+1)\nonumber\]
Which factors are correct? To decide that, we multiply the inner and outer terms.
\[ 3x^2+5x+2\text{ or }3x^2+7x+2.\nonumber\]
Since the middle term of the trinomial is \(5x\), the factors in the first case will work. Let’s use FOIL to check.
\[(x+1)(3x+2)\nonumber\]\[3x^2+2x+3x+2\nonumber\]\[3x^2+5x+2\checkmark\nonumber\]
Our result of the factoring is:
\[3x^2+5x+2\nonumber\]\[(x+1)(3x+2)\nonumber\]
Factor \(3y^2+22y+7\) using trial and error.
Solution
Factor \(2a^2+5a+3\) using trial and error.
- Answer
-
The factorization is \((a+1)(2a+3)\).
Factor \(4b^2+5b+1\) using trial and error.
- Answer
-
The factorization is \((b+1)(4b+1)\).
- Write the trinomial in descending order of degrees as needed.
- Factor any GCF.
- Find all the factor pairs of the first term.
- Find all the factor pairs of the third term.
- Test all the possible combinations of the factors until the correct product is found.
- Check by multiplying.
Remember, when the middle term is negative and the last term is positive, the signs in the binomials must both be negative.
Factor \(6b^2−13b+5\) using trial and error.
Solution
| The trinomial is already in descending order. | \(6b^2−13b+5\) |
| Find the factors of the first term. |  |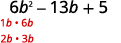
| Find the factors of the last term. Consider the signs. Since the last term, \(5\), is positive its factors must both be positive or both be negative. The coefficient of the middle term is negative, so we use the negative factors. |
 |
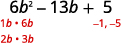Consider all the combinations of factors.
| \(6b^2−13b+5\) | |
|---|---|
| Possible factors | Product |
| \((b−1)(6b−5)\) | \(6b^2−11b+5\) |
| \((b−5)(6b−1)\) | \(6b^2−31b+5\) |
| \((2b−1)(3b−5)\) | \(6b^2−13b+5^∗\) |
| \((2b−5)(3b−1)\) | \(6b^2−17b+5\) |
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial.} &(2b−1)(3b−5) \\ \text{Check by multiplying:} & \\ \hspace{50mm} (2b−1)(3b−5) & \\ \hspace{47mm} 6b^2−10b−3b+5 & \\ \hspace{50mm} 6b^2−13b+5\checkmark & \end{array} \)
Factor \(8x^2−13x+3\) using trial and error.
- Answer
-
The factorization is \((2x−3)(4x−1)\).
Factor \(10y^2−37y+7\) using trial and error.
- Answer
-
The factorization is \((2y−7)(5y−1)\).
When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.
Factor \(18x^2−37xy+15y^2\) using trial and error.
Solution
| The trinomial is already in descending order. | \(18x^2−37xy+15y^2\) |
| Find the factors of the first term. |  |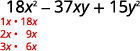
| Find the factors of the last term. Consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative factors. |
 |
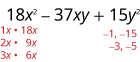Consider all the combinations of factors.
\(\begin{array} {ll} \text{The correct factors are those whose product is} & \\ \text{the original trinomial.} &(2x−3y)(9x−5y) \\ \text{Check by multiplying:} & \\ & \\ & \\ & \\ \hspace{50mm} (2x−3y)(9x−5y) & \\ \hspace{45mm}18x^2−10xy−27xy+15y^2 & \\ \hspace{47mm}18x^2−37xy+15y^2\checkmark & \end{array} \)
Factor \(18x^2−3xy−10y^2\) using trial and error.
- Answer
-
The factorization is \((3x+2y)(6x−5y)\).
Factor \(30x^2−53xy−21y^2\) using trial and error.
- Answer
-
The factorization is \((3x+y)(10x−21y)\).
Don’t forget to look for a GCF first and remember if the leading coefficient is negative, so is the GCF.
Factor \(−10y^4−55y^3−60y^2\) using trial and error.
Solution
| \(\quad −10y^4−55y^3−60y^2\) | |
| Notice the greatest common factor, so factor it first. | \(-5y^2(2y^2+11y+12)\) |
| Factor the trinomial. |  |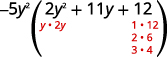
Consider all the combinations.
-
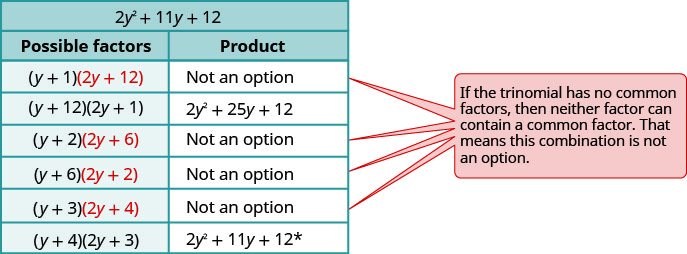
\(\begin{array} {ll} \text{The correct factors are those whose product} & \\ \text{is the original trinomial. Remember to include} & \\ \text{the factor }−5^y2. &−5y^2(y+4)(2y+3) \\ \text{Check by multiplying:} & \\ \hspace{50mm} −5y^2(y+4)(2y+3) & \\ \hspace{45mm} −5y^2(2y^2+8y+3y+12) & \\ \hspace{47mm}−10y^4−55y^3−60y^2\checkmark & \end{array} \)
Factor \(15n^3−85n^2+100n\) using trial and error.
- Answer
-
The factorization is \(5n(n−4)(3n−5)\).
Factor \(56q^3+320q^2−96q\) using trial and error.
- Answer
-
The factorization is \(8q(q+6)(7q−2)\).
Factoring Trinomials of the Form \(ax^2+bx+c\) Using the “\(ac\)” Method
Another way to factor trinomials of the form \(ax^2+bx+c\) is the “\(ac\)” method. (The “\(ac\)” method is sometimes called the grouping method.) The “\(ac\)” method is actually an extension of the methods you used in the last section to factor trinomials with leading coefficient one. This method is very structured (that is step-by-step), and it always works!
Factor \(6x^2+7x+2\) using the “\(ac\)” method.
Solution
Factor \(6x^2+13x+2\) using the “\(ac\)” method.
- Answer
-
The factorization is \((x+2)(6x+1)\).
Factor \(4y^2+8y+3\) using the “\(ac\)” method.
- Answer
-
The factorization is \((2y+1)(2y+3)\).
The “\(ac\)” method is summarized here.
- Factor any GCF.
- Find the product \(ac\).
- Find two numbers \(m\) and \(n\) that:
\(\begin{array} {ll} \text{Multiply to }ac &mn=ac \\ \text{Add to }b &m+n=b \\ &ax^2+bx+c \end{array} \) - Split the middle term using \(m\) and \(n\). \(ax^2+mx+nx+c\)
- Factor by grouping.
- Check by multiplying the factors.
Don’t forget to look for a common factor!
Factor \(10y^2−55y+70\) using the ‘“\(ac\)” method.
Solution
| \(10y^2−55y+70\) | ||
|---|---|---|
| Is there a greatest common factor? | Yes, the GCF is \(5\). | |
| Factor it. | \(5(\underbrace{2y^2-11y+14}_{ax^2+bx+c}\) | |
|
The trinomial inside the parentheses has a leading coefficient that is not \(1\). Find the product \(ac\). |
\(ac=28\) | |
| Find two numbers that multiply to \(ac\) and add to \(b\). |
\((−4)(−7)=28\) \((-4)+(-7) = -11\) |
|
| Split the middle term. |
\(5(2y^2-7y-4y+14)\)
|
|
| Factor the trinomial by grouping. | \(5(y-2)(2y-7)\) | |
| Check by multiplying all three factors |
\(\quad 5(y−2)(2y−7)\) \(=5(2y^2−7y−4y+14)\) \(= 5(2y^2−11y+14)\) \(=410y^2−55y+70\checkmark\) |
|
| Conclude. | The factorization is \(5(y-2)(2y-7)\). |
Factor \(16x^2−32x+12\) using the “\(ac\)” method.
- Answer
-
The factorization is \(4(2x−3)(2x−1)\).
Factor \(18w^2−39w+18\) using the “\(ac\)” method.
- Answer
-
The factorization is \(3(3w−2)(2w−3)\).
Factoring Using Substitution (optional)
Sometimes a trinomial does not appear to be in the \(ax^2+bx+c\) form. However, we can often make a thoughtful substitution that will allow us to make it fit the \(ax^2+bx+c\) form. This is called factoring by substitution. It is standard to use \(u\) for the substitution.
In the \(ax^2+bx+c\), the middle term has a variable, \(x\), and its square, \(x^2\), is the variable part of the first term. Look for this relationship as you try to find a substitution.
Factor \(x^4−4x^2−5\) by substitution (just using integers).
Solution
The variable part of the middle term is \(x^2\) and its square, \(x^4\), is the variable part of the first term. (We know \((x^2)^2=x^4)\). If we let \(u=x^2\), we can put our trinomial in the \(ax^2+bx+c\) form we need to factor it.
| \(\quad x^4−4x^2−5\) | |
| Rewrite the trinomial to prepare for the substitution. | \(=(x^2)^2-4(x^2)-5\) |
| Let \(u=x^2\) and substitute. | \(=u^2-4u-5\) |
| Factor the trinomial. | \(=(u+1)(u-5)\) |
| Replace \(u\) with \(x^2\). | \(=(x^2+1)(x^2-5)\) |
| Check: |
\(\begin{array} {l} \hspace{37mm} (x^2+1)(x^2−5) \\ \hspace{35mm}x^4−5x^2+x^2−5 \\ \hspace{40mm}x^4−4x^2−5\checkmark\end{array}\) |
Factor \(h^4+4h^2−12\) by substitution (just using integers).
- Answer
-
The factorization is \((h^2−2)(h^2+6)\).
Factor \(y^4−y^2−20\) by substitution (just using integers).
- Answer
-
The factorization is \((y^2+4)(y^2−5)\).
Sometimes the expression to be substituted is not a monomial.
Factor \((x−2)^2+7(x−2)+12\) by substitution.
Solution
The binomial in the middle term, \((x−2)\) is squared in the first term. If we let \(u=x−2\) and substitute, our trinomial will be in \(ax^2+bx+c\) form.
| \(\quad (x−2)^2+7(x−2)+12\) | |
|---|---|
| Rewrite the trinomial to prepare for the substitution. |
\(={\color{red}{(x-2)}}^2 +7{\color{red}{(x-2)}}+12\) |
| Let \(u=x−2\) and substitute. |
\(= {\color{red}{u}}^2+7{\color{red}{u}}+12\) |
| Factor the trinomial. |
\(=(u+3)(u+4)\) |
| Replace \(u\) with \(x−2\). |
\(=((x-2)+3)((x-2)+4)\) |
| Simplify inside the parentheses. |
\(=(x+1)(x+2)\) |
This could also be factored by first multiplying out the \((x−2)^2\) and the \(7(x−2)\) and then combining like terms and then factoring. Most students prefer the substitution method.
Factor \((x−5)^2+6(x−5)+8\) by substitution.
- Answer
-
The factorization is \((x−3)(x−1)\).
Factor \((y−4)^2+8(y−4)+15\) by substitution.
- Answer
-
The factorization is \((y−1)(y+1)\).
- Holly factored \((x^2−x−20)(x^2−x−20)\) as \((x+5)(x−4)(x+5)(x−4)\). Ariane factored it as \((x+4)(x−5)(x+4)(x−5)\). Lin factored it as \((x−5)(x−4)(x−5)(x−4)\). Who is correct? Explain why the other two are wrong.
- How can you check whether you have factored correctly?
- Create a multiple choice factoring question for a trinomial of degree 2 with leading coefficient different from 1 and provide the answer. (Make the incorrect choices so that they might capture a mistake that someone might make).
- Is it possible to factor a trinomial of degree 2 with leading coefficient different from 1 into a monomial and a binomial?
- Do you prefer the guess and check method or the 'ac'-method? Explain.
- Explain with an example why the ac- method works.
Factor \(6x^2z^2-31xz^2+35z^2\).
Key Concepts
- How to factor trinomials of the form \(x^2+bx+c\).
- Write the factors as two binomials with first terms x. \(\quad \begin{array}{l} x^2+bx+c \\ (x\quad)(x\quad)\end{array}\)
- Find two numbers \(m\) and \(n\) that
\(\begin{array} {ll} \text{multiply to} &c,\space m·n=c \\ \text{add to} &b,\space m+n=b\end{array}\) - Use \(m\) and \(n\) as the last terms of the factors. \(\qquad (x+m)(x+n)\)
- Check by multiplying the factors.
- Strategy for Factoring Trinomials of the Form \(x^2+bx+c\): When we factor a trinomial, we look at the signs of its terms first to determine the signs of the binomial factors.
For trinomials of the form: \(x^2+bx+c = (x+m)(x+n)\)
When \(c\) is positive, \(m\) and \(n\) must have the same sign (and this will be the sign of \(b\)).
Examples: \(x^2+5x+6=(x+2)(x+3)\), \(x^2−6x+8 = (x−4)(x−2)\)
When \(c\) is negative, \(m\) and \(n\) have opposite signs. The larger of \(m\) and \(n\) will have the sign of \(b\).
Examples: \(x^2+x−12=(x+4)(x−3)\), \(x^2−2x−15=(x−5)(x+3)\)
Notice that, in the case when \(m\) and \(n\) have opposite signs, the sign of the one with the larger absolute value matches the sign of \(b\). - How to factor trinomials of the form \(ax^2+bx+c\) using trial and error.
- Write the trinomial in descending order of degrees as needed.
- Factor any GCF.
- Find all the factor pairs of the first term.
- Find all the factor pairs of the third term.
- Test all the possible combinations of the factors until the correct product is found.
- Check by multiplying.
- How to factor trinomials of the form \(ax^2+bx+c\) using the “\(ac\)” method.
- Factor any GCF.
- Find the product \(ac\).
- Find two numbers \(m\) and \(n\) that:
\(\begin{array} {ll} \text{Multiply to }ac. &m·n=a·c \\ \text{Add to }b. &m+n=b \\ &ax^2+bx+c\end{array}\) - Split the middle term using \(m\) and \(n\). \(\quad ax^2+mx+nx+c\)
- Factor by grouping.
- Check by multiplying the factors.