2.1: Linear Equations

Last updated
Save as PDF

Page ID: 96380

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Understand what it means to solve a linear equation.
Solve linear equations with one unknown, i.e., one-variable.

Be Prepared

Before you get started, take this readiness quiz.

Simplify $3(2+x)$.
Simplify $\dfrac{1}{3}+\dfrac{9}{4}\cdot \dfrac{5}{7}$.
Is the expression $9 x^{2}-12 x+4$ linear?

Introduction to Equations

In this unit we will use these expressions in applications!In the previous unit we used expressions to represent quantities when it involved a quantity that is either unknown or could be any of a number of values. For example, we may want to represent the total amount of money in a bin that had 5 dollars and a certain number of quarters. How could we do this? We first did some examples where we chose a specific number of quarters:

If we had 3 quarters then we have $\$ 5.75$. If the bin contains 7 quarters then the bin has $\$ 5+1.75=\$ 6.75$. Using this as an example, we can try to discover what we do if we don't know how many quarters we are dealing with. We let the variable $q$ represent the number of quarters. Then we can translate the sum made by having $q$ quarters: $\dfrac{q}{4}$. We can test this on our 7 quarters: $\dfrac{7}{4}=1.75$. To then find the total in the bin we add the 5 dollars. So the total amount in the bin is $5+q/4.$

We can test this on 3 quarters:

\[5+\dfrac{3}{4}=5.75\]

and on 7 quarters:

\[5+\dfrac{7}{4}=5+1.75=6.75.\]

But in this unit, we recognize this expression represents the amount of money in the bin no matter what $q$ is and we use this fact to solve problems. For example, suppose we know that the money in the bin is equal to $\$8.25$ and we want to know how many quarters there are. Then we represent the amount of money in the bin in two ways which then must be equal (since they represent the same quantity):

$8.25=5+\dfrac{q}{4}.$

This is an assertion about $q$. Sometimes we have used equal signs during a simplification of an expression. Such equal signs implicitly mean that equation holds for all values of the variables except those that leave an expression undefined. In the case of this equation and others in this unit, these equalities say something about the variable, and for 'most' values of the variable the equation is false. We will seek the values which make the equality true, .i.e., we seek to solve these equations.

We can imagine ourselves looking at this bin and putting aside the $\$5$. We then know that what is left is both $3.25$ and $\dfrac{q}{4}$, so that the contribution of the quarters is $\$3.25$ which we can figure out using our experience with counting money that there are $13$ quarters.

The expression $5+\dfrac{q}{4}$ has two basic interpretations: If there are several such bins then we could use the expression $5+\dfrac{q}{4}$ and substitute the number of quarters, one at a time, in for $q$ to find the total amount of money in each bin; or maybe, for example we have only one bin but someone will tell us later how many quarters are in the bin and we will use this expression, substituting what they tell us for $q$, to find out how much money is in that bin. The latter interpretation is what was used above. We know there were a certain but currently unknown number of quarters in the bin. Combining this with the information that the total amount of money in the bin was $\$8.25$ we learned what $q$ must be.

The above is just a simple example to illustrate the basic notions we will be using in this section. We will do many examples with the expressions we used in the last unit. Before continuing, make sure you understand this most simple example.

Linear Equations and Their Solutions

Just as linear expressions are the simplest expressions involving only multiplication and addition of numbers, here we consider equations involving these expressions.

We begin by returning to the example in the introduction and considering the 'solution.'

You may be familiar with how to solve this equation, but the basics of solving equations lie in this one example.

Recall that in the example we had a bin with 5 dollars and a certain number of quarters. We arrived at an expression equal to the amount of money in the bin once the number of quarters (which we will call '$q$') is known and substituted. The expression is

$5+\dfrac{q}{4}.$

The question raised in the introduction was to suppose we know something about the amount of money in the bin, namely, that it contains $\$8.25$ and we want to find the number of quarters. We wrote the amount of money in two ways (which then must be equal!). On the one hand we know the bin contains $\$8.25$ and on the other hand we know that if it has $q$ quarters, it has $5+\dfrac{q}{4}.$ dollars. So,

$8.25=5+\dfrac{q}{4}.$

We figured out how many quarters there are (13) using our heads and experience. Here, we would like to proceed differently so that it sets the stage for more complicated problems.

The equality $8.25=5+\dfrac{q}{4}.$ means that if we substitute the number of quarters in for the variable $q$, we have a true statement. We already saw that there are 13 quarters and we see that

$8.25=5+\dfrac{q}{4}.$

	$5+q/4$
	$=5+13/4$
	$=5+3.25$
	$=8.25$
So,	$8.25=5+13/4,$ or $8.25=5+q/4,$ when $q=13$.

We say that $8.25=5+\dfrac{q}{4}$ is an equation with one variable and $q=13$ is a solution. This equation is in fact a linear equation since the expressions on both sides are linear expressions.

This is a verification of the solution. If we were unable to figure this out by using our experience, how could we find the solution?

Notice that we are interested in finding $q$. If we knew what $q$ was we could evaluate $q$ by first dividing by 4 and then adding the result to 5. Here we must use the order of operations. So to undo these actions, we must undo them in the opposite order. And to maintain the truth of the equation, we must do the same thing to both sides.

$8.25=5+\dfrac{q}{4}.$

The last thing we do to evaluate the right side is add 5. This is the first thing we undo! How do we undo addition? Subtraction! So let's subtract 5 on both sides of the equation.

$8.25-5=5+\dfrac{q}{4}-5,$

or, simplifying,

$3.25=\dfrac{q}{4}.$

Next, $q$ is being divided by 4 and we must undo this division to 'get at' $q$. So, what is the opposite of the action of division? Multiplication! So, lets multiply both sides (to maintain the truth of the equality) of the equation by 4.

$3.25\cdot 4=\dfrac{q}{4}\cdot 4$

so,

$(3+1/4)\cdot 4=\dfrac{q}{4}\cdot \dfrac{4}{1}$

and so

$12+1=\dfrac{4q}{4}$

or,

$q=13$.

Note that if you do the arithmetic correctly you should see the operation you are undoing disappearing as you wished!

We have had extensive practice with simplifications in the first unit, so from now on we will just indicate when we have simplified.

We introduce some general vocabulary:

Definition

An equation is a mathematical sentence of the form (an expression)$=$ (another expression).

A solution to an equation in a variable (lets call it $x$) is a number that we can substitute in for $x$ that makes the equation true.

Two equations are equivalent if they have the same solutions.

Finding the solutions of an equation is called solving the equation.

Definition

A linear equation with one variable $x$ is an equation that is equivalent to an equation $Ax+B=0$, where $A\not= 0$.

To solve a linear equation with one variable means to find the number that when substituted makes the equation true. If $a$ is a solution to the equation with the variable $x$, then we may also say $x=a$, is a solution (it is a simplification of the original assertion).

Example $\PageIndex{4}$

Why is the equation $5=3x-2$ linear? Solve the equation.

Solution

The equation is linear because both sides can be written in the form $ax+b$ and so are linear expressions. We note that for most values of $x$ the equation is not satisfied.

Is $x=1$ a solution?	Does $5=3(1)-2$? That is, does $5=1?$ No. So $x=1$ is not a solution.
Is $x=-2$ a solution?	Does $5=3(-2)-2$? That is, does $5=-8?$ No. So $x=1$ is not a solution.

What is the solution then? Or maybe there is more than one?

The assertion about $x$ is that if we multiply by 3 and then subtract 2 from the result, we should get 5. We need to undo this in the reverse order. And, to preserve the equality, whatever we do to one side of the equal sign we must do to the other. We need to write an equivalent equation of the form $x=a$, that is, to see to it that $x$ is on one side of an equation and a number is on the other side.

	\(5=3x-2\)
The opposite of subtracting 2 is adding 2. So we now add 2 to both sides.	\(5+2=3x-2+2\), or \(7=3x\)
The \(x\) is being multiplied by 3 and to undo multiplication, we must divide!	\(7/3=3x/3\) or \(x=7/3\)
We may check to see that our conclusion about \(x\) is true.	\(3(7/3)-2=7-2=5\) So the equation is indeed true!

$5=3x-2$

The opposite of subtracting 2 is adding 2. So we now add 2 to both sides.

$5+2=3x-2+2$, or $7=3x$

The $x$ is being multiplied by 3 and to undo multiplication, we must divide!

$7/3=3x/3$ or $x=7/3$

We may check to see that our conclusion about $x$ is true.

$3(7/3)-2=7-2=5$

So the equation is indeed true!

We see that by undoing the actions on $x$, we were led to the conclusion that $x$ must be 7/3. So there is only one solution!

Try It $\PageIndex{5}$

Why is the equation $2x+5=3$ linear? Solve the equation.

Answer: Answers vary. $x=-1$

Try It $\PageIndex{6}$

Why is the equation $2m+5=-m+3$ linear? Solve the equation. Note that you can do anything to both sides of the equation to get your desired outcome!

Answer: Answers vary. $m=-2/3 $

Example $\PageIndex{7}$

The perimeter of an enclosed rectangle is 60 feet. The length is twice six more than the width. What are the dimensions of the enclosure?

Solution

Let's start with some example to understand the relation between the width and the length. If the width is 4 feet, for example, and the length is twice (six more than the width), then the length is 2 times 10 feet or, 20 feet. Since this leads to a perimeter of 20+4+20+4=48 feet (which isn't the correct perimeter, but has the correct width/length relation). We see here also that our answer should have a width larger than 4 feet since the perimeter of 48 feet is less than the required 60 feet. If the width is 10 feet, then the length is twice (six more than the width), or twice 16 feet, or, 32 feet. The perimeter in this example will be greater than 64 so the width here is too long. But we can use our examples to lead us to write down an expression for the length if $w$ stands for the unknown width. The length is twice (six more than the width), or twice (6+$w$). Now we can't actually add since we don't know what $w$ is, but we can still multiply by 2 to get that the length is $2(6+w)$. We indicate this on a picture. This picture is only to help us with relationships and will very likely not have the final length or width correct!

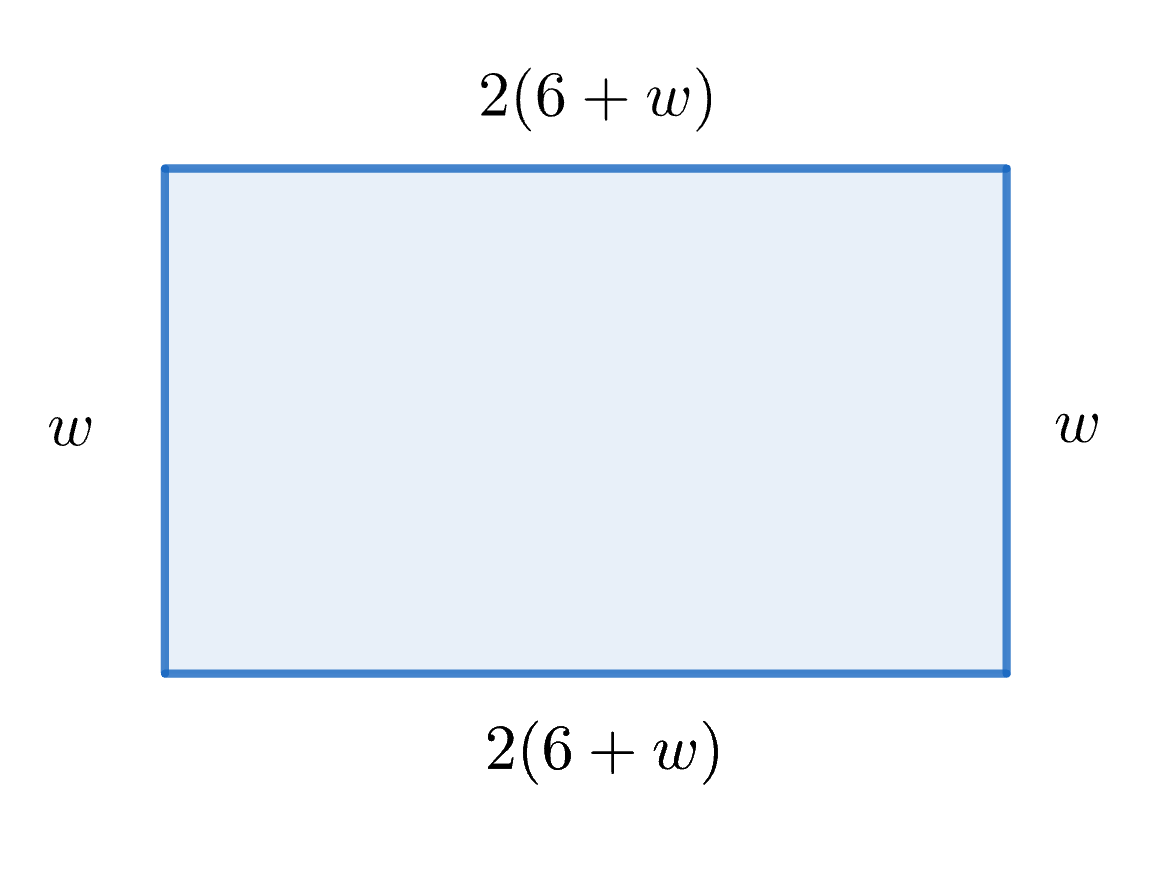$geogebra-export (5).png$

So, we know then that the perimeter for the width $w$ we are looking for is

$w+2(6+w)+w+2(6+w)=2w+4(6+w).$

We know that the perimeter is also 60 feet, so 60 must be equal to the expression above for the $w$ we seek:

$60= 2w+4(6+w).$

We can use our skills of simplifying to rewrite the right side to get the equivalent equation

	$60= 2w+4(6+w)$
	$60= 2w+24+4w$
	$60= 6w+24$

Notice that the right hand side says to multiply $w$ by 6 and then add 24. To undo these actions we must undo them in the opposite order!

Now, the two sides of this equation are equal for the $w$ we are looking for, so the equality is preserved if we subtract 24 from both sides.

This gives us:

$60-24= 6w+24-24$, or, simplifying both sides, $36= 6w.$

We can then divide both sides by 6 and since 36 is the same as $6w$ for the $w$ we are looking for, dividing both sides by 6 will result in an equality:

$36/6= 6w/6$, or, $w=6 \;\mathrm{feet}$.

We recall that the length is $2(6+w)=2(6+6)=24$ feet.

So the rectangular enclosure has a width of 6 feet and a length of 24 feet.

(We can check that the length is twice six more than the width and that the perimeter is 60 feet).

Try It $\PageIndex{8}$

The perimeter of an enclosed isosceles triangle is 40 feet. The length of the shortest side is 7 less than half of the two longest (equal) sides. What are the length of the sides of the enclosure? Give some examples of any expression you develop and write your solution in detail.

Answer: Answers vary. $94/5\; \mathrm{ft}, 94/5 \;\mathrm{ft}, 12/5\; \mathrm{ ft} .$

Writing Exercises $\PageIndex{9}$

How do you recognize a linear equation?
Give an example of a linear equation.
Do all linear equations have a solution?
Explain the relationship between the order of operations and the process of solving $3x-4=7$.

Exit Problem

A rectangular garden has a length the is 10 feet longer than its width. The perimeter is 42 feet. What are the dimensions of the garden?

Key Concepts

Linear equation

Solution to a linear equation

Solving a linear equation

	\(5+q/4\)
	\(=5+13/4\)
	\(=5+3.25\)
	\(=8.25\)
So,	\(8.25=5+13/4,\) or \(8.25=5+q/4,\) when \(q=13\).

Is \(x=1\) a solution?	Does \(5=3(1)-2\)? That is, does \(5=1?\) No. So \(x=1\) is not a solution.
Is \(x=-2\) a solution?	Does \(5=3(-2)-2\)? That is, does \(5=-8?\) No. So \(x=1\) is not a solution.

Search

Definition

Definition

Example \(\PageIndex{4}\)

Solution

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Try It \(\PageIndex{8}\)

Writing Exercises \(\PageIndex{9}\)

Exit Problem

	\(60= 2w+4(6+w)\)
	\(60= 2w+24+4w\)
	\(60= 6w+24\)