2.5: Radical Equations
- Page ID
- 94030
By the end of this section, you will be able to:
- Solve radical equations
- Solve radical equations with two radicals
- Use radicals in applications
Before you get started, take this readiness quiz.
- Simplify \((y−3)^{2}\).
- Solve \(2x−5=0\).
- Solve \(n^{2}−6n+8=0\).
Radical Equations
In this section we will solve equations that have a variable in the radicand of a radical expression. An equation of this type is called a radical equation.
An equation in which a variable is in the radicand of a radical expression is called a radical equation.
As always, these equations arise as assertions about an unknown quantity. It becomes the task then to solve these equations. Radicals sometimes arise in geometric problems which we will talk more about in the next unit. We can talk about those coming from the Pythagoras' Theorem, or the resulting distance formula.
.png?revision=1&size=bestfit&width=517&height=250)
Suppose for example you know that a boat is 10 meters further from an observer at a light house than the it is from the shore and the observer is 80 meters from the point on the shore that is closest to boat. Suppose that the triangle that is formed by the observer, the boat, and the point on the shore closest to the boat is a right triangle where the hypotenuse is formed by the segment connecting the observer to the boat. How close is the boat to the shore? There are ways to arrive at an equation without radicals, but you may also do the following:
First call the distance from the boat to the shore \(d\). Then we can determine the distance from the observer to the boat is given by
\(\sqrt{80^2+d^2}\),
but we know that this is also \(d+10\) since "boat is 10 meters further from an observer at a light house than the it is from the shore". So for the \(d\) we seek, we see
\(d+10=\sqrt{80^2+d^2}\).
The distance we seek satisfies this equation! So, we must now solve this equation for \(d\).
Notice that the difficulty with this equation is that there is a square root on the right side of the equation. The order of operations says that if we were to evaluate the right side, we would evaluate the square root last. So we try to undo that square root first! What is the opposite of the square root? The square!! So we should square both sides of the equation. Since the two sides of the equation
\(d+10=\sqrt{80^2+d^2}\)
are equal (that is why it's an equation), the squares will also be equal.
So we learn that \(d\) must also satisfy
\((d+10)^2=80^2+d^2.\)
These two equations may not be equivalent since to undo this step we would need to take a square root of both sides and every positive number has two square roots! How would we know which to use? For example, if \(4=sqrt{a}\) then \(a=16\), BUT if \(a^2=16\) then either \(a=\sqrt{16}=4\) or \(a=-\sqrt{16}=-4\).
Now this is an equation which we know how to solve (and which if we had gone about it differently could have arrived at initially),
| \((d+10)^2=80^2+d^2.\) | |
| Distribute on the left side to arrive at | \(d^2+20d+100=80^2+d^2\) |
| Subtract \(d^2\) on both sides (we see that these should cancel!!) |
\(d^2-d^2+20d+100=80^2+d^2-d^2\) or, equivalently, \(20d+100=80^2\) |
| Notice that this is a linear equation and our variable appears on the left side only. So the last step if we evaluated the left side for a particular \(d\) is adding 100, so to undo this we subtract 100 on both sides of the equation to get |
\(20d+100-100=80^2-100\) or, equivalently, \(20d=6300\) |
| And then undoing the multiplication of \(d\) by 20, we divide both sides of the equation by 20 to get |
\(20d/20=6300/20\) or, equivalently, \(d=315\) |
So, the distance we seek is 315 meters. We must check our answer since
while \(d\) satisfies \((d+10)^2=80^2+d^2\),
it must satisfy either
\(d+10=\sqrt{80^2+d^2}\) or \(d+10=-\sqrt{80^2+d^2}\)
but we want to make sure it is
\(d+10=\sqrt{80^2+d^2}\) that it satisfies.
Let's check it!
The left side is \(315+10=316\)
and the right side is \(\sqrt{80^2+315^2}=325\).
So, indeed we found the distance we seek and conclude that the boat is 325 meters from the shore.
Solving Equations with Square Roots
As usual, when solving these equations, what we do to one side of an equation we must do to the other side as well. Once we isolate the square root, our strategy will be to square both sides of the equation. This will eliminate the radical.
Solving radical equations with square roots by squaring both sides may introduce an algebraic solution that would not be a solution to the original radical equation. Again, we call this an extraneous solution. As explained in the context above, the issue is that \(x^2=a\) (where \(a\) is some fixed number) is not equivalent to \(x=\sqrt{a}\), but rather to \(x=\sqrt{a}\) or \(x=-\sqrt{a}\). So is we find a solution to \(x^2=a\) it may be a solution to \(x=-\sqrt{a}\) and not to \(x=\sqrt{a}\) as desired. We therefore must check our answer to see if it is a solution to the equation we wanted to solve originally.
In the next example, we will see how to solve a radical equation. Our strategy is based on squaring a square root. This will eliminate the radical.
For \(a \geq 0\), \(\left(\sqrt{a}\right)^{2}=a\).
This is saying that if we want to undo a square root we need to square (notice where the square and the square-root button are on your calculator)!
Keep the order of operations in mind as you solve equations. We will demonstrate this concept in the next example.
Solve \(\sqrt{5 n-4}-9=0\).
- Solution
- Consider the equation.
-
\(\sqrt{5 n-4}-9=0\) Isolate the radical on one side of the equation. \(\sqrt{5 n-4}-9{\color{red}{\; +\; 9}}=0{\color{red}{ \;+ \;9}}\)
Simplify. \(\sqrt{5 n-4}=9\) Square both sides of the equation. Remember that \(\left(\sqrt{a}\right)^{2}=a\). \(\left(\sqrt{5 n-4}\right)^{2}=(9)^{2}\)
\(5n-4 = 81\)
Solve the new equation. \(\begin{aligned} 5n-4 {\color{red}{\;+\;4}} &= 81{\color{red}{\;+\;4}} \\ 5n &=85\\ n&=\dfrac{85}{5}\\n&=17\end{aligned}\)
Check the answer in the original equation. \(\begin{aligned} \sqrt{5 n-4}-9 &=0\\ \sqrt{5 \cdot {\color{red}{17}}-4}-9 &\stackrel{?}{=} 0\\ \sqrt{85-4}-9&\stackrel{?}{=} 0 \\ \sqrt{81}-9 &\stackrel{?}{=} 0\\9-9&\stackrel{?}{=} 0 \qquad \text{True}\end{aligned}\)
The solution is \(n=17\).
Solve \(\sqrt{3 m+2}-5=0\).
- Answer
-
\(m=\dfrac{23}{3}\)
Solve \(\sqrt{10 z+1}-2=0\).
- Answer
-
\(z=\dfrac{3}{10}\)
- Isolate the radical on one side of the equation.
- Square both sides of the equation.
- Solve the new equation.
- Check the answer in the original equation.
When we use a radical sign, it indicates the principal or positive root. If an equation has a square root equal to a negative number, that equation will have no solution.
Solve \(\sqrt{9 k-2}+1=0\).
- Solution
-
\(\sqrt{9 k-2}+1=0\) Isolate the radical on one side of the equation. \(\sqrt{9 k-2}+1{\color{red}{\;-\;1}}=0 {\color{red}{\;-\;1}}\) Simplify. \(\sqrt{9 k-2}=-1\) Because the square root is equal to a negative number, the equation has no solution.
Solve \(\sqrt{2 r-3}+5=0\).
- Answer
-
no solution
Solve \(\sqrt{7 s-3}+2=0\).
- Answer
-
no solution
If one side of an equation with a square root is a binomial, we use the Product of Binomial Squares Pattern when we square it.
\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
Don't forget the middle term!
Solve \(\sqrt{p-1}+1=p\).
- Solution
-
\(\sqrt{p-1}+1=p\) To isolate the radical, subtract \(1\) from both sides. \(\sqrt{p-1}+1{\color{red}{\;-\;1}}=p{\color{red}{\;-\;1}}\) Simplify. \(\sqrt{p-1}=p-1\) Square both sides of the equation. \(\left(\sqrt{p-1}\right)^2=(p-1)^2\) Simplify, using the Product of Binomial Squares Pattern on the right, then solve the new equation. \(p-1=p^2-2p+1\) It is a quadratic equation, so get zero on one side. \(0=p^2-3p+2\) Factor the right side. \(0=(p-1)(p-2)\)
\((p-1)(p-2)=0\)
Use the Zero Product Property. \(p-1=0\quad\) or \(\quad p-2=0\) Solve each equation. \(p=1\quad\) or \(\quad p=2\) Check the answers. \(\begin{array}{crcl} p={\color{red}{1}} \quad & \sqrt{p-1}+1&=&p \\ & \sqrt{{\color{red}{1}}-1}+1&\stackrel{?}{=}& \color{red}{1} \\ & 0+1&\stackrel{?}{=}&1 \\ &1 &\stackrel{?}{=}&1\qquad\text{True}\end{array} \)
\(\begin{array}{crcl} p={\color{red}{2}} \quad & \sqrt{p-1}+1&=&p \\ & \sqrt{{\color{red}{2}}-1}+1&\stackrel{?}{=}& \color{red}{2} \\ & \sqrt{1}+1&\stackrel{?}{=}&2 \\ &2 &\stackrel{?}{=}&2\qquad\text{True}\end{array} \)
The solutions are \(p=1\) or \(p=2\).
Solve \(\sqrt{x-2}+2=x\).
- Answer
-
\(x=2\) or \(x=3\)
Solve \(\sqrt{y-5}+5=y\).
- Answer
-
\(y=5\) or \(y=6\)
Sometimes the solution of a radical equation results in two algebraic solutions, but one of them may be an extraneous solution!
Solve \(\sqrt{r+4}-r+2=0\).
- Solution
-
\(\sqrt{r+4}-r+2=0\) Isolate the radical. \(\sqrt{r+4}=r-2\) Square both sides of the equation. \((\sqrt{r+4})^{2}=(r-2)^{2}\) Simplify and then solve the equation. If it is a quadratic equation, so get zero on one side. Factor the right side. \(0=r(r-5)\) Use the Zero Product Property. \(0=r\) or \(0=r-5\) Solve the equation. \(r=0 \quad r=5\) Check your answer. \(\begin{array}{crcl} r={\color{red}{0}} \quad & \sqrt{r+4}-r+2&=&0 \\ & \sqrt{ {\color{red}{0}} +4}-{\color{red}{0}}+2&\stackrel{?}{=}& 0 \\ & \sqrt 4+2&\stackrel{?}{=}&0 \\ &4 &\stackrel{?}{=}&0\qquad\text{False}\end{array} \)
\(\begin{array}{crcl} r={\color{red}{5}} \quad & \sqrt{r+4}-r+2&=&0 \\ & \sqrt{ {\color{red}{5}} +4}-{\color{red}{5}}+2&\stackrel{?}{=}& 0 \\ & \sqrt 9-3&\stackrel{?}{=}&0 \\ &0 &\stackrel{?}{=}&0\qquad\text{True}\end{array} \)
\(r=0\) is an extraneous solution.
The solution is \(r=5\).
Solve \(\sqrt{m+9}-m+3=0\).
- Answer
-
\(m=7\)
Solve \(\sqrt{n+1}-n+1=0\).
- Answer
-
\(n=3\)
When there is a coefficient in front of the radical, we must raise it to the power of the index, too.
Solve \(3 \sqrt{3 x-5}-8=4\).
- Solution
-
\(3 \sqrt{3 x-5}-8=4\) Isolate the radical term. \(3 \sqrt{3 x-5}=12\) Isolate the radical by dividing both sides by \(3\). \(\sqrt{3 x-5}=4\) Square both sides of the equation. \((\sqrt{3 x-5})^{2}=(4)^{2}\) Simplify, then solve the new equation. \(3 x-5=16\) \(3x=21\) Solve the equation. \(x=7\) Check the answer. \(\begin{array}{crcl} x={\color{red}{7}} \quad & 3 \sqrt{3 x-5}-8 &=& 4 \\ &3 \sqrt{3 {\color{red}{(7)}}-5}-8 &\stackrel{?}{=}& 4 \\ & 3\sqrt{21-5}-8&\stackrel{?}{=}&4 \\ &3\sqrt{16}-8 &\stackrel{?}{=}&4 \\ & 3(4)-8 &\stackrel{?}{=}& 4\\ &4&\stackrel{?}{=}&4 \qquad\text{True}\end{array} \) The solution is \(x=7\).
Solve \(2 \sqrt{4 a+4}-16=16\).
- Answer
-
\(a=63\)
Solve \(3 \sqrt{2 b+3}-25=50\)
- Answer
-
\(b=311\)
Solve Radical Equations with Two Radicals
If the radical equation has two radicals, we start out by isolating one of them. It often works out easiest to isolate the more complicated radical first.
In the next example, when one radical is isolated, the second radical is also isolated.
Solve \(\sqrt{4 x-3}=\sqrt{3 x+2}\).
- Solution
-
The radical terms are isolated. \(\sqrt{4 x-3}=\sqrt{3 x+2}\) Square both sides of the equation. \(\left(\sqrt{4 x-3}\right)^{2}=\left(\sqrt{3 x+2}\right)^{2}\)
Simplify, then solve the new equation.
\(\begin{aligned} 4x-3 &= 3x+2\\4x-3 {\color{red}{\;-3x\;+\;3}} &= 3x+2 {\color{red}{\;-3x\;+\;3}}\\x&=5\end{aligned}\)
Check the answer. \(\begin{array}{crcl} x={\color{red}{5}} \quad & \sqrt{4 x-3}&=&\sqrt{3 x+2}\\ & \sqrt{4 \cdot {\color{red}{5}} -3}&\stackrel{?}{=}& \sqrt{3 \cdot {\color{red}{5}}+2} \\ & \sqrt{17}&\stackrel{?}{=}&\sqrt{17}\qquad\text{True}\end{array} \) The solution is \(x=5\).
Solve \(\sqrt{5 x-4}=\sqrt{2 x+5}\).
- Answer
-
\(x=3\)
Solve \(\sqrt{7 x+1}=\sqrt{2 x-5}\).
- Answer
-
There is no real solution.
Sometimes after raising both sides of an equation to a power, we still have a variable inside a radical. When that happens, we repeat Step 1 and Step 2 of our procedure. We isolate the radical and square both sides of the equation again.
Solve \(\sqrt{m}+1=\sqrt{m+9}\).
- Solution
-
Isolate one of the radical terms on one side of the equation. The radical on the right is isolated. \(\sqrt{m}+1=\sqrt{m+9}\) Raise both sides of the equation to the power of the index. We square both sides.
Simplify--be very careful as you multiply!
\((\sqrt{m}+1)^{2}=(\sqrt{m+9})^{2}\) Are there any more radicals? If yes, repeat Step 1 and Step 2 again.
If no, solve the new equation.
There is still a radical in the equation.
So we must repeat the previous steps. Isolate the radical term.
Here, we can easily isolate the radical by dividing both sides by \(2\).
Square both sides.
\(\begin{aligned} m+2 \sqrt{m}+1 &=m+9 \\ 2 \sqrt{m} &=8 \\ \sqrt{m} &=4 \\(\sqrt{m})^{2} &=(4)^{2} \\ m &=16 \end{aligned}\) Check the answer in the original equation. \(\begin{aligned}\sqrt{m}+1&=\sqrt{m+9} \\ \sqrt{\color{red}{16}}\color{black}{+}1& \stackrel{?}{=} \sqrt{\color{red}{16}\color{black}{+}9} \\ 4+1& \stackrel{?}{=} 5 \\ 5&=5\end{aligned}\)
The solution is \(m=16\).
Solve \(3-\sqrt{x}=\sqrt{x-3}\).
- Answer
-
\(x=4\)
Solve \(\sqrt{x}+2=\sqrt{x+16}\).
- Answer
-
\(x=9\)
We summarize the steps here. We have adjusted our previous steps to include more than one radical in the equation This procedure will now work for any radical equations.
- Isolate one of the radical terms on one side of the equation.
- Raise both sides of the equation to the power of the index.
- Are there any more radicals?
If yes, repeat Step 1 and Step 2 again.
If no, solve the new equation. - Check the answer in the original equation.
Be careful as you square binomials in the next example. Remember the pattern in \((a+b)^{2}=a^{2}+2 a b+b^{2}\) or \((a-b)^{2}=a^{2}-2 a b+b^{2}\).
Solve \(\sqrt{q-2}+3=\sqrt{4 q+1}\).
Solution
Solve \(\sqrt{x-1}+2=\sqrt{2 x+6}\).
- Answer
-
\(x=5\)
Solve \(\sqrt{x}+2=\sqrt{3 x+4}\).
- Answer
-
\(x=0 x=4\)
Use Radicals in Applications
As you progress through your college courses, you’ll encounter formulas that include radicals in many disciplines. We will modify our Problem Solving Strategy for Geometry Applications slightly to give us a plan for solving applications with formulas from any discipline.
- Read the problem and make sure all the words and ideas are understood. When appropriate, draw a figure and label it with the given information.
- Identify what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
One application of radicals has to do with the effect of gravity on falling objects. The formula allows us to determine how long it will take a fallen object to hit the gound.
On Earth, if an object is dropped from a height of \(h\) feet, the time in seconds it will take to reach the ground is
\(\dfrac{\sqrt{h}}{4}.\)
For example, if an object is dropped from a height of \(64\) feet, we can find the time it takes to reach the ground by substituting \(h=64\) into the formula.
| \(h=64\) and so the time we seek satisfies | \(t=\dfrac{\sqrt{64}}{4}\) |
| Take the square root of \(64\). | \(t=\dfrac{8}{4}\) |
| Simplify the fraction. | \(t=2\) |
It would take \(2\) seconds for an object dropped from a height of \(64\) feet to reach the ground.
Marissa dropped her sunglasses from a bridge \(400\) feet above a river. The time it takes for an object to hit the ground is \(\dfrac{\sqrt{h}}{4}\) seconds. Find how many seconds it took for the sunglasses to reach the river.
- Solution
-
Read the problem. Identify what we are looking. The time it takes for the sunglasses to reach the river. Name what we are looking. Let \(t\) be the time we are looking for. Translate into an equation by equating two different expressions for the same quantity. \(t=\dfrac{\sqrt{400}}{4}\) Solve the equation. \(t=\dfrac{20}{4}\) \(t=5\) Check the answer in the problem and make sure it makes sense. Here, it will solve the original problem, but we must see that it makes sense in the particular application.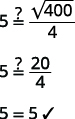 
Does \(5\) seconds seem like a reasonable length of time? Yes. Answer the equation. It will take \(5\) seconds for the sunglasses to reach the river.
A helicopter dropped a rescue package from a height of \(1,296\) feet. The time it takes for it to hit the ground is \(\dfrac{\sqrt{h}}{4}\) seconds. Find how many seconds it took for the package to reach the ground.
- Answer
-
\(9\) seconds
A window washer dropped a squeegee from a platform \(196\) feet above the sidewalk. The time it takes for it to hit the ground is \(\dfrac{\sqrt{h}}{4}\) seconds. Find how many seconds it took for the squeegee to reach the sidewalk.
- Answer
-
\(3.5\) seconds
Police officers investigating car accidents measure the length of the skid marks on the pavement. Then they use square roots to determine the speed, in miles per hour, a car was going before applying the brakes.
If the length of the skid marks (on a certain surface) is \(d\) feet, then the speed of the car before the brakes were applied is
\(\sqrt{24 d} \) miles per hour.
After a car accident, the skid marks for one car measured \(190\) feet. The speed of the car before the brakes were applied is \(\sqrt{24d}\) feet/second. Find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.
- Solution
-
Read the problem. Identify what we are looking for. The speed of a car. Name what we are looking for. Let \(s=\) the speed. Translate into an equation by writing the appropriate formula. Substitute in the given information.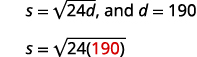 
Solve the equation.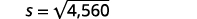 
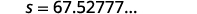
Round to \(1\) decimal place. 
The speed of the car before the brakes were applied was \(67.5\) miles per hour.
An accident investigator measured the skid marks of the car. The length of the skid marks was \(76\) feet. The speed of the car before the brakes were applied is \(\sqrt{24d}\) feet/second. Find the speed of the car before the brakes were applied. Round your answer to the nearest tenth.
- Answer
-
\(42.7\) miles/hour
The skid marks of a vehicle involved in an accident were \(122\) feet long. The speed of the car before the brakes were applied is \(\sqrt{24d}\) feet/second. Find the speed of the vehicle before the brakes were applied. Round your answer to the nearest tenth.
- Answer
-
\(54.1\) miles/hour
- When we are trying to solve a radical equation, what are we trying to accomplish?
- Why do we isolate the term with the radical?
- Is it necessary to check our answers even if we know we did not make a mistake? Give an example to support your answer.
Solve \(2\sqrt{p-3}-3=-p\).
Key Concepts
- Binomial Squares
\(\begin{array}{l}{(a+b)^{2}=a^{2}+2 a b+b^{2}} \\ {(a-b)^{2}=a^{2}-2 a b+b^{2}}\end{array}\) - Solve a Radical Equation
- Isolate one of the radical terms on one side of the equation.
- Raise both sides of the equation to the power of the index.
- Are there any more radicals?
If yes, repeat Step 1 and Step 2 again.
If no, solve the new equation. - Check the answer in the original equation.
- Problem Solving Strategy for Applications with Formulas
- Read the problem and make sure all the words and ideas are understood. When appropriate, draw a figure and label it with the given information.
- Identify what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Falling Objects
- On Earth, if an object is dropped from a height of \(h\) feet, the time in seconds it will take to reach the ground is found by using the formula \(t=\dfrac{\sqrt{h}}{4}\).
- Skid Marks and Speed of a Car
- If the length of the skid marks is \(d\) feet, then the speed of the car before the brakes were applied (on a certain surface) is \(\sqrt{24d}\) miles per hour.
Glossary
- radical equation
- An equation in which a variable is in the radicand of a radical expression is called a radical equation.