3.2.3: Graphs of Certain Quadratic Equations: Part II

Last updated
Save as PDF

Page ID: 100583

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

By the end of this section, you will be able to:

Graph certain quadratic equations with two variables using the idea of intercepts.
Use the intercepts of certain quadratic equations with two variables to find other features of the solutions.

Be Prepared

Before you get started, take this readiness quiz.

Solve $(x-2)(3x-7)=0$.
Find the midpoint of $(3,0)$ and $(7,0)$.
Find a solution of $y=-5x-1$ of the form $(-2,\cdot)$.

Parabolas are somewhat easier to recognize. So we will devote some time here to an alternative strategy.

This involves finding intercepts and making note of the symmetries that we have already recognized. This strategy doesn't always work, but nonetheless can be helpful.

Consider the parabola $y=4x^2-x-6$. We could follow the ideas from the last section. But, we could also take an approach that used the fact that we have an idea of what the parabola looks like already. It opens upward.

Let's start by finding some special points:

The $y$-intercept (where the graph crosses the $y$-axis) has the form $(0,b)$. So, we can find $b$ be substituting this into the equation to find $b=-6$.

The $x$-intercept(s) (where the graph crosses the $x$-axis) has the form $(a,0)$. So we need to solve $0=4a^2-a-6$, which we will use the quadratic formula for. We arrive at two intercepts: $\left(\dfrac{1}{8}+\dfrac{\sqrt{97}}{8},0\right)$ and $\left(\dfrac18-\dfrac{\sqrt{97}}{8},0\right)$.

Note that the formula gives us two solutions: $\dfrac{1}{8}+$ something and $\dfrac{1}{8}-$ the same something. The average of these two is $\dfrac{1}{8}$ which is the $x$-coordinate of the vertex!! To find the $y$-coordinate we need to find a solution of the equation of the form $\left(\dfrac18,b\right)$ which turns out to give $\left(\dfrac18,\dfrac{-97}{16}\right)$ as the vertex.

Using symmetry of the parabola we can form the sketch which we provide with Desmos:

$desmos-graph (22).png$

This idea is especially nice if you can put it in a particular form where the intercepts are easy to find.

Example $\PageIndex{1}$

1. Sketch the graph of $y=(x-2)(x+1)$.

2. Write an equation for the following graph

$desmos-graph (24).png$

Solution

1. Here the $y$-intercept is $(0,-2)$ and the $x$-intercept(s), being of the form $(a,0)$, are $(2,0)$ and $(-1,0)$.

The $x$-coordinate of the vertex is midway between the $x$-intercepts which is $\dfrac{2+-1}{2}=\dfrac12$. So the vertex is at $\left(\dfrac12,-\dfrac94\right)$. We graph this information and complete the sketch.

$desmos-graph (23).png$

2. The parabola opens downward and has $x$-intercepts $(-2,0)$ and $(-3,0)$. It follows that the parabola has the form $ay=(x+2)(x+3)$. We can find $a$ by noting that $\left(-\dfrac52,1\right)$ is on the graph and should therefore satisfy the equation. This gives us that $a=-\dfrac14$. So our equation is $-\dfrac{y}{4}=(x+2)(x+3)$. This can be checked on Desmos.

Exercise $\PageIndex{1}$

1. Sketch the graph of $x=(y+2)(y-1)$.

2. Write an equation for the following graph

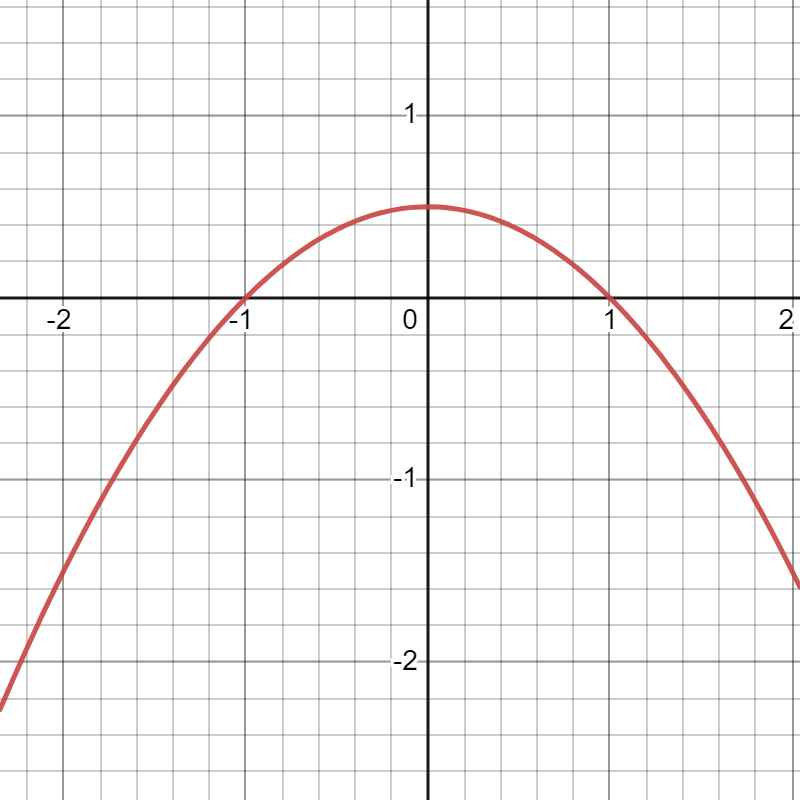$desmos-graph (25).png$

Answer

1. Check your answer on Desmos.

2. $-2y=(x+1)(x-1)$.

These ideas are helpful, but sometimes not sufficient. For example maybe there are no $x$-intercepts. In which case, the vertex is still 'in between' as if there were. Or, in the case of an upward opening parabola, for example, the vertex coincides with the $x$-intercepts, and therefore also with the vertex. You may in these and similar cases plot some points to help.

Key Concepts

When sketching a parabola, depending on its form, you may want to do the following to guide your sketch:

Find the intercepts
Locate the vertex (note the symmetry of the parabola)

Learning Objectives

Be Prepared

Example \(\PageIndex{1}\)

Exercise \(\PageIndex{1}\)

Key Concepts