4.1.1: Angles and Triangles
- Page ID
- 94198
By the end of this section, you will be able to:
- Communicate about triangles.
- Know what it means for two triangles to be similar.
- Know what a right triangle is and what relationship its sides have.
- Determine the measure of a missing interior angle of a triangle if the other two are known.
Before you get started, take this readiness quiz.
- Solve \(x+40=18\).
- Reduce \(\dfrac{90}{2}\).
In elementary geometry, angles are always considered to be positive and not larger than \(360°\). You also learned that the sum of the angles in a triangle equals \(180°,\) and that an isosceles triangle is a triangle with two sides of equal length. Recall that in a right triangle one of the angles is a right angle. Thus, in a right triangle one of the angles is \(90°\) and the other two angles are acute angles whose sum is \(90°\) (i.e. the other two angles are complementary angles).
Angles are what is formed when two rays, lines or line segments come together. Here are two examples:
In the above the angle on the right seems 'bigger' than the angle on the left. In order to quantify this observation, we first clarify some vocabulary.
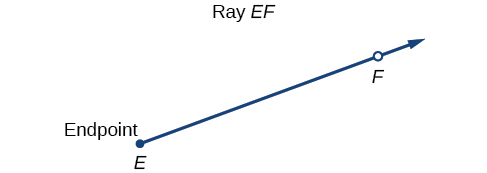
Properly defining an angle first requires that we define a ray. A ray consists of one point on a line and all points extending in one direction from that point. The first point is called the endpoint of the ray. We can refer to a specific ray by stating its endpoint and any other point on it. The ray in Figure \(\PageIndex{1}\) can be named as ray EF, or in symbol form \(\overrightarrow{EF}\).
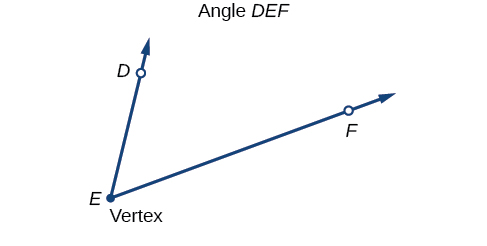
An angle is the union of two rays having a common endpoint. The endpoint is called the vertex of the angle, and the two rays are the sides of the angle. The angle in Figure \(\PageIndex{2}\) is formed from \(\overrightarrow{ED}\) and \(\overrightarrow{EF}\). Angles can be named using a point on each ray and the vertex, such as angle DEF, or in symbol form \(\angle DEF\) or, if no confusion will arise, it can be labeled by the vertex alone (\(\angle E)\) or some other letter that may be indicated on the picture.
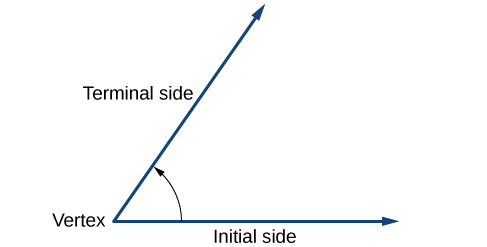
We can think of angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side, and the rotated ray is the terminal side. In order to identify the different sides, we indicate the rotation with a small arc and arrow close to the vertex as in Figure \(\PageIndex{3}\).
Here are some examples with the angles indicated by an arc.
.png?revision=2&size=bestfit&width=238&height=246)
To quantify the comparison at the beginning of this section, we must be able to measure them.
The measure of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. To begin we agree that the measure of an angle formed when the two segments are identical forms a 360 degree angle.
So, one degree is \(\dfrac{1}{360}\) of a circular rotation. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol \(^{\text{o}}\). For example, \(90 \text{ degrees } = 90^{\text{o}}\).
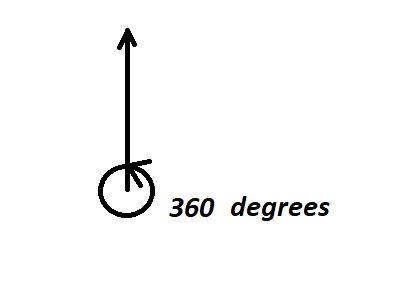
.png?revision=2&size=bestfit&width=266&height=222)
Half of that angle is then \(180^{\text{o}}\). This is called a straight angle:
_180.png?revision=1&size=bestfit&width=300&height=142)
Half of a straight angle has a measure of \(90^{\text{o}}\) and is called a right angle:
.png?revision=1&size=bestfit&width=460&height=225)
Half of a right angle has a measure of \(45^{\text{o}}\):
.png?revision=1&size=bestfit&width=214&height=221)
And so on. There is an instrument, called a protractor that helps us to measure angles that are drawn on paper.
When three line segments are drawn in a way that encloses an area we have what is called a triangle. There are six angles formed by the sides of a triangle, three are outside and three are inside the triangle. We could, if we had an accurate picture of a triangle, measure these angles with a protractor. If we measured the interior angles and added them up, we would discover a remarkable fact that the sum is \(180°\). We should at this point, draw some triangles and measure them to check this out. We show a picture giving an idea of why this is true here:
.png?revision=1&size=bestfit&width=512&height=430)
For any triangle, there are 3 side lengths and 3 (interior) angle measurements. We say that an angle is adjacent to a side (or the side is adjacent to the angle) if the side is one of the two forming the angle. We say that an angle is opposite a side (or the side is opposite the angle) if the side is not adjacent to the angle.
.png?revision=1&size=bestfit&width=528&height=308)
The sides and angles are sometimes labeled with variables representing their measure. Often (but not always) the the variable representing the measure of an angle is a greek letter (usually \(\theta\) or \(\psi\)).
An angle is acute if it is between \(0°\) and \(90°\) and is obtuse if it is between \(90°\) and \(180°\).

In elementary geometry, angles are always considered to be positive and not larger than \(360° \). For now we will only consider such angles. The following definitions are also sometimes used when discussing angles.
It is often the case that the name of the angle is used as the value. For example, if we call the angle \(\angle A\) and the measure of angle \(\angle A\) is \(45\) degrees (notated \(45°\)) then we may also say \(\angle A=45°\).
- Two acute angles are complementary if their sum equals \(90°\). In other words, if \(0° ≤ \angle A , \angle B ≤ 90° \text{ then }\angle A \text{ and }\angle B\) are complementary if \(\angle A +\angle B = 90°\).
- Two angles between \(0°\text{ and }180°\) are supplementary if their sum equals \(180°\). In other words, if \(0° ≤ \angle A , \angle B ≤ 180° \text{ then }\angle A \text{ and }\angle B\) are supplementary if \(\angle A +\angle B = 180°\).
- Two angles between \(0°\text{ and }360°\) are conjugate if their sum equals \(360°\). In other words, if \(0° ≤ \angle A , \angle B ≤ 360° \text{ then }\angle A \text{ and }\angle B\text{ are conjugate if }\angle A+\angle B = 360°\).
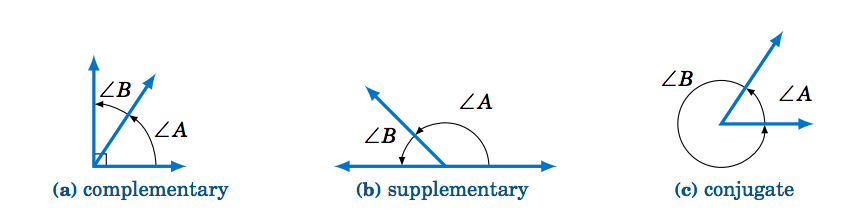
Sometimes the measure of angles are named by the vertex or they may be given variable names like \(x, y,\) or \(z\). Often they are given names from the greek alphabet, most commonly \(\theta, \phi, \psi, \alpha,\beta,\) or \(\gamma\) (theta, phi, alpha, beta, or gamma, respectively).
Triangles
When three line segments are drawn in a way that encloses an area we have what is called a triangle. There are six angles formed by the sides of a triangle, three are outside and three are inside the triangle. We could, if we had an accurate picture of a triangle, measure these angles with a protractor. If we measured the interior angles and added them up, we would discover a remarkable fact that the sum is \(180^{\text{o}}\). We should at this point, draw some triangles and measure them to check this out. We show a picture giving an idea of why this is true here:
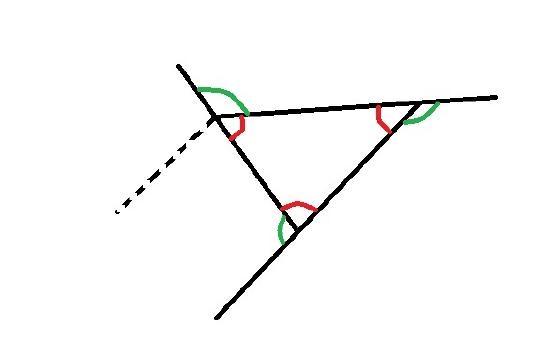
The sum of the green angles (outside) is \(360°\) (noting corresponding angles with the rays parallel to the dotted ray) and the sum of each of the red green pairs is \(180°\). So, the sum of all of the red green pairs is \(3(180)°\) which is the same as the sum of the red angles plus the sum of the green angles (\(360°\)). It follows that the sum of the red angles is \((3(180)-360)°=180°\).
For any triangle, there are 3 side lengths (here, \(a,b\), and \(c\)) and 3 angle measurements (here \(A,B,\) and \(C \)):
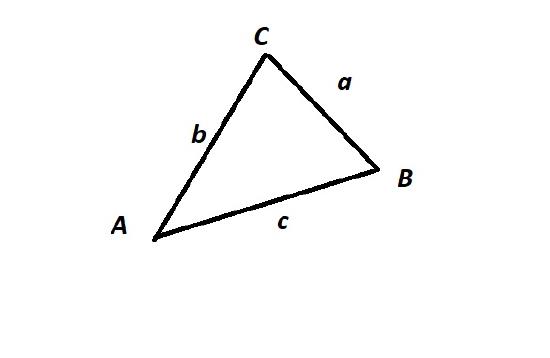
Recall that we will sometimes identify the measure of an angle with the angle itself. We will do the same with sides. For example, we may refer to side \(b\) when \(b\) is the length of the side to which we refer. So, in the diagram above, for example we may refer to the angle \(A\) as well as assign a value to \(A\) which is the measure of that angle and we may refer to the side \(a\) as well as the length of that side as \(a\).
We say that an angle is adjacent to a side (or the side is adjacent to the
angle) if the side is one of the two forming the angle.
For, example,
- side \(b\) is adjacent to angle \(A\) and adjacent to angle \(C\)
- angle \(B\) is adjacent to side \(a\) and adjacent to side \(c\)
We say that an angle is opposite a side (or the side is opposite the angle) if the
side is not adjacent to the angle.
In the above picture, we can say, for example,
- side \(a\) is opposite angle \(A\)
- angle \(B\) is opposite side \(b\)
- side \(c\) is opposite angle \(C\).
Recall the following definitions from elementary geometry:
An isosceles triangle is a triangle with two sides of equal length and a right triangle is a triangle where one of the angles is a right angle. Because the sum of the interior angles of a triangle equals \(180°\), in a right triangle one of the angles is \(90°\) and the other two angles are acute angles whose sum is \(90°\) (i.e. the other two angles are complementary angles). We can use our knowledge of solving equations to discover measures of angles if enough information is known.
For each triangle below, determine the unknown angle(s):

Note: We will sometimes refer to the angles of a triangle by their vertex points. For example, in the first triangle above we will simply refer to the angle \(\angle\,BAC\) as angle \(A\).
Solution:
For triangle \(\triangle\,ABC\), \( A = 35°\) and \(C = 20°\), and we know that \(A + B + C = 180°\), so
\[\nonumber 35° + B + 20° = 180° ⇒ B = 180° − 35° − 20° ⇒ \fbox{\(B = 125°\)} . \nonumber \]
For the right triangle \(△DEF,\, E = 53° \text{ and }F = 90°\), and we know that the two acute angles \(D\) and \(E\) are complementary, so
\[\nonumber D + E = 90° ⇒ D = 90° − 53° ⇒ \fbox{\(D = 37°\)} . \nonumber \]
For triangle \(△ XY Z\), the angles are in terms of an unknown number \(α\), but we do know that \(X +Y + Z = 180°\), which we can use to solve for \(α\) and then use that to solve for \(X, Y, \text{ and }Z\):
\[\nonumber α + 3α + α = 180° ⇒ 5α = 180° ⇒ α = 36° ⇒ \fbox{\(X = 36° ,\, Y = 3×36° = 108° ,\, Z = 36°\)} \nonumber \]
If \(\triangle\,ABC\) has \(A = 25°\) and \(B = 15°\), then what is the measure of angle \(C\)?
- Answer
-
\(C=140°\)
If \(\triangle\,ABC\) has \( B = 125°\) and \(C = 10°\), then what is the measure of angle \(A\)?
- Answer
-
Add texts here. \(A=65°\).
Thales' Theorem states that if \(A, \, B,\text{ and }C\) are (distinct) points on a circle such that the line segment \(\overline{AB}\) is a diameter of the circle, then the angle \(\angle\,ACB\) is a right angle (see Figure 1.1.3(a)). In other words, the triangle \(\triangle\,ABC\) is a right triangle.
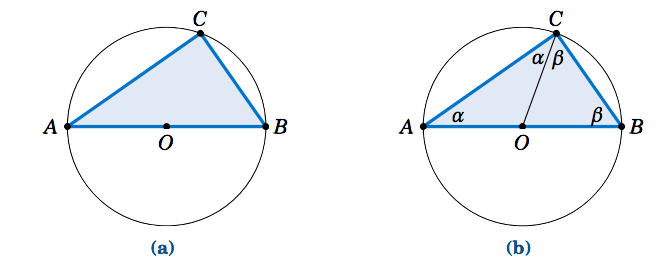
To prove this, let \(O\) be the center of the circle and draw the line segment \(\overline{OC}\), as in Figure 1.1.3(b). Let \(α = \angle BAC \text{ and }β = ∠ ABC\). Since \(\overline{AB}\) is a diameter of the circle, \(\overline{OA} \text{ and }\overline{OC}\) have the same length (namely, the circle’s radius). This means that \(△OAC \text{ is an isosceles triangle, and so }∠OCA = ∠OAC = α\). Likewise, \(△OBC\) is an isosceles triangle and \(∠OCB = ∠OBC = β\). So we see that \(∠ ACB = α+β\). And since the angles of \(△ ABC\) must add up to \(180°\), we see that \(180° = α+(α+β)+β = 2 (α+β), \text{ so }α+β = 90°\). Thus, \(∠ ACB = 90°\).
Similar Triangles
Similar triangles are triangles that have the same shape, i.e., the same angles. Two angles of two similar triangles (one angle from each triangle) are called corresponding if they have the same measure, and sides opposite corresponding angles are called corresponding sides. Ratios of corresponding sides is the same for each pair as seen in the figure below. In the figure, the sides are labeled (order is unimportant) by listing the names of the two points that define the side and to avoid clutter in the ratios, the bar indicating the segment is dropped.
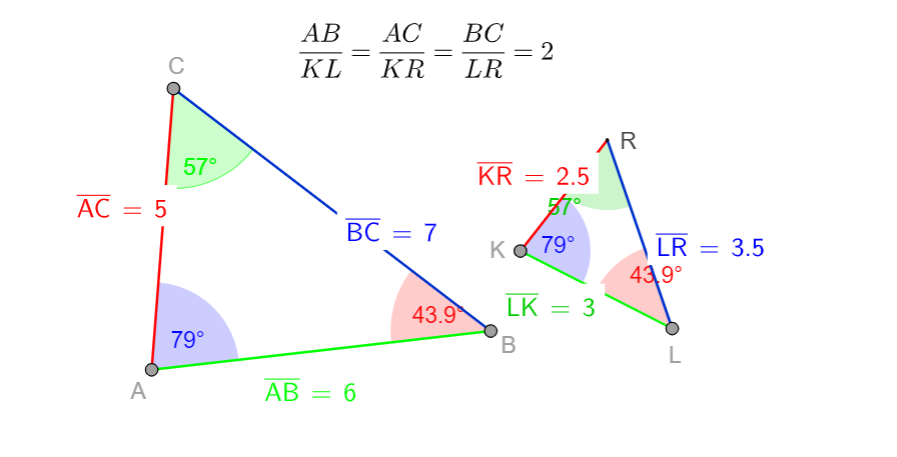
See https://www.geogebra.org/m/z9NHEdrz for the interactive version of the figure above. In this instance, notice that the side opposite the \(57°\) angle is \(6\) on the larger and \(3\) on the smaller. The larger length is twice the smaller length. The same is true of the other lengths. This is confirmed by the ratio calculation the triangles.
Looking at the first equality above we also see that \(\dfrac{\overline{KL}}{\overline{KR}}=\dfrac{\overline{AB}}{\overline{AC}}\) since \(\dfrac{2.5}{3}=\dfrac{2.5\cdot 2}{3\cdot 2}=\dfrac{5}{6}\) (the factor of increase of lengths cancels in the fraction).
So, the ratios of lengths remain the same if the size is changed.
Right Triangles
While we have used what is known as the Pythagorean Theorem, or Pythagoras' Theorem, in this section we provide a proof. We recall that a right triangle is one with a \(90°\) angle. We can conclude that the sum of the measure of the other two angles is \(90°\). Like the angles, the sides of a right triangle are also related so that knowing the length of two sides leads to discovery of the length of the third side. Unlike the angle case where we encountered linear equations, here we will encounter a quadratic equation by using the Pythagorean Theorem:
The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of its legs. So if the triangle is labeled in the following way, we have \(c^2=a^2+b^2\):
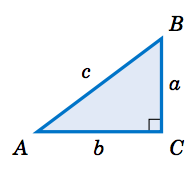
Here is one way to see this. Create a fourth segment so that we have three triangles and label them as shown.
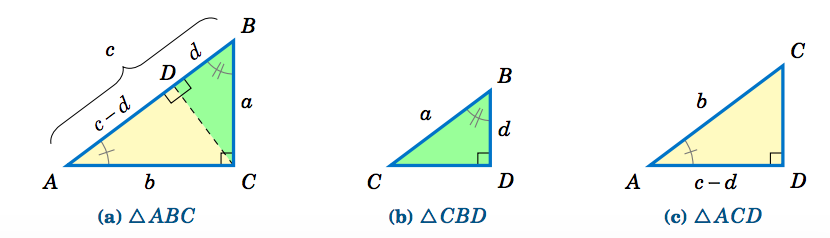
Two triangles are similar if their corresponding angles are equal, and that similarity implies that corresponding sides are proportional. Thus, since \(\triangle\,ABC \) is similar to \(\triangle\,CBD \), by proportionality of corresponding sides we see that
\[\nonumber \overline{AB}~\text{is to}~\overline{CB}~\text{(hypotenuses)}\text{ as }
\overline{BC}~\text{is to}~\overline{BD}~\text{(vertical legs)}
\quad\Rightarrow\quad \dfrac{c}{a} ~=~ \dfrac{a}{d} \quad\Rightarrow\quad cd ~=~ a^2 ~. \nonumber \]
Since \(\triangle\,ABC \) is similar to \(\triangle\,ACD \), comparing horizontal legs and hypotenuses gives
\[\nonumber \dfrac{b}{c-d} ~=~ \dfrac{c}{b} \quad\Rightarrow\quad b^2 ~=~ c^2 ~-~ cd ~=~ c ^2 ~-~ a^2
\quad\Rightarrow\quad a^2 ~+~ b^2 ~=~ c^2 ~. \textbf{QED} \nonumber \]
Note: The symbols \(\perp\) and \(\sim\) denote perpendicularity and similarity, respectively. For example, in the above proof we had \(\,\overline{CD} \perp \overline{AB}\, \) and \(\,\triangle\,ABC \sim \triangle\,CBD \sim \triangle\,ACD \).
For each right triangle below, determine the length of the unknown side:
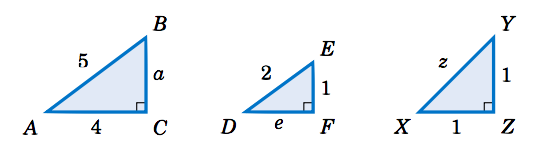
Solution:
For triangle \(\triangle\,ABC \), the Pythagorean Theorem says that
\[\nonumber a^2 ~+~ 4^2 ~=~ 5^2 \quad\Rightarrow\quad a^2 ~=~ 25 ~-~ 16 ~=~ 9 \quad\Rightarrow\quad
\fbox{\(a ~=~ 3\)} ~. \nonumber \]
For triangle \(\triangle\,DEF \), the Pythagorean Theorem says that
\[\nonumber e^2 ~+~ 1^2 ~=~ 2^2 \quad\Rightarrow\quad e^2 ~=~ 4 ~-~ 1 ~=~ 3 \quad\Rightarrow\quad
\fbox{$e ~=~ \sqrt{3}$} ~. \nonumber \]
For triangle \(\triangle\,XYZ \), the Pythagorean Theorem says that
\[\nonumber 1^2 ~+~ 1^2 ~=~ z^2 \quad\Rightarrow\quad z^2 ~=~ 2 \quad\Rightarrow\quad
\fbox{$z ~=~ \sqrt{2}$} ~. \nonumber \]
If \(\triangle\,ABC\) has \( C = 90°\), \(b = 10\text{ in }\) and \(c=15\text{ in }\), then what is the length of \(a\)?
- Answer
-
\(a=5\sqrt{5}\text{ in }\)
If \(\triangle\,ABC\) has \( a = 12\), \(b= 10\), and \(c=4\) (all measured in the same unit), then is \(\triangle \,ABC\) a right triangle?
- Answer
-
No, it can not be a right triangle.
A 17 ft ladder leaning against a wall has its foot 8 ft from the base of the wall. At what height is the top of the ladder touching the wall?
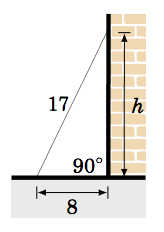
Solution
Let \(h\) be the height at which the ladder touches the wall. We can assume that the ground makes a right angle with the wall, as in the picture on the right. Then we see that the ladder, ground, and wall form a right triangle with a hypotenuse of length 17 ft (the length of the ladder) and legs with lengths 8 ft and \(h\) ft. So by the Pythagorean Theorem, we have
\[\nonumber h^2 + 8^2 = 17^2 \quad\Rightarrow\quad h^2 = 289 - 64=225 \quad\Rightarrow\quad
\fbox{$h = 15 \text{ ft}$} ~. \nonumber \]
You and your friend are talking at a street corner and upon parting, you walk north at \(2\) mph and your friend walks east at \(3\) mph. You have a walkie talkie system that you are using that has a range of 5 miles. Approximately, how long will you be able to continue talking? Explain reasoning clearly.
- Answer
-
Answers vary. About 83 minutes.
How long of a ladder do you need if you need to reach a light attached to a wall 10 feet from the ground if for stability's sake you need the base of the ladder to be 2.5 feet from the base of the wall? Be sure to draw a picture that represents the situation.
- Answer
-
The ladder should be \(\dfrac{5\sqrt{17}}{2}\) feet (about 10.3 feet) . Here we have assumed the ladder meets the wall 10 feet above the ground.
- How can you recognize if two triangles are similar?
- Do you know of examples in your life where similar triangles (or similar objects) appear?
- Construct a triangle which is not a right triangle and show that the Pythagorean Theorem is not true.
- Give an example of an acute angle and its complement. Draw a picture showing the relationship.
1. If two of the three interior angles of a triangle are 40 degrees, what is the third angle? Draw a picture of the situation. Are all triangles that you could draw similar to one another?
2. If the legs of a right triangle measure \(7\text{ in}\) and \(9\text{ in}\), how long is the hypotenuse? Draw a picture of this situation.
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- A right angle is \(\dfrac14\) of a complete revolution.
- A triangle is a made by connecting 3 points (vertices) pairwise by line segments.
- A right triangle is a triangle with one of the interior angles being a right angle.
- Interior angles of a triangle add up to \(180°\).
- Two triangles are similar if they are the same shape but not necessarily the same size.
- Two triangles which are similar have equal corresponding ratios of sides.
- Pythagoras' Theorem

