4.1.2: Right Triangles and Trigonometric Ratios

Last updated
Save as PDF

Page ID: 105343

Holly Carley and Ariane Masuda
New York City College of Technology

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Understand what it means for two right triangles to be similar to each other.
Be able to produce two special triangles.
Be able to use ratios to determine missing side lengths of a triangle (with and without (if possible) a calculator).
Be able to find missing angles of a right triangle if the lengths of the sides are known.

Be Prepared

Before you get started, take this readiness quiz.

Solve $\dfrac{2}{x}=\dfrac{3}{5}$.
Solve $\dfrac{x}{4}=\dfrac{4}{5}$.
Draw a picture of a right triangle and identify its hypotenuse.

Similar Triangles and Trigonometric Ratios

A right triangle is a triangle with one of the angles being $90^{\text{o}}$. This is a special angle and the side opposite is called the hypotenuse. There are two other angles which are not distinguished but we may name them or assign a variable to represent their measure.

So if we label one of the two right angles with its measure $\theta$ then of the two undistinguished sides (not the hypotenuse) there is one that is opposite and one that is adjacent.
$geogebra-export (15).png$

Two right triangles are similar if one (and therefore both) of the non-right interior angles are equal! So, for example, all right triangles with an interior angle of $40^{\text{o}}$ are similar to each other. Recall that if two triangles are similar, the corresponding ratios are equal. We consider such ratios (determined only by the shape/interior angles) for a right triangle.

There are 6 ratios that we can consider (three are reciprocals of the other three). We would like to name these and to do this we will label an angle $\theta$ representing
its measure. Then the three sides now have names: hypotenuse, opposite, and adjacent. The six ratios are opposite/hypotenuse, adjacent/hypotenuse, and opposite/adjacent together with their reciprocals.

The names though are with reference to one of the angles. We then call these ratios:

$\sin\theta= \dfrac{\text{opposite}}{\text{hypotenuse}}$ (read 'sine of theta')
$\cos\theta=\dfrac{\text{adjacent}}{\text{hypotenuse}}$ (read 'cosine of theta')
$\tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}$ (read 'tangent of theta')

and their corresponding reciprocals:

$\csc\theta=\dfrac{1}{\sin\theta}$ (read 'cosecant of theta')
$\sec\theta=\dfrac{1}{\cos\theta}$ (read 'secant of theta')
$\cot\theta=\dfrac{1}{\tan\theta}$ (read 'cotangent of theta')

Notice that if we had used the other non-right angle as our reference angle instead our ratios would be formed the same way but adjacent and opposite are
switched and so the names would change accordingly (putting a co- or removing a co-):

$geogebra-export (16).png$

$\sin\theta=\cos\psi,\cos\theta=\sin\psi,\tan\theta=\cot\psi, \dots$ etc

So, for instance, when seeing the expression $\sin \theta$ we understand the reference angle is the one with measure $\theta$ and the ratio is the length of the side opposite that angle divided by the length of the hypotenuse. The word 'sin' makes no sense by itself because it lacks a reference angle. Sometimes parentheses are present and sometimes we may write $\sin \theta$ as $\sin \theta$ and should not be confused with multiplication.

In all of the examples and figures, we should not treat the figures as anything but representing relationships. So, for example, you should not think that measuring with any instrument will lead to a solution. We have also not written units.

Example $\PageIndex{1}$

Given the figure below, relate $\theta$ to the given numbers using one of the three ratios ($\sin\theta,\cos\theta,\tan\theta$). Then find the other 5 ratios with reference angle $\theta$.

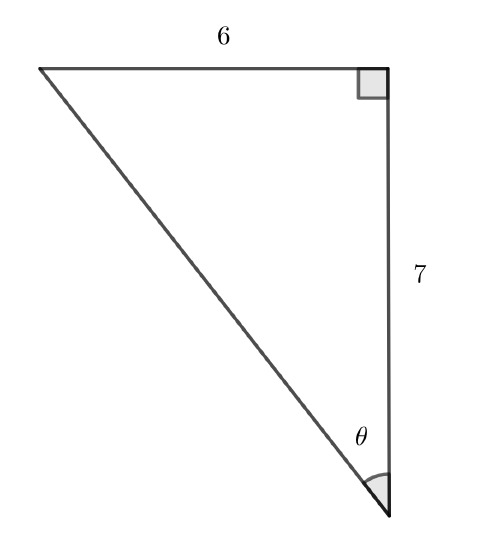
$example ratio question.png$

Solution

We first identify the where the measured sides are as it relates to the marked angle.

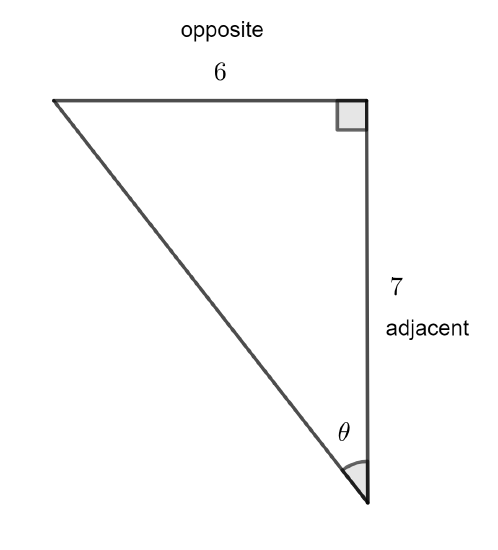
$example ratio 2.png$

Now we look at the ratios:

$\sin\theta= \dfrac{\text{opposite}}{\text{hypotenuse}}$ (read 'sine of theta')
$\cos\theta=\dfrac{\text{adjacent}}{\text{hypotenuse}}$ (read 'cosine of theta')
$\tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}$ (read 'tangent of theta')

and see that the one that we could use is $\tan\theta=\dfrac{\text{opposite}}{\text{adjacent}}$. So,

\[\tan\theta=\dfrac67.\nonumber\]

To find the other five ratios we need the length of the hypotenuse. Since this is a right triangle, Pythagoras tells us that the square of the length of the hypotenuse is the sum of the squares of the length of the legs. If we call the length of the hypotenuse $c$, then, in this case,

\[c^2=6^2+7^2=85,\nonumber\]

so that $c=\sqrt{85}$ since the length of the hypotenuse can not be negative.

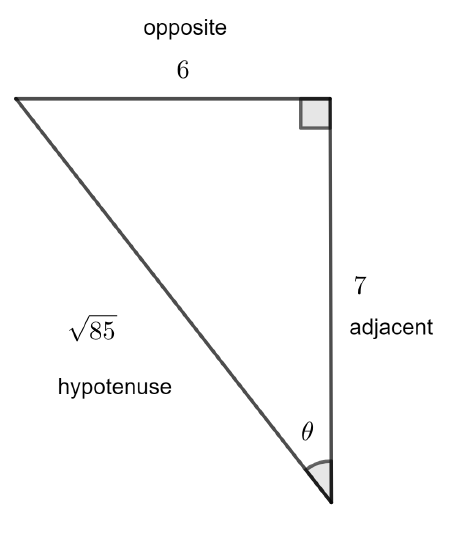
$example ratio.png$

Forming the other ratios gives us

$\sin\theta=\dfrac{6}{\sqrt{85}}$
$\cos\theta=\dfrac{7}{\sqrt{85}}$
$\csc\theta=\dfrac{1}{\sin(\theta)}=\dfrac{\sqrt{85}}{6}$
$\sec\theta=\dfrac{1}{\cos(\theta)}=\dfrac{\sqrt{85}}{7}$
$\cot\theta=\dfrac{1}{\tan(\theta)}=\dfrac76$

Try It $\PageIndex{2}$

Given the figure below, relate $\theta$ to the given numbers using one of the three ratios ($\sin\theta,\cos\theta,\tan\theta)$. Then find the other 5 ratios with reference angle $\theta$.

$exercise ratio question (1).png$

Answer

$\cos\theta=\dfrac{7}{10}$. The unknown leg length is $\sqrt{51}$.

$\sin\theta=\dfrac{\sqrt{51}}{10}$
$\cos\theta=\dfrac{7}{10}$
$\tan\theta=\dfrac{\sqrt{51}}{7}$
$\csc\theta=\dfrac{1}{\sin(\theta)}=\dfrac{10}{\sqrt{51}}$
$\sec\theta=\dfrac{1}{\cos(\theta)}=\dfrac{10}{7}$
$\cot\theta=\dfrac{1}{\tan(\theta)}=\dfrac{7}{\sqrt{51}}$

Try It $\PageIndex{3}$

Given the figure below, relate $\theta$ to the given numbers using one of the three ratios ($\sin\theta,\cos\theta,\tan\theta)$. Then find the other 5 ratios with reference angle $\theta$.

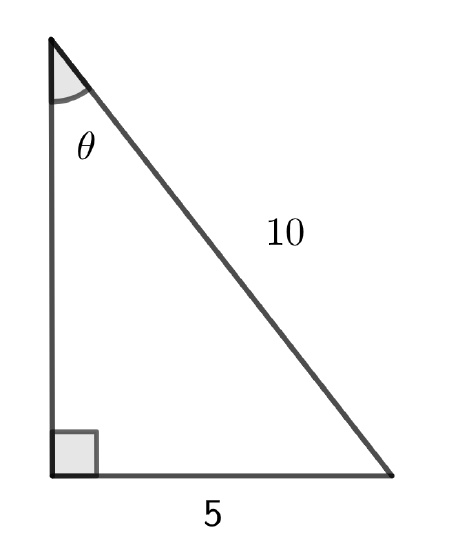
$exercise ratio question 2.png$

Answer

$\sin\theta=\dfrac{5}{10}=\dfrac12$ and the hypotenuse is $\sqrt{75}=5\sqrt{3}$.

$\sin\theta=\dfrac{1}{2}$
$\cos\theta=\dfrac{\sqrt{3}}{2}$
$\tan\theta=\dfrac{\sqrt{1}}{\sqrt{3}}$
$\csc\theta=\dfrac{1}{\sin\theta}=2$
$\sec\theta=\dfrac{1}{\cos\theta}=\dfrac{2}{\sqrt{3}}$
$\cot\theta=\dfrac{1}{\tan\theta}=\sqrt{3}$

Example $\PageIndex{4}$

Suppose you know that for a particular angle of a right triangle, $\theta$, that $\cos\theta=\dfrac59$. Draw a picture that shows the relationship between $\theta$, $5$, and $9$. Find the other ratios.

Solution

We know that the ratio $\cos\theta$ is $\dfrac{\text{adjacent}}{\text{hypotenuse}}$ (relative to the angle with measure $\theta$). Since $\dfrac59$ is a fraction, we will simply use the numerator as the length of the adjacent leg, and the $9$ as the length of the hypotenuse:

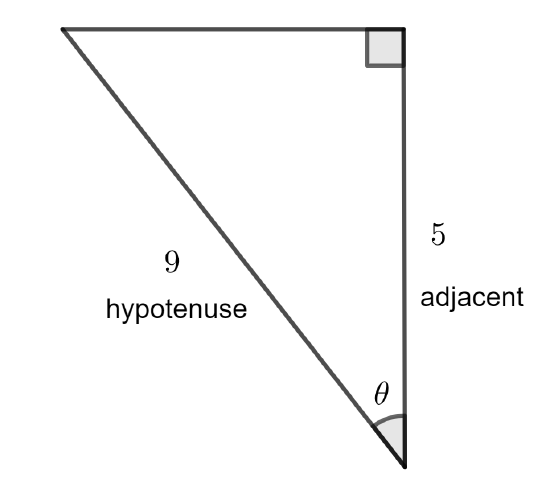
$example ratio question a.png$

There are many pictures you could draw, but most are a little 'unnatural'. For example, we can view $\dfrac59=\dfrac{\dfrac59}{1}$ to give

$example ratio b (1).png$

To find the other ratios we will need the length of the opposite, which we will call $a$. When we write down an equation for $a$ it may be easier to use the first of the two triangles, though the ratios will be the same.

So, using the first triangle we see that $a$ satisfies

\[9^2=a^2+5^2.\nonumber\]

subtracting $5^2$ gives us

\[a^2=9^2-5^2=(9+5)(9-5)=14\cdot 4\nonumber\]

Here we anticipated needing to simplify a square root and took advantage of the difference-of-squares form. We hope, though perhaps in vain, that there will be some simplifications in the ratios.

So,

\[a=2\sqrt{14}.\nonumber\]

$example ratio question a labeled with opp (1).png$

Now we form the remaining ratios:

$\sin\theta=\dfrac{2\sqrt{14}}{9}$
$\tan\theta=\dfrac{2\sqrt{14}}{5}$
$\csc\theta=\dfrac{1}{\sin\theta}=\dfrac{9}{2\sqrt{14}}$
$\sec\theta=\dfrac{1}{\cos\theta}=\dfrac{9}{5}$
$\cot\theta=\dfrac{1}{\tan\theta}=\dfrac{5}{2\sqrt{14}}$

Try It $\PageIndex{5}$

Suppose you know that for a particular angle of a right triangle, $\theta$, that $\tan\theta=3$. Draw a picture that shows the relationship between $\theta$ and $3$. Find the other ratios.

Answer

Triangles vary.

$\sin\theta=\dfrac{3}{\sqrt{10}}$
$\cos\theta=\dfrac{1}{\sqrt{10}}$
$\tan\theta=3$
$\csc\theta=\dfrac{1}{\sin\theta}=\dfrac{\sqrt{10}}{3}$
$\sec\theta=\dfrac{1}{\cos\theta}=\sqrt{10}$
$\cot\theta=\dfrac{1}{\tan\theta}=\dfrac{1}{3}$

Try It $\PageIndex{6}$

Suppose you know that for a particular angle of a right triangle, $\theta$, that $\sin\theta=\dfrac{4}{5}$. Draw a picture that shows the relationship between $\theta$, $4$, and $5$. Find the other ratios.

Answer

Answers vary.

$\sin\theta=\dfrac{4}{5}$
$\cos\theta=\dfrac{3}{5}$
$\tan\theta=\dfrac43$
$\csc\theta=\dfrac{1}{\sin\theta}=\dfrac{5}{4}$
$\sec\theta=\dfrac{1}{\cos\theta}=\dfrac{5}{3}$
$\cot\theta=\dfrac{1}{\tan\theta}=\dfrac{3}{4}$

There are two special triangles that will be important in what follows where the ratios are known exactly (in terms of square roots).

First, consider an isosceles right triangle:

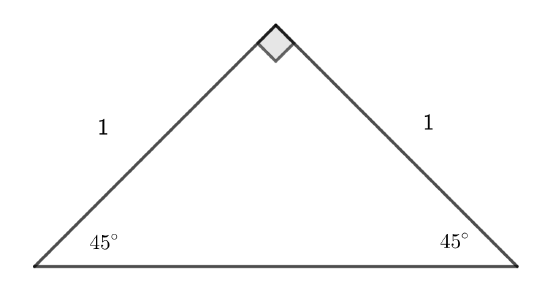
$4545base.png$

We can use the Pythagorean Theorem to find that the hypotenuse is $\sqrt{2}$.

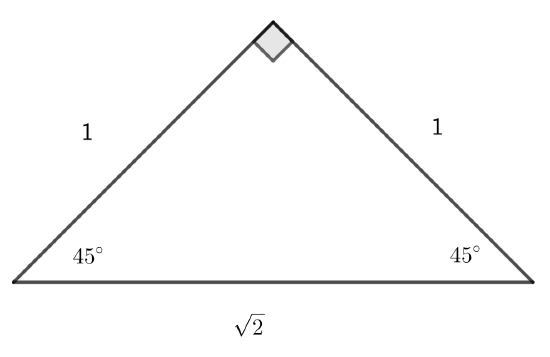
$4545baseplus.png$

So, for example, $\cos{45^\text{o}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$.

For the second special triangle, consider an equilateral triangle.

$equil.png$

In anticipation of simpler arithmetic, we will make all of the sides have length 2 units. Now we form a line that bisects the upper angle thereby forming two smaller triangles. The bottom inner angle must by a right angle. The resulting triangles are the same shape since their angles are the same and they are the same size since the hypotenuse is $2$ for each. So the line bisects the base as well leaving us with:

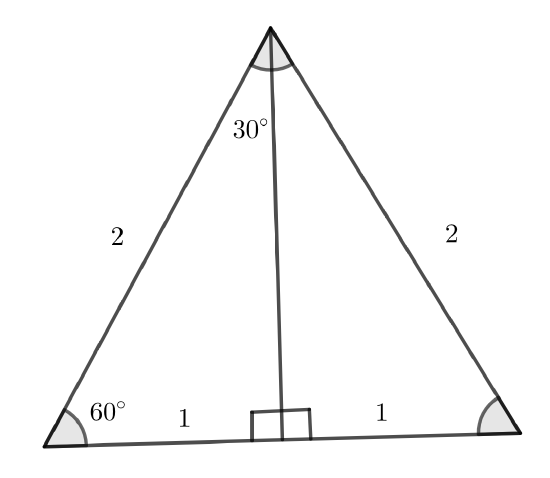
$equil perp.png$

If we focus on the left (extracting it from the picture), we can use the Pythagorean Theorem to find the length of the missing leg (which we can call $a$:

\[2^2=a^2+1^2,\nonumber\]

which leads us to discover that $a=\sqrt{3}$ and so we have the following picture:

$3060fin.png$

You will need to be able to recall (either by memory or re-derivation) these two special triangles often called "the 45-45-90" triangle and "the 30-60-90" triangle. These are just two particular representatives.

$4545baseplus.png$ $3060fin.png$

For the 30-60-90 triangle, it may be helpful to note that opposite the smallest angle is the shortest side, and opposite the largest angle is the longest side.

It follows that, for example, $\tan 60^\text{o}=\sqrt{3}$ etc. It is possibly better to recall the triangle rather than all of ratios.

Example $\PageIndex{7}$

Suppose that I am standing at the tip of a shadow of a building and look at a $60^\text{o}$ angle to the top of a building. The shadow is measured to be 20 feet. Neglecting my height, approximately how tall is the building?

Solution

We first draw a picture and label the information we have:

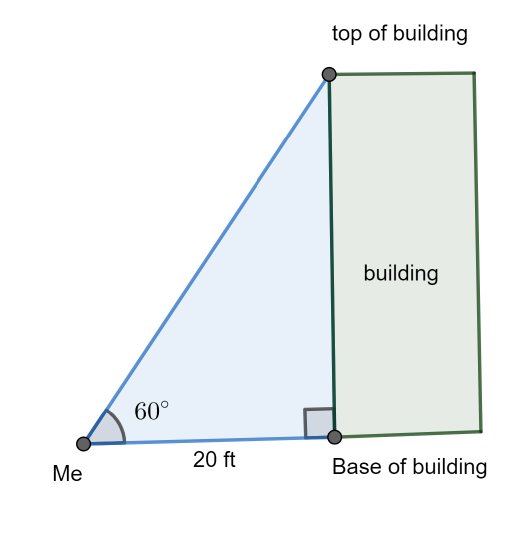
$Example triangles bldg.png$

We want to find the height of the building, so we will call this $h$ and extract just the triangle from the picture. We note that the triangle is a special triangle and we draw by its side the one we know (not to scale) noting that opposite the $30^\text{o}$ angle is $1$.

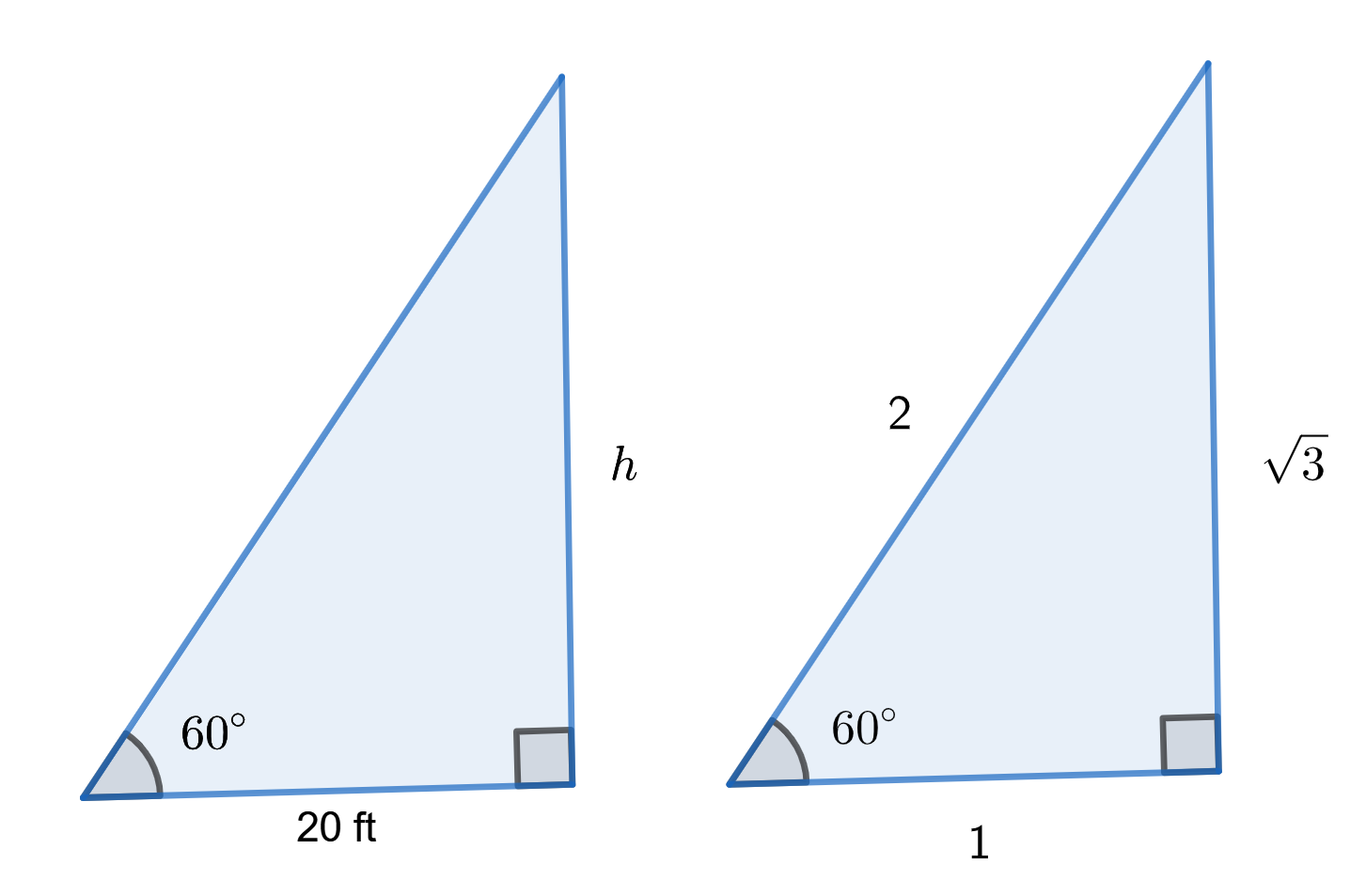
$Example triangles bldg 2.png$

There are two approaches:

The first approach is to use that corresponding ratios are equal:

$\dfrac{h}{20}=\dfrac{\sqrt{3}}{1}$

and then solve for $h$ to get $h=20\sqrt{3}$ . We conclude that the height of the building is approximately 34 feet (because we are neglecting my height that this is only an approximation).

The second approach is to use the ratios:

From the left triangle we see that

$\dfrac{h}{20}=\tan 60^\text{o}$

and the right triangle helps us see that the ratio $\tan 60^\text{o}$ is $\sqrt{3}$. We again find that

$\dfrac{h}{20}=\sqrt{3}$

and proceed as above.

You may find that you prefer one over the other in certain situations.

Note that the angle in the previous example is called the angle of elevation.

Try It $\PageIndex{8}$

Suppose we are looking out a window that is $50$ ft from the ground and we look down at a $45^\text{o}$ angle (this is called the angle of depression) to spot a fire on the ground. Approximately how far away from us in is the fire? Draw a picture of the situation. Why is this only an approximation? Is it a good one?

Answer: Answers vary. The fire is approximately $50\sqrt{2}$ ft from the building.

Try It $\PageIndex{9}$

You are standing in a large field. A drone takes off from your feet at a $30^\text{o}$ angle and runs out of power after traveling $100$ meters. Approximately how far will you have to walk to retrieve the drone? Draw a picture of the situation. Explain why this is an approximation and discuss its accuracy.

Answer: Explanation varies. You will have to walk approximately $50\sqrt{3}$ meters, or $86.6$ m.

Writing Exercise $\PageIndex{10}$

Why must the ratios sine and cosine be less than or equal to one?
Does the tangent ratio have to be less than or equal to one?
In the examples in this section, why doesn't the particular triangle we draw matter as long as it demonstrates the given ratio?
In Example $\PageIndex{7}$, What might the picture look like if I don't neglect my height? Is this a good approximation? We can explore this later.
What is the relationship between $\sin 40°$ and $\cos 50°$? Explain and draw a picture supporting your explanation.

Exit Problem

1. If two right triangles have an interior angle of $30^\text{o}$ give the 6 trigonometric ratios with respect to the $30^\text{o}$ angle.

2. If you are standing a distance of 25 feet from a structure and the angle of elevation to the top of the structure is $45^\text{o}$, how tall is the structure? How far would you have to throw a rock to reach the top? Draw a picture of the situation and support your answer.

Key Concepts

The sides of a right triangle with respect to an angle $\theta$ which is not a right angle are called hypotenuse, opposite, and adjacent according to whether the sides is opposite the right angle, opposite the specified angle, or adjacent (but not the hypotenuse) to the specified angle.
The ratios of the sides of a right triangle are called $\sin\theta=\dfrac{\text{opposite}}{\text{hypotenuse}}$, $\cos\theta=\dfrac{\text{adjacent}}{\text{hypotenuse}}$, and $\tan\theta =\dfrac{\text{opposite}}{\text{adjacent}}$.
There are two families of special triangles: 30-60-90 and 45-45-90 whose ratios are known exactly.

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Solution

Try It \(\PageIndex{2}\)

Try It \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Solution

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Solution

Try It \(\PageIndex{8}\)

Try It \(\PageIndex{9}\)

Writing Exercise \(\PageIndex{10}\)

Exit Problem