4.4: Polynomial Inequalities

Solving Polynomial Inequalities

One application of our ability to find intercepts and sketch a graph of polynomials is the ability to solve polynomial inequalities. It is a very common question to ask when a function will be positive and negative. We can solve polynomial inequalities by either utilizing the graph, or by using test values.

Example 4.4.5

Solve (𝑥 +3)⁢(𝑥+1)2⁢(𝑥 −4) >0

Solution

As with all inequalities, we start by solving the equality (𝑥 +3)⁢(𝑥+1)2⁢(𝑥 −4) =0, which has solutions at x = -3, -1, and 4. We know the function can only change from positive to negative at these values, so these divide the inputs into 4 intervals.

We could choose a test value in each interval and evaluate the function 𝑓⁡(𝑥) =(𝑥 +3)⁢(𝑥+1)2⁢(𝑥 −4) at each test value to determine if the function is positive or negative in that interval

Interval	Test 𝑥 in interval	𝑓 (test value)	> 0 or < 0?
𝑥 <−3	-4	72	> 0
−3 <𝑥 <−1	-2	-6	< 0
−1 <𝑥 <4	0	-12	< 0
𝑥 >4	5	288	> 0

On a number line this would look like:

From our test values, we can determine this function is positive when 𝑥 <−3 or 𝑥 >4, or in interval notation, (−∞,−3)⁢⋃(4,∞)

We could have also determined on which intervals the function was positive by sketching a graph of the function. We illustrate that technique in the next example

Example 4.4.6

Find the domain of the function 𝑣⁡(𝑡) =√6−5⁢𝑡−𝑡2.

Solution

A square root is only defined when the quantity we are taking the square root of, the quantity inside the square root, is zero or greater. Thus, the domain of this function will be when 6 −5⁢𝑡 −𝑡2 ≥0.

We start by solving the equality 6 −5⁢𝑡 −𝑡2 =0. While we could use the quadratic formula, this equation factors nicely to (6 +𝑡)⁢(1 −𝑡) =0, giving horizontal intercepts 𝑡 =1 and 𝑡 =−6.

Sketching a graph of this quadratic will allow us to determine when it is positive.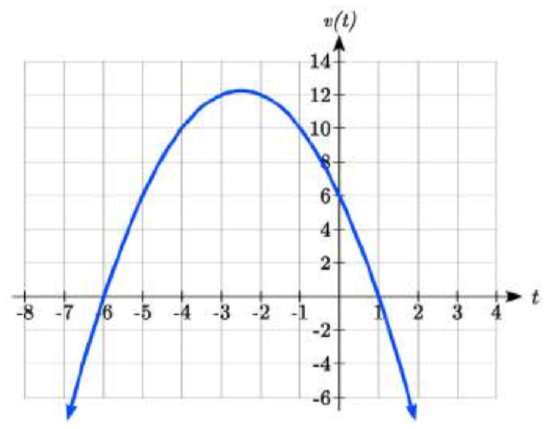

From the graph we can see this function is positive for inputs between the intercepts. So 6 −5⁢𝑡 −𝑡2 ≥0 for −6 ≤𝑡 ≤1, and this will be the domain of the 𝑣⁡(𝑡) function.

 

The Factor and Remainder Theorems

 

When we divide a polynomial, 𝑝⁡(𝑥) by some divisor polynomial 𝑑⁡(𝑥), we will get a quotient polynomial 𝑞⁡(𝑥) and possibly a remainder 𝑟⁡(𝑥). In other words,

𝑝⁡(𝑥)=𝑑⁡(𝑥)⁢𝑞⁡(𝑥)+𝑟⁡(𝑥)(4.4.1)

Because of the division, the remainder will either be zero, or a polynomial of lower degree than d(x). Because of this, if we divide a polynomial by a term of the form 𝑥 −𝑐, then the remainder will be zero or a constant.

If 𝑝⁡(𝑥) =(𝑥 −𝑐)⁢𝑞⁡(𝑥) +𝑟, then 𝑝⁡(𝑐) =(𝑐 −𝑐)⁢𝑞⁡(𝑐) +𝑟 =0 +𝑟 =𝑟, which establishes the Remainder Theorem.

The Remainder Theorem

If 𝑝⁡(𝑥) is a polynomial of degree 1 or greater and c is a real number, then when p(x) is divided by 𝑥 −𝑐, the remainder is 𝑝⁡(𝑐).

If 𝑥 −𝑐 is a factor of the polynomial 𝑝, then 𝑝⁡(𝑥) =(𝑥 −𝑐)⁢𝑞⁡(𝑥) for some polynomial 𝑞. Then 𝑝⁡(𝑐) =(𝑐 −𝑐)⁢𝑞⁡(𝑐) =0, showing 𝑐 is a zero of the polynomial. This shouldn’t surprise us - we already knew that if the polynomial factors it reveals the roots.

If 𝑝⁡(𝑐) =0, then the remainder theorem tells us that if p is divided by 𝑥 −𝑐, then the remainder will be zero, which means 𝑥 −𝑐 is a factor of 𝑝.

the factor theorem

If 𝑝⁡(𝑥) is a nonzero polynomial, then the real number 𝑐 is a zero of 𝑝⁡(𝑥) if and only if 𝑥 −𝑐 is a factor of 𝑝⁡(𝑥).

Synthetic Division

Since dividing by 𝑥 −𝑐 is a way to check if a number is a zero of the polynomial, it would be nice to have a faster way to divide by 𝑥 −𝑐 than having to use long division every time. Happily, quicker ways have been discovered.

Let’s look back at the long division we did in Example 1 and try to streamline it. First, let’s change all the subtractions into additions by distributing through the negatives.

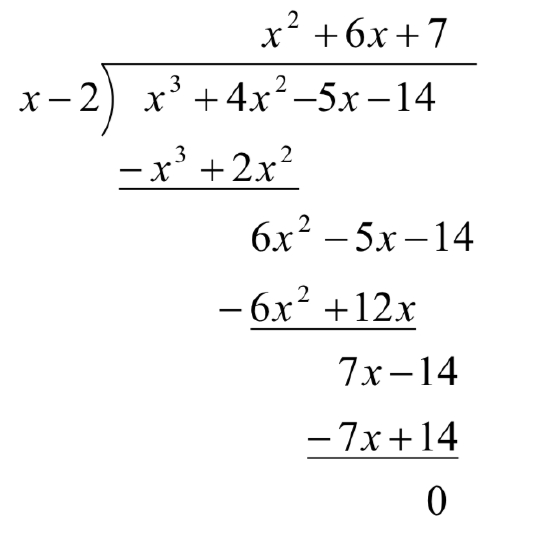
Next, observe that the terms −𝑥3, −6⁢𝑥2, and −7⁢𝑥 are the exact opposite of the terms above them. The algorithm we use ensures this is always the case, so we can omit them without losing any information. Also note that the terms we ‘bring down’ (namely the −5x and −14) aren’t really necessary to recopy, so we omit them, too.

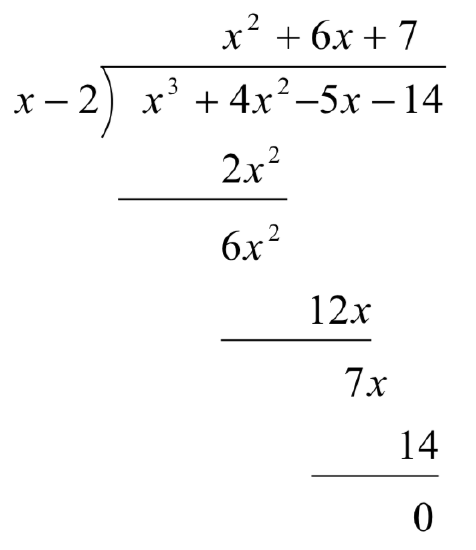
Now, let’s move things up a bit and, for reasons which will become clear in a moment, copy the 𝑥3 into the last row.

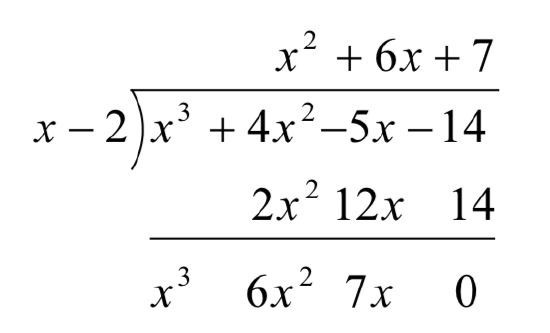
Note that by arranging things in this manner, each term in the last row is obtained by adding the two terms above it. Notice also that the quotient polynomial can be obtained by dividing each of the first three terms in the last row by 𝑥 and adding the results. If you take the time to work back through the original division problem, you will find that this is exactly the way we determined the quotient polynomial.

This means that we no longer need to write the quotient polynomial down, nor the 𝑥 in the divisor, to determine our answer.

 

 

 

 

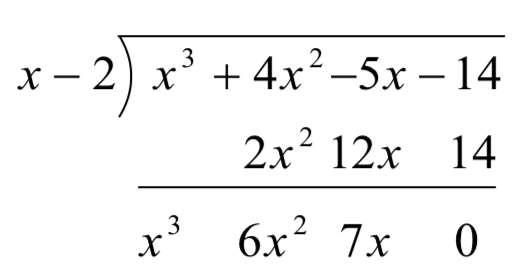
Important Topics of this Section

• Cauchy’s Bound for all real zeros of a polynomial
• Rational Roots Theorem
• Finding real zeros of a polynomial