14.10: Forced Oscillations and Resonance

Let us consider to the example of a mass on a spring. We now examine the case of forced oscillations, which we did not yet handle. That is, we consider the equation

$$mx'' + cx' + kx = F(t) \nonumber$$

for some nonzero $F(t)$. The setup is again: $m$ is mass, $c$ is friction, $k$ is the spring constant, and $F(t)$ is an external force acting on the mass.

Figure $\PageIndex{1}$

What we are interested in is periodic forcing, such as noncentered rotating parts, or perhaps loud sounds, or other sources of periodic force. Once we learn about Fourier series in Chapter 4, we will see that we cover all periodic functions by simply considering $F(t) = F_0 \cos (\omega t)$ (or sine instead of cosine, the calculations are essentially the same).

Below is a video on solving a forced oscillations problem.

Undamped Forced Motion and Resonance

First let us consider undamped $c = 0$ motion for simplicity. We have the equation

$$mx'' + kx = F_0 \cos (\omega t) \nonumber$$

This equation has the complementary solution (solution to the associated homogeneous equation)

$$x_c = C_1 \cos ( \omega_0t) + C_2 \sin (\omega_0t) \nonumber$$

where $\omega_0 = \sqrt { \frac {k}{m}}$ is the natural frequency (angular), which is the frequency at which the system “wants to oscillate” without external interference.

Let us suppose that $\omega_0 \neq \omega$. We try the solution $x_p = A \cos (\omega t)$ and solve for $A$. Note that we need not have sine in our trial solution as on the left hand side we will only get cosines anyway. If you include a sine it is fine; you will find that its coefficient will be zero.

We solve using the method of undetermined coefficients. We find that

$$x_p = \dfrac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber$$

We leave it as an exercise to do the algebra required.

The general solution is

$$x = C_1 \cos (\omega_0t) + C_2 \sin (\omega_0t) + \frac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber$$

or written another way

$$x = C \cos (\omega_0t - y ) + \frac {F_0}{m(\omega^2_0 - \omega^2)} \cos (\omega t) \nonumber$$

Hence it is a superposition of two cosine waves at different frequencies.

Example $\PageIndex{1}$

Take

$$0.5 x'' + 8 x = 10 \cos (\pi t), \quad x(0) = 0, \quad x' (0) = 0 \nonumber$$

Let us compute. First we read off the parameters: $\omega = \pi, \omega_0 = \sqrt { \frac {8}{0.5}} = 4, F_0 = 10, m = 0.5$. The general solution is

$$x = C_1 \cos (4t) + C_2 \sin (4t) + \frac {20}{16 - {\pi }^2} \cos ( \pi t) \nonumber$$

Solve for $C_1$ and $C_2$ using the initial conditions. It is easy to see that $C_1 = \frac {-20}{16 - {\pi}^2}$ and $C_2 = 0$. Hence

$$x = \frac {20}{16 - {\pi}^2} ( \cos (\pi t) - \cos ( 4t ) ) \nonumber$$

Figure $\PageIndex{2}$: Graph of $\frac {20}{16 - {\pi}^2} ( \cos ( \pi t) - \cos ( 4t ))$.

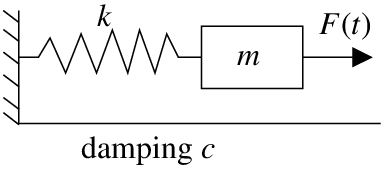
Notice the “beating” behavior in Figure $\PageIndex{2}$. First use the trigonometric identity

$$2 \sin ( \frac {A - B}{2}) \sin ( \frac {A + B}{2} ) = \cos B - \cos A \nonumber$$

to get that

$$x = \frac {20}{16 - {\pi}^2} ( 2 \sin ( \frac {4 - \pi}{2}t) \sin ( \frac {4 + \pi}{2} t)) \nonumber$$

Notice that $x$ is a high frequency wave modulated by a low frequency wave.

Now suppose that $\omega_0 = \omega$. Obviously, we cannot try the solution $A \cos (\omega t)$ and then use the method of undetermined coefficients. We notice that $\cos (\omega t)$ solves the associated homogeneous equation. Therefore, we need to try $x_p = At \cos (\omega t) + Bt \sin (\omega t)$. This time we do need the sine term since the second derivative of $t \cos (\omega t)$ does contain sines. We write the equation

$$x'' + \omega^2 x = \frac {F_0}{m} \cos (\omega t) \nonumber$$

Plugging $x_p$ into the left hand side we get

$$2B \omega \cos (\omega t) - 2A \omega \sin (\omega t) = \frac {F_0}{m} \cos (\omega t) \nonumber$$

Hence $A = 0$ and $B = \frac {F_0}{2m \omega }$. Our particular solution is $\frac {F_0}{2m \omega } t \sin (\omega t)$ and our general solution is

$$x = C_1 \cos (\omega t) + C_2 \sin (\omega t) + \frac {F_0}{2m \omega } t \sin (\omega t) \nonumber$$

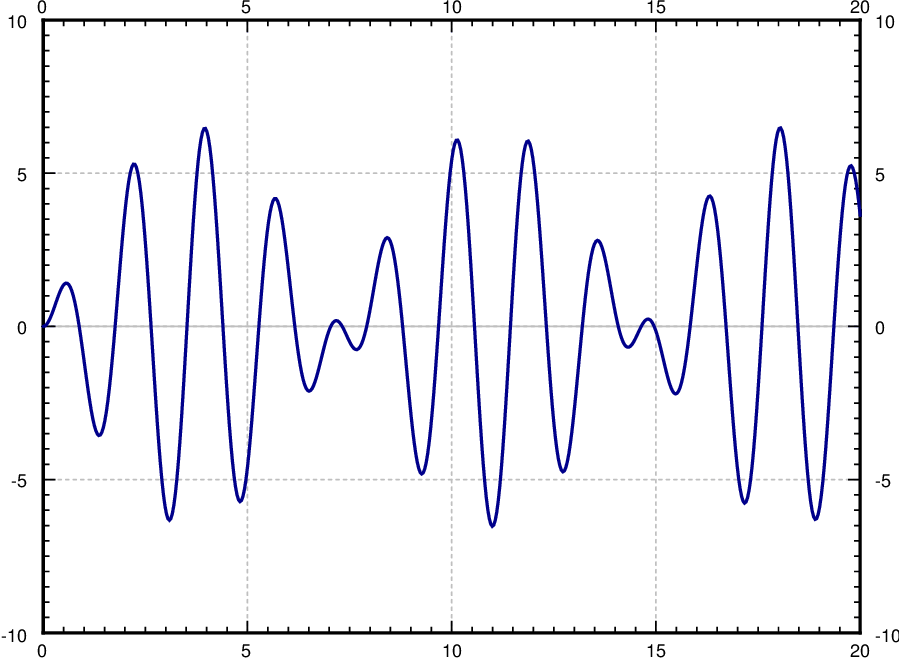
The important term is the last one (the particular solution we found). We can see that this term grows without bound as $t \rightarrow \infty$. In fact it oscillates between $\frac {F_0t}{2m \omega }$ and $\frac {-F_0t}{2m \omega }$. The first two terms only oscillate between $\pm \sqrt { C^2_1 + C^2_2}$, which becomes smaller and smaller in proportion to the oscillations of the last term as $t$ gets larger. In Figure $\PageIndex{3}$ we see the graph with $C_1 = C_2 = 0, F_0 = 2, m = 1, \omega = \pi$.

Figure $\PageIndex{3}$: Graph of $\frac{1}{\pi}t\sin (\pi t)$.

By forcing the system in just the right frequency we produce very wild oscillations. This kind of behavior is called resonance or perhaps pure resonance. Sometimes resonance is desired. For example, remember when as a kid you could start swinging by just moving back and forth on the swing seat in the “correct frequency”? You were trying to achieve resonance. The force of each one of your moves was small, but after a while it produced large swings.

On the other hand resonance can be destructive. In an earthquake some buildings collapse while others may be relatively undamaged. This is due to different buildings having different resonance frequencies. So figuring out the resonance frequency can be very important.

A common (but wrong) example of destructive force of resonance is the Tacoma Narrows bridge failure. It turns out there was a different phenomenon at play.$^{1}$

Below is a video on solving a differential equation that comes from a vibrating system with resonance.

Damped Forced Motion and Practical Resonance

In real life things are not as simple as they were above. There is, of course, some damping. Our equation becomes

$$\label{eq:15} mx'' + cx' + kx = F_0 \cos (\omega t),$$

for some $c > 0$. We have solved the homogeneous problem before. We let

$$p = \frac {c}{2m}\quad \omega_0 = \sqrt { \frac {k}{m} } \nonumber$$

We replace equation $\eqref{eq:15}$ with

$$x'' + 2px' + \omega^2_0x = \frac {F_0}{m} \cos (\omega t) \nonumber$$

The roots of the characteristic equation of the associated homogeneous problem are $r_1, r_2 = -p \pm \sqrt {p^2 - \omega_0^2}$. The form of the general solution of the associated homogeneous equation depends on the sign of $p^2 - \omega^2_0$, or equivalently on the sign of $c^2 - 4km$, as we have seen before. That is,

$$x_c = \begin {cases} C_1e^{r_1t} + C_2e^{r_2t}, & \text{if }c^2 > 4km, \\ C_1e^{pt} + C_2te^{-pt}, & \text{if }c^2 = 4km, \\ e^{-pt} ( C_1 \cos (\omega_1t) + C_2 \sin (\omega_1t)), & \text{if }c^2 < 4km, \end {cases} \nonumber$$

where $\omega_1 = \sqrt {\omega^2_0 - p^2 }$. In any case, we can see that $x_c(t) \rightarrow 0$ as $t \rightarrow \infty$. Furthermore, there can be no conflicts when trying to solve for the undetermined coefficients by trying $x_p = A \cos (\omega t) + B \sin (\omega t)$. Let us plug in and solve for $A$ and $B$. We get (the tedious details are left to reader)

$$((\omega^2_0 - \omega^2) B - 2 \omega pA ) \sin (\omega t) + ((\omega^2_0 - \omega^2) A + 2 \omega pB ) \cos (\omega t) = \frac {F_0}{m} \cos (\omega t) \nonumber$$

We get that

$$A = \frac { (\omega^2_0 - \omega^2) F_0}{m{(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \nonumber$$

$$B = \frac { 2 \omega pF_0}{m{(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \nonumber$$

We also compute $C = \sqrt { A^2 + B^2}$ to be

$$C = \frac {F_0}{m \sqrt { {(2 \omega p)}^2 + {(\omega^2_0 - \omega^2)}^2}} \nonumber$$

Thus our particular solution is

$$x_P = \frac {(\omega^2_0 - \omega^2)F_0}{m {(2 \omega p)}^2 + m {(\omega^2_0 - \omega^2)}^2} \cos (\omega t) + \frac {2 \omega pF_0}{m {(2 \omega p)}^2 + m{(\omega^2_0 - \omega^2)}^2} \sin (\omega t) \nonumber$$

Or in the alternative notation we have amplitude $C$ and phase shift $\gamma$ where (if $\omega \ne \omega_0$)

$$\tan \gamma = \frac {B}{A} = \frac {2 \omega p}{\omega^2_0 - \omega^2} \nonumber$$

Hence we have

$$x_p = \frac {F_0}{m \sqrt { {(2 \omega p)}^2 + {(\omega^2_0 - \omega ^2)}^2}} \cos (\omega t - \gamma) \nonumber$$

If $\omega = \omega_0$ we see that $A = 0, B = C = \frac {F_0}{2m \omega p}, ~\rm{and} ~ \gamma = \frac {\pi}{2}$.

The exact formula is not as important as the idea. Do not memorize the above formula, you should instead remember the ideas involved. For different forcing function $F$, you will get a different formula for $x_p$. So there is no point in memorizing this specific formula. You can always recompute it later or look it up if you really need it.

For reasons we will explain in a moment, we call $x_c$the transient solution and denote it by $x_{tr}$. We call the $x_p$ we found above the steady periodic solution and denote it by $x_{sp}$. The general solution to our problem is

$$x = x_c + x_p = x_{tr} + x_ {sp} \nonumber$$

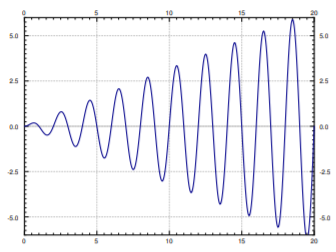
We note that $x_c = x_{tr}$ goes to zero as $t \rightarrow \infty$, as all the terms involve an exponential with a negative exponent. Hence for large $t$, the effect of $x_{tr}$ is negligible and we will essentially only see $x_{sp}$. Hence the name transient. Notice that $x_{sp}$ involves no arbitrary constants, and the initial conditions will only affect $x_{tr}$. This means that the effect of the initial conditions will be negligible after some period of time. Because of this behavior, we might as well focus on the steady periodic solution and ignore the transient solution. See Figure $\PageIndex{4}$ for a graph of different initial conditions.

Figure $\PageIndex{4}$: Solutions with different initial conditions for parameters $k = 1, m = 1, F_0 = 1, c = 0.7,$ and $\omega = 1.1.$

Notice that the speed at which $x_{tr}$ goes to zero depends on $P$ (and hence $c$). The bigger $P$ is (the bigger $c$ is), the “faster” $x_{tr}$ becomes negligible. So the smaller the damping, the longer the “transient region.” This agrees with the observation that when $c = 0$, the initial conditions affect the behavior for all time (i.e. an infinite “transient region”).

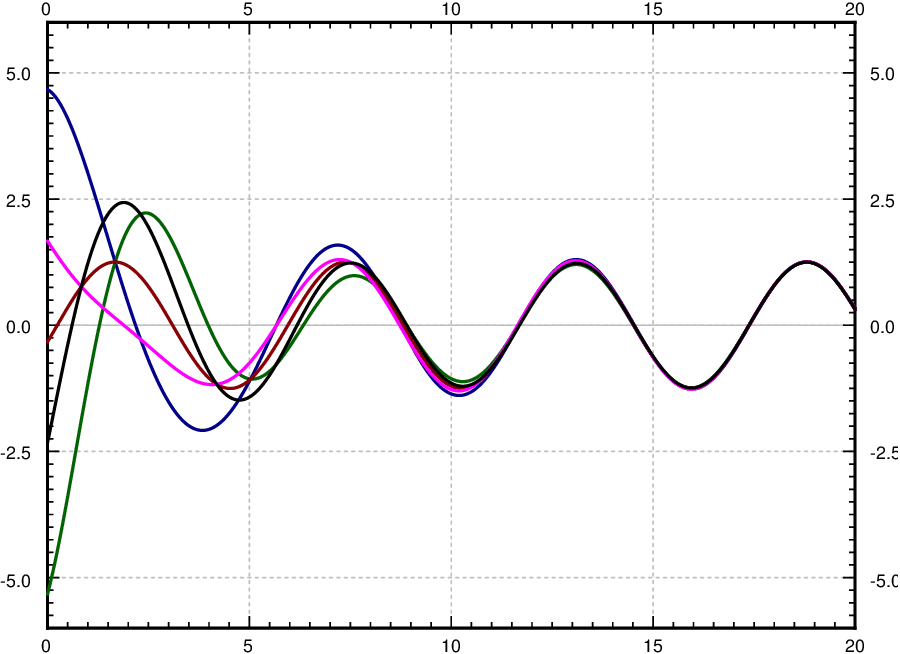
Let us describe what we mean by resonance when damping is present. Since there were no conflicts when solving with undetermined coefficient, there is no term that goes to infinity. What we will look at however is the maximum value of the amplitude of the steady periodic solution. Let $C$ be the amplitude of $x_{sp}$. If we plot $C$ as a function of $\omega$ (with all other parameters fixed) we can find its maximum. We call the $\omega$ that achieves this maximum the practical resonance frequency. We call the maximal amplitude $C(\omega )$ the practical resonance amplitude. Thus when damping is present we talk of practical resonance rather than pure resonance. A sample plot for three different values of $c$ is given in Figure $\PageIndex{5}$. As you can see the practical resonance amplitude grows as damping gets smaller, and any practical resonance can disappear when damping is large.

Figure $\PageIndex{5}$: Graph of $C( \omega )$ showing practical resonance with parameters $k = 1, m =1, F_0 = 1$. The top line is with $c = 0.4$, the middle line with $c = 0.8$, and the bottom line with $c = 1.6$.

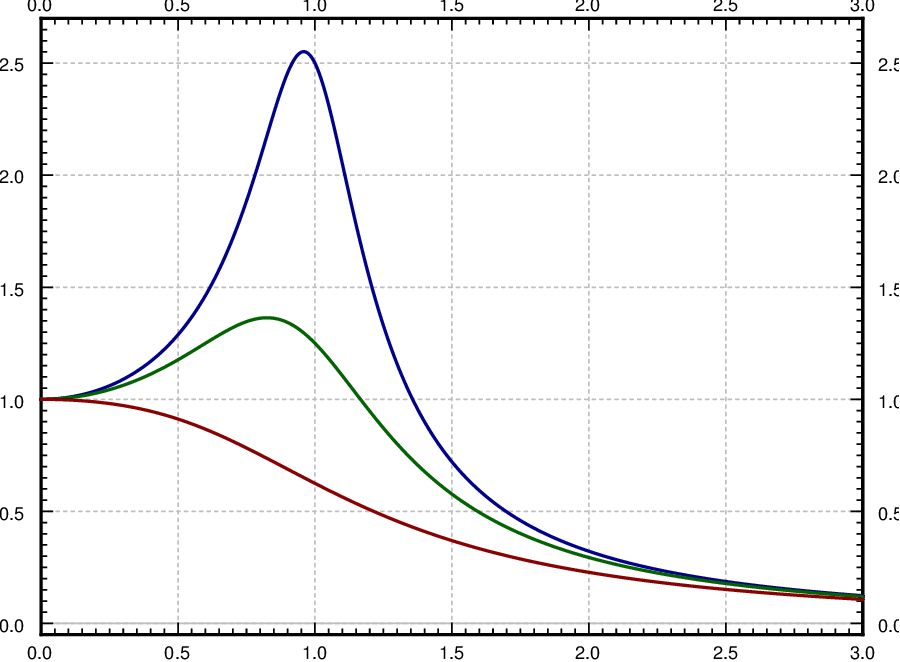
To find the maximum we need to find the derivative $C' (\omega )$. Computation shows

$$C' (\omega ) = \frac {-4 \omega (2p^2 + \omega^2 - \omega^2_0)F_0}{m {( {(2 \omega p)}^2 + {(\omega^2_0 - \omega^2)})}^{3/2}} \nonumber$$

This is zero either when $\omega = 0$ or when $2p^2 + \omega^2 - \omega^2_0 = 0$. In other words, $C' (\omega ) = 0$ when

$$\omega = \sqrt { \omega^2_0 - 2p^2} \rm{~or~} \omega = 0 \nonumber$$

It can be shown that if $\omega^2_0 - 2p^2$ is positive, then $\sqrt {\omega^2_0 - 2p^2}$ is the practical resonance frequency (that is the point where $C(\omega )$ is maximal, note that in this case $C' (\omega ) > 0$ for small $\omega$). If $\omega = 0$ is the maximum, then essentially there is no practical resonance since we assume that $\omega > 0$ in our system. In this case the amplitude gets larger as the forcing frequency gets smaller.

If practical resonance occurs, the frequency is smaller than $\omega_0$. As the damping $c$ (and hence $P$) becomes smaller, the practical resonance frequency goes to $\omega_0$. So when damping is very small, $\omega_0$ is a good estimate of the resonance frequency. This behavior agrees with the observation that when $c = 0$, then $\omega_0$ is the resonance frequency.

Another interesting observation to make is that when $\omega\to\infty$, then $\omega\to 0$. This means that if the forcing frequency gets too high it does not manage to get the mass moving in the mass-spring system. This is quite reasonable intuitively. If we wiggle back and forth really fast while sitting on a swing, we will not get it moving at all, no matter how forceful. Fast vibrations just cancel each other out before the mass has any chance of responding by moving one way or the other.

The behavior is more complicated if the forcing function is not an exact cosine wave, but for example a square wave. A general periodic function will be the sum (superposition) of many cosine waves of different frequencies. The reader is encouraged to come back to this section once we have learned about the Fourier series.

Footnotes

¹K. Billah and R. Scanlan, Resonance, Tacoma Narrows Bridge Failure, and Undergraduate Physics Textbooks, American Journal of Physics, 59(2), 1991, 118–124, http://www.ketchum.org/billah/Billah-Scanlan.pdf