2.5: Conversions

Last updated
Save as PDF

Page ID: 50934

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Many proportion problems can also be solved using dimensional analysis, the process of multiplying a quantity by rates to change the units. This process is also used in conversion problems.

Example $\PageIndex{1}$

Your car can drive 300 miles on a tank of 15 gallons. How far can it drive on 40 gallons?

Solution

We could certainly answer this question using a proportion: $\dfrac {300\text { miles}}{15\text { gallons}}= \dfrac {x\text { miles}}{40\text { gallons}}$

However, we earlier found that 300 miles on 15 gallons gives a rate of 20 miles per gallon. If we multiply the given 40 gallon quantity by this rate, the gallons unit “cancels” and we’re left with a number of miles:

\[40\text { gallons}\cdot \dfrac {20\text { miles}}{\text {gallon}} = \dfrac {40\text { gallons}}{1}\cdot \dfrac {20 \text { miles}}{\text {gallon}} = 800 \text { miles} \nonumber \]

If, instead, we were asked “how many gallons are needed to drive 50 miles?” we could answer this question by inverting the 20 mile per gallon rate so that the miles unit cancels and we’re left with gallons:

\[50 \text { miles} \cdot \dfrac {1 \text { gallon}}{20 \text { miles}} = \dfrac {50 \text { miles}}{1} \cdot \dfrac {1 \text { gallon}}{20 \text { miles}} = \dfrac {50 \text { gallons}}{20}=2.5 \text { gallons} \nonumber \]

Unit Conversions

Here are some unit conversions for reference.

For everyday use, you may want to download a free app for unit conversions.

Length

1 foot (ft) = 12 inches (in) 1 yard (yd) = 3 feet (ft)

1 mile = 5,280 feet

1000 millimeters (mm) = 1 meter (m) 100 centimeters (cm) = 1 meter

1000 meters (m) = 1 kilometer (km) 2.54 centimeters (cm) = 1 inch

Weight and Mass

1 pound (lb) = 16 ounces (oz) 1 ton = 2000 pounds

1000 milligrams (mg) = 1 gram (g) 1000 grams = 1kilogram (kg)

1 kilogram = 2.2 pounds (on earth)

Capacity (Volume)

1 cup = 8 fluid ounces (fl oz)* 1 pint = 2 cups

1 quart = 2 pints = 4 cups 1 gallon = 4 quarts = 16 cups

1000 milliliters (ml) = 1 liter (L)

*Fluid ounces are a capacity (volume) measurement for liquids. 1 fluid ounce ≈ 1 ounce (weight) for water only.

Example $\PageIndex{2}$

A bicycle is traveling at 15 miles per hour. How many feet will it cover in 20 seconds?

Solution

To answer this question, we need to convert 20 seconds into feet. If we know the speed of the bicycle in feet per second, this question would be simpler. Since we don’t, we will need to do additional unit conversions. We will need to know that 5280 ft = 1 mile. We might start by converting the speed into feet per second.

\[15 \dfrac {\text { miles}}{\text {hr}} = \dfrac {15 \text { miles}}{1 \text { hr}} \cdot \dfrac {5280 \text { ft}}{1 \text { mile}} = 79,200 \dfrac {\text { ft}}{\text {hr}} = \dfrac {79,200 \text { ft}}{\text {hr}} \cdot \dfrac {1 \text { hr}}{60 \text { min}} \cdot \dfrac{1 \text { min}}{60 \text { sec}} = 22 \dfrac {\text {ft}}{\text {sec}} \nonumber \]

\[22 \dfrac {\text { ft}}{\text {sec}} \cdot 20 \text { sec} = 400 \text { ft} \nonumber \]

Try it Now 4

A 1000 foot spool of bare 12-gauge copper wire weighs 19.8 pounds. How much will 18 inches of the wire weigh, in ounces?

Notice that with the miles per gallon example, if we double the miles driven, we double the gas used. Likewise, with the map distance example, if the map distance doubles, the real-life distance doubles. This is a key feature of proportional relationships, and one we must confirm before assuming two things are related proportionally.

Example $\PageIndex{3}$

Suppose you’re tiling the floor of a 10 ft by 10 ft room, and find that 100 tiles will be needed. How many tiles will be needed to tile the floor of a 20 ft by 20 ft room?

Solution

In this case, while the width the room has doubled, the area has quadrupled. Since the number of tiles needed corresponds with the area of the floor, not the width, 400 tiles will be needed. We could find this using a proportion based on the areas of the rooms:

\[\dfrac{100 \text { tiles}}{100 \text { ft}^{2}}=\dfrac{n \text { tiles}}{400 \text { ft}^{2}} \nonumber \]

Other quantities just don’t scale proportionally at all.

Example $\PageIndex{4}$

Suppose a small company spends $1000 on an advertising campaign, and gains 100 new customers from it. How many new customers should they expect if they spend $10,000?

Solution

While it is tempting to say that they will gain 1000 new customers, it is likely that additional advertising will be less effective than the initial advertising. For example, if the company is a hot tub store, there are likely only a fixed number of people interested in buying a hot tub, so there might not even be 1000 people in the town who would be potential customers.

Sometimes when working with rates, proportions, and percents, the process can be made more challenging by the magnitude of the numbers involved. Sometimes, large numbers are just difficult to comprehend.

Example $\PageIndex{5}$

Compare the 2010 U.S. military budget of $683.7 billion to other quantities.

Solution

Here we have a very large number, about $683,700,000,000 written out. Of course, imagining a billion dollars is very difficult, so it can help to compare it to other quantities.

If that amount of money was used to pay the salaries of the 1.4 million Walmart employees in the U.S., each would earn over $488,000.

There are about 300 million people in the U.S. The military budget is about $2,200 per person.

If you were to put $683.7 billion in $100 bills, and count out 1 per second, it would take 216 years to finish counting it.

Example $\PageIndex{6}$

Compare the electricity consumption per capita in China to the rate in Japan.

Solution

To address this question, we will first need data. From the CIA¹ website we can find the electricity consumption in 2011 for China was 4,693,000,000,000 KWH (kilowatt-hours), or 4.693 trillion KWH, while the consumption for Japan was 859,700,000,000, or 859.7 billion KWH. To find the rate per capita (per person), we will also need the population of the two countries. From the World Bank², we can find the population of China is 1,344,130,000, or 1.344 billion, and the population of Japan is 127,817,277, or 127.8 million.

Computing the consumption per capita for each country:

China: $\dfrac{4,693,000,000,000 \text { KWH}}{1,344,130,000 \text { people }} \approx 3491.5 \text { KWH}$ per person

Japan: $\dfrac{859,700,000,000 \text{ KWH}}{127,817,277 \text{ people}} \approx 6726 \text { KWH}$ per person

While China uses more than 5 times the electricity of Japan overall, because the population of Japan is so much smaller, it turns out Japan uses almost twice the electricity per person compared to China.

Geometry

Geometric shapes, as well as area and volumes, can often be important in problem solving.

Example $\PageIndex{7}$

You are curious how tall a tree is but don’t have any way to climb it. Describe a method for determining the height.

Solution

There are several approaches we could take. We’ll use one based on triangles, which requires that it’s a sunny day. Suppose the tree is casting a shadow, say 15 ft long. I can then have a friend help me measure my own shadow. Suppose I am 6 ft tall and cast a 2 ft shadow. Since the triangle formed by the tree and its shadow has the same angles as the triangle formed by me and my shadow, these triangles are called similar triangles, and their sides will scale proportionally. In other words, the ratio of height to width will be the same in both triangles. Using this, we can find the height of the tree, which we’ll denote by $h$:

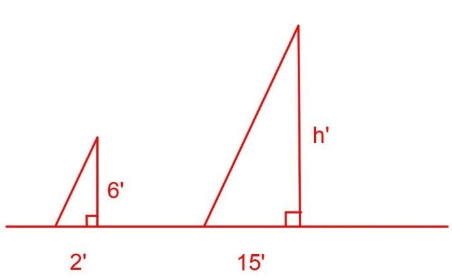
\[\dfrac{6 \text { ft tall}}{2 \text { ft shadow}}=\dfrac{h \text { ft tall}}{15 \text { ft shadow}} \nonumber \]

By cross multiplication, we get 2h=90. Thus, h=45(ft).

The tree is about 45 ft tall.

It may be helpful to recall some formulas for areas and volumes of a few basic shapes.

Areas

Rectangle

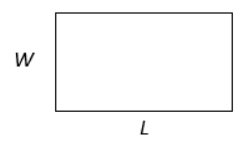
Area: $L \cdot W$

Perimeter: $2L + 2W $

Circle, radius $r$

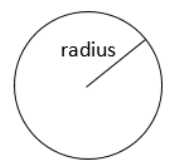
Area: $\pi r^2$

Circumference: $2\pi r$

Volumes

Rectangular Box

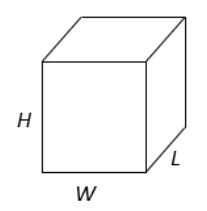
Volume: $L \cdot W \cdot H$

Cylinder

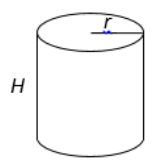
Volume: $\pi r^2 H$

Example $\PageIndex{8}$

If a 12 inch diameter pizza requires 10 ounces of dough, how much dough is needed for a 16 inch pizza?

Solution

To answer this question, we need to consider how the weight of the dough will scale. The weight will be based on the volume of the dough. However, since both pizzas will be about the same thickness, the weight will scale with the area of the top of the pizza. We can find the area of each pizza using the formula for area of a circle, $= \pi r^2$:

A 12” pizza has radius 6 inches, so the area will be $\pi 6^2$ = about 113 square inches.

A 16” pizza has radius 8 inches, so the area will be $\pi 6^2$ = about 201 square inches.

Notice that if both pizzas were 1 inch thick, the volumes would be 113 $\text {in}^3$ and 201 $\text {in}^3$ respectively, which are at the same ratio as the areas. As mentioned earlier, since the thickness is the same for both pizzas, we can safely ignore it.

We can now set up a proportion to find the weight of the dough for a 16” pizza:

\[\dfrac{10 \text { ounces }}{113 \text{in}^{2}}=\dfrac{x \text { ounces }}{201 \text{in}^{2}} \nonumber \]

Multiply both sides by 201.

$x=201 \cdot \dfrac{10}{113}=$ about 17.8 ounces of dough for a 16” pizza.

It is interesting to note that while the diameter is $\dfrac{16}{12}=1.33$ times as large, the dough required, which scales with area, is $1.33^2 = 1.78$ times as large.

Example $\PageIndex{9}$

A company makes regular and jumbo marshmallows. The regular marshmallow has 25 calories. How many calories will the jumbo marshmallow have?

Solution

We would expect the calories to scale with volume. Since the marshmallows have cylindrical shapes, we can use that formula to find the volume. From the grid in the image, we can estimate the radius and height of each marshmallow.

Figure $\PageIndex{6}$: Photo courtesy Christopher Danielson

The regular marshmallow appears to have a diameter of about 3.5 units, giving a radius of 1.75 units, and a height of about 3.5 units. The volume is about $\pi(1.75)^{2}(3.5)=33.7 \text { units }^{3}$.

The jumbo marshmallow appears to have a diameter of about 5.5 units, giving a radius of 2.75 units, and a height of about 5 units. The volume is about $\pi(2.75)^{2}(5)=118.8 \text { units }^{3}$.

We could now set up a proportion, or use rates. The regular marshmallow has 25 calories for 33.7 cubic units of volume. The jumbo marshmallow will have: $118.8 \text { units}^{3} \cdot \dfrac{25 \text { calories}}{33.7 \text { units }^{3}}=$88.1 \text { calories}$.

It is interesting to note that while the diameter and height are about 1.5 times as large for the jumbo marshmallow, the volume and calories are about $1.5^3 = 3.375$ times as large.

Try it Now 5

A website says that you’ll need 48 fifty-pound bags of sand to fill a sandbox that measure 8ft by 8ft by 1ft. How many bags would you need for a sandbox 6ft by 4ft by 1ft?

Reference

www.cia.gov/library/publicat.../2042rank.html
http://data.worldbank.org/indicator/SP.POP.TOTL

Contributors and Attributions

Saburo Matsumoto
CC-BY-4.0