9.2: How Big is Infinity? Or Is it “Infinities”?
- Page ID
- 50962
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The first numbers you learned as a child were probably whole numbers like 1, 2, 3, and so on. You learned basic quantitative facts like you have one nose, two ears, and ten fingers. So you learned to count before you learned how to add and subtract. You then grew up seeing a lot of objects like cars on the road, people in a concert, and stars in the sky and eventually learned, perhaps intuitively, that there is no end to this sequence of numbers {1, 2, 3, 4, 5, …}
In other words, you learned that there must be infinitely many numbers. But what exactly is infinity?
Whatever it is, it must be bigger than any number you can think of. And, in a sense, that’s not a bad definition. You may have seen the notation “∞" as the symbol for infinity; this symbol does NOT represent a number. That’s right. Let’s be clear: is not a number. We will come back to this notation later in this section.
Natural Numbers
The first set of numbers you learned, {1, 2, 3, 4, 5, …}, is called the set1 of natural numbers and is often denoted by the symbol \(\mathbb{N}\)2. Clearly, this set \(\mathbb{N}\) is an infinite set since it contains more than any finite number of objects, more than a billion, more than ten trillion, and so on. Now, you can easily see that the sum of any two natural numbers is also a natural number. Similarly, you can always take any two natural numbers and find the product, which is also a natural number. We call this property of \(\mathbb{N}\) “closure.” In other words, \(\mathbb{N}\) is “closed” under addition and multiplication.
But you have a problem when you try to subtract, say, 5 from 2. While both are natural numbers, the difference, 2 – 5, is not in \(\mathbb{N}\). We say, therefore, that \(\mathbb{N}\) is not closed under subtraction. For centuries, however, this did not cause any problem because this operation appeared to make no sense. After all, how can you take away five apples when you only have two? Or how can five people come out of a house which contains only two people?
Well, are there any applications for subtraction like 2 – 5? Of course there are. The temperature may go down by 5 degrees from 2 degrees (and the temperature just does not disappear). One can borrow $5 even though, for now, there may only be $2 in the account. So is there a way to make sense out of subtraction like this?
Integers
Of course, there is an easy way to fix this. Extend \(N\) to include numbers like 0, -1, -2, etc. We can then define a new set of numbers as follows:
\[\mathbb{Z}=\{0,\pm 1,\pm 2,\pm 3, \ldots\} \nonumber \]
Each of these numbers is called an integer. Of course, every natural number is an integer. So we now have two infinite sets, \(\mathbb{N}\) and \(\mathbb{Z}\). Obviously, \(\mathbb{Z}\) contains just about twice as many numbers as \(\mathbb{N}\), so perhaps \(\mathbb{Z}\) is “more infinite” than \(\mathbb{N}\), or are they both “just as infinite”? (This question itself sounds weird, doesn’t it?)
\(\mathbb{Z}\) is closed under addition, subtraction, and multiplication. This means that the sum, difference, and product of any two integers are all integers, members of \(\mathbb{Z}\). However, it is not closed under division because, for instance, 3 and 4 are both integers, but 3÷4 is not.
Rational Numbers
This gives rise to yet another infinite set, the set of fractions where both the numerator (top) and the denominator (bottom) are integers (and we assume that the denominator is not zero). This set, denoted with the symbol \(\mathbb{Q}\), is called the set of rational numbers (the term “rational” here comes from the word “ratio”). Any integer divided by any non-zero integer is a rational number—including all of the following:
\[\dfrac{1}{2}, \dfrac{-3}{5}, \dfrac{2}{-7}, \dfrac{-1}{-3}, \dfrac{5}{1}, \dfrac{-6}{2} \nonumber \]
Of course, the negative sign can be put on the top, bottom, or in the front of the fraction. Two negative signs cancel each other, and some of these fractions can be reduced. Note that every integer can be written with 1 in the denominator, so every integer is also a rational number. In other words, \(\mathbb{Q}\) is an infinite set which contains the entire set of integers (which contains the entire set of natural numbers). Thus, the size of the set \(\mathbb{Q}\) is bigger than the size of \(\mathbb{N}\) or \(\mathbb{Z}\), right? Or are they equally infinite?
An interesting (and perhaps confusing) property of rational numbers is that these numbers appear to show up “almost everywhere.” If you draw a number line (a straight line where each point represents a number), fractions appear almost everywhere while integers are “spread out” at an interval of 1.
For instance, between 0 and 1, there are no integers, but there are many fractions, i.e., rational numbers. As a matter of fact, between any two fractions, there are infinitely many fractions! Because of this property, we call \(\mathbb{Q}\) a “dense set.” Thus, certainly \(\mathbb{Q}\) appears to be a much, much larger set than the set of natural numbers or integers. But does this then mean that there are levels of infinity? Would it make sense to say that some infinite sets are bigger than other infinite sets?
The answer is mind-boggling (just as the question may be), but we are not quite there yet.
Before we get to the answer (and more questions), we will need at least one more infinite set. It is the set of real numbers, denoted \(\mathbb{R}\). Roughly speaking, a real number is a number represented by a point on the number line. For each point on the line, there is a real number, and vice-versa. Because each point on the line also represents the distance between that point and 0 (the origin), every real number can be thought of as the length of a line segment. Although a formal definition of a real number is quite difficult and is beyond the scope of this book, this idea of the number line gives us a good understanding of the set \(\mathbb{R}\), which is obviously infinite as it contains all of \(\mathbb{Q}\).
Irrational Numbers
Based on the paragraphs above, you may be under the impression that \(\mathbb{R}\) is the same set as \(\mathbb{Q}\), which seems to occupy virtually every point on the line already. Indeed, this was the thought of ancient Greek mathematicians before Pythagoras; they believed that every point on the line can be represented by a ratio of two integers. This idea went well with their philosophy that the world of beauty consists of ratios, and all they needed was ratios of integers, that is, \(\mathbb{Q}\). Pythagoras even used ratios and rational numbers to explain musical harmony and chords and is often referred to as the father of music theory (our modern notions like “perfect fifth” and “octave” in music are based on simple rational numbers). But it was also Pythagoras himself who proved that some real numbers (lengths) cannot be represented as a ratio of two integers. For example, imagine the right isosceles triangle (triangle with 45-, 45-, and 90-degree angles) where each of the two legs (the congruent sides) has length 1.
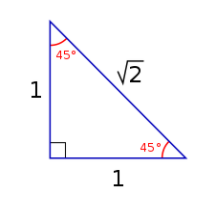
The hypotenuse, according to the theorem that bears Pythagoras’ name, has length 2. Pythagoras proved that no matter how hard one tries, it is impossible to represent 2 as the ratio of two integers, thus being forced to admit that there are real numbers (lengths of line segments) that are not rational numbers. These are now called irrational numbers. They include not only 2, 3, 5 and many other square roots, but also numbers like (the ratio between the circumference and the diameter of any circle) and e (the number we saw in the section on finance).
The set of real numbers, \(\mathbb{R}\), then contains both the set of rational numbers \(\mathbb{Q}\) and the set of irrational numbers, both on the number line, of course. Every point on the line is either a rational number or an irrational number. Once again, it is clear that \(\mathbb{R}\) contains the entire set \(\mathbb{Q}\) and much more.
Thus we now have four infinite sets, \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\), with each containing the previous set. Let us review:
\(\mathbb{N}=\{1,2,3,4, \ldots\}\): the set of natural numbers
\(\mathbb{Z}={0, \pm 1, \pm 2, \pm 3, \ldots }\): the set of integers
\(\mathbb{Q}=\left\{\dfrac{p}{q}\right\}\), where \(p\) and \(q\) are integers and \(q\) is not 0: the set of rational numbers
\(\mathbb{R}\), rational and irrational numbers: the set of real numbers
Georg Cantor and Set Theory
The idea of sets is so intuitive that mathematicians took it for granted for centuries. No one really paid much attention to this fundamental concept, at least formally, until Georg Cantor in the late 1800s. Cantor is one of the most interesting characters in the history of mathematics. He decided to take on the challenging problems involving infinity though many mathematicians had stayed away from infinity,
calling it as “belonging to the realm of the divine.” Obviously, everyone knew that there are many infinite sets, but Cantor came up with a way to compare their sizes. The size of a set \(S\) is called the cardinality of \(S\). For finite sets, the cardinality is simply the number of elements in that set. For instance, the set \(S=\{3,5,6,7\}\) and the set \(T=\{P, R, S, T\}\) both have four elements, so the cardinality of both of these sets is 4. For each finite natural number \(n\), there are sets with that cardinality (a simple example is the set \({1, 2, 3, …, n}\)). But how do you find the cardinality of an infinite set? If all of the infinite sets are of the same size, then there is just one infinite cardinality, and that would be the end of the story. However, as Cantor soon discovered, this was not the case.
The main tool Cantor used to measure and compare the sizes of various sets is “pairing.” In mathematics, this is called a one-to-one correspondence. It is a way to pair up elements of two different sets (say A and B) in such a way that every element of A is paired up with exactly one element of B with nothing left over on each side. For example, let’s say A is the set of five seats, labeled X1, X2, X3, X4, and X5, and B is the group of five people, Ann, Bob, Carl, Dee, and Ernie. If the five people sit in these seats, in the respective order, there is a natural pairing, or a one-to-one correspondence, in the following way:
Ann → X1
Bob → X2
Carl → X3
Dee → X4
Ernie → X5
No one is left standing, and every seat is occupied. When there is a one-to-one correspondence between two sets, you can clearly see that the two sets are of the same size (in this case, both A and B have the cardinality 5). Conversely, if two sets are of the same size, then there should be a one-to-one correspondence. Hence, we have the following:
Definition: Cardinality
Two sets have the same size (cardinality) if and only if there is a one-to-one correspondence between the two sets.
With a one-to-one correspondence, if you know the size of one set, you can determine the size of the other set without actually counting the elements. For instance, Dodger Stadium has 56,000 seats. If every person is sitting in one of these seats and if each seat is occupied by exactly one person, you know that there are exactly 56,000 seats in the stadium. So a one-to-one correspondence can be used to measure and compare the sizes of two sets.
This does not sound so hard, right? Well, that’s true between finite sets, but things can get a little tricky when infinite sets are involved. This is where Cantor made some ground-breaking discoveries at the end of the 19th century. Equipped with this definition, he found a way to define a one-to-one correspondence between \(\mathbb{N}\) and \(\mathbb{Z}\) even though, at a first glance, you may think \(\mathbb{N}\) is about half of \(\mathbb{Z}\) (because the natural numbers make up only the positive “half” of the integers). Here is one such one-to-one correspondence:
1 → 0, 2 → 1, 3 → – 1, 4 → 2, 5 → – 2, etc.
Note that the even numbers are paired up with positive numbers in \(\mathbb{Z}\) while the odd numbers are paired up with negative numbers in \(\mathbb{Z}\) without any duplication and with no elements of \(\mathbb{Z}\) left out.
Therefore, despite our intuition, \(\mathbb{N}\) and \(\mathbb{Z}\) have the same cardinality, i.e., they are “equally infinite,” or these two sets are of the same size. In fact, it is not difficult to see that all of the following proper subsets of \(\mathbb{N}\) are just “as big as” \(\mathbb{N}\) itself:
\(A_1=2, 4, 6, 8, 10, \dots \) (the set of positive natural numbers)
\(A_2=100, 200, 300, 400, \ldots \) (the set of positive multiples of 100)
\(A_3=2, 4, 8, 16, 32\ldots \) (the set of positive powers of 2)
This is strange because a part can be equal (in size) to the whole. In fact, \(A_2\) contains every 100th natural number (someone could say 1% of \(\mathbb{N}\)), but they are both equally infinite in the sense that their cardinalities are the same. This may lead one to believe that all infinite sets have the same cardinality and thus “equally big.”
But what about the dense set \(\mathbb{Q}\)? This set, the set of rational numbers, contains infinitely many fractions between any two real numbers (between any two distinct points on the line, there are infinitely many rational numbers). This must be much bigger than \(\mathbb{N}\) or \(\mathbb{Z}\), right?
Wrong!
Again, as counter-intuitive as it may be, Cantor proved that there is indeed a one-to-one correspondence between \(\mathbb{N}\) and \(\mathbb{Q}\), thus proving that these two sets are just “as infinite” as each other, i.e., they share the same cardinality. Yes, between 0 and 2, there is only one natural number, namely 1, while there are infinitely many rational numbers. In fact, there are infinitely many rational numbers between 0.999 and 1.001. Yet, the set of natural numbers is just as big as the set of rational numbers, and this fact has been mathematically verified.
You may not even be surprised that all of these sets are of the same size because, after all, they are all infinite, correct? Well, it turns out that is not true because here is another thing Cantor was able to show: \(\mathbb{R}\) is actually strictly bigger than \(\mathbb{N}\), \(\mathbb{Z}\) or \(\mathbb{Q}\). He prove this with an original, creative method called diagonalization. Essentially, he began by assuming that there is a one-to-one correspondence between \(\mathbb{N}\) and \(\mathbb{R}\) and then showed that this assumption would lead to a contradiction (because one can always come up with a real number left over after the pairing). Hence, we now know this truth:
Fact
The cardinality of \(\mathbb{R}\) is strictly bigger than the cardinality of \(\mathbb{N}\), \(\mathbb{Z}\) and \(\mathbb{Q}\). In other words, there are different levels of infinity.
Any cardinality that is not finite is called transfinite. Today, we denote the transfinite cardinality of \(\mathbb{N}\), \(\mathbb{Z}\), and \(\mathbb{Q}\) as 0(where is the first letter in the Hebrew alphabet and is pronounced ‘Aleph’). This is the first transfinite cardinality; in other words, you can say 0 is the “smallest infinity” though it may sound like an oxymoron and your friends and family may wonder if you are feeling okay. But wait. There is more.
It turns out that the cardinality of \(\mathbb{R}\) can be denoted as 20 (the number of subsets of \(\mathbb{N}\)), which, as stated above, is strictly bigger than 0. Furthermore, it was discovered that you can always take 2 to any aleph number (or any cardinality) to obtain a strictly bigger cardinality. By repeating this process indefinitely, one can obtain (wait for this…) infinite levels of infinite numbers. Here, then, is the conclusion:
Fact
There are infinitely many levels of infinities.
The story does not end here, either. Cantor also went on to prove many other theorems about transfinite cardinalities. At one point, after proving another surprising result, he famously wrote to his friend Dedekind, “I see it, but I don’t believe it.” Despite his outstanding contributions to mathematics, Cantor suffered from depression as his work on infinite cardinalities was often ridiculed and criticized. Even under those circumstances, however, he continued his work on mathematics. He introduced what has become known as the “Continuum Hypothesis,” which would (among many things) imply that there is no level of infinity between 0 and 20. This would mean that there are no sets strictly bigger than \(\mathbb{N}\) but strictly smaller than \(\mathbb{R}\). Is it true, or is it false? (It must be true or false, right?) Cantor actually made it his lifetime goal to prove this hypothesis and spent much of his energy in late years of his life trying to solve this problem. However, he passed away in 1918 in a mental institution without solving it. Little did he know then that a completely surprising ending would eventually put this fascinating problem to rest—but not for another 45 years. If you are interested in how this story ends (or in the life of Georg Cantor), you are encouraged to do a little research on the Internet or in the library to find out more.
Oh, one more thing… earlier the symbol was mentioned. This symbol is used to represent that which is bigger than any real number (on the real line); it does not represent any number. In particular, this symbol does not express any cardinality. It simply denotes the idea of “letting a real number x get bigger and bigger without bound.”
Challenging Exercises:
- Verify that each of the following numbers is rational. Then, use a calculator or a computer to express each as a decimal number. What do you notice about all of these decimal numbers?\[\dfrac{-2}{3} \quad \dfrac{3}{40} \quad \dfrac{2}{7} \quad \dfrac{12}{4} \quad-\dfrac{1}{32} \nonumber \]
- Classify the following numbers as natural numbers, integers, rational numbers, irrational numbers, or real numbers.\[
0.33 \quad 262 \quad -1 \dfrac{4}{5} \quad \dfrac{51}{3} \quad \dfrac{\pi}{2} \quad \quad -5 \quad 0 \quad 0.11111\ldots \nonumber \] - Try to pair up the elements of the two sets below to define a one-to-one correspondence. Describe your pairing so that each element is paired up with exactly one element and nothing is left behind.\[\begin{array}{c}
A=\{1,2,3,4,5, \ldots\} \\
B=\{4,8,12,16,20, \ldots\}
\end{array} \nonumber \] - Determine if each of the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\) is closed under addition and multiplication.
- It is mentioned in this section that \(\sqrt{2}, \pi \), and \(e\) are not rational. What other irrational numbers are there? Try to find ways to generate more irrational numbers (we know there are infinitely many of them).
Reference
- The term “set” is extremely difficult to define formally; here, we simply mean any collection of objects (like numbers).
- Some mathematicians, particularly those whose areas of expertise include set theory, include 0 as a natural number and simply call the set {1, 2, 3, 4, 5, …} the “set of positive integers.”
Contributors and Attributions
Saburo Matsumoto
CC-BY-4.0

