6.5: Area, Surface Area and Volume Formulas

Last updated
Save as PDF

Page ID: 51016

Amy Lagusker
College of the Canyons

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Area formulas

Let $b$ = base

Let $h$ = height

Let $s$ = side

Let $r$ = radius

Table 6.5.1: Area formulas
Shape Name	Shape	Area Formula
Rectangle	$clipboard_efe15c30b1007547b342fc746a7efcf20.png$	$A=bh$
Square	$clipboard_ec24caea3d5296d300e6f1f98eccae4d4.png$	$\begin{array}{l} A=b h \\ A=s^{2} \end{array}$
Parallelogram	$clipboard_eb485ee8fb60488e5bde456d41c01adeb.png$	$A=bh$
Triangle	$clipboard_e2212c051d12fc4634a8ee3f1eda28490.png$	$A=\dfrac{1}{2} b h$
Circle	$clipboard_e062a8ba2f01f7dbdd5050dc75b4afcfb.png$	$A=\pi r^{2}$
Trapezoid	$clipboard_e4f0ce691e022af3e89a66a7c366a6375.png$	$A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)$

Surface Area Formulas

Variables:

$SA$ = Surface Area

$B$ = area of the base of the figure

$P$ = perimeter of the base of the figure

$h$ = height

$s$ = slant height

$r$ = radius

Table 6.5.2: Surface Area formulas
Geometric Figure	Surface Area Formula	Surface Area Meaning
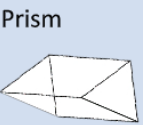
$clipboard_e81f9b4881086fecb9335c925c494c4e6.png$	$S A=2 B+P h$	Find the area of each face. Add up all areas.
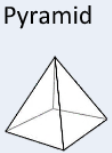
$clipboard_e917a9764b931cea8719511a37f526a89.png$	$S A=B+\dfrac{1}{2} s P$	Find the area of each face. Add up all areas.
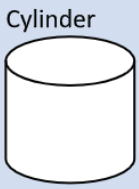
$clipboard_eaf05e34afb977462650d27c4706fb637.png$	$S A=2 B+2 \pi r h$	Find the area of the base, times 2, then add the areas to the areas of the rectangle, which is the circumference times the height.
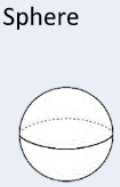
$clipboard_ea5d578ab0347abea37383a22a2492701.png$	$S A=4 \pi r^{2}$	Find the area of the great circle and multiply it by 4.
$clipboard_e9c547851612b12562b5185fe0605b0ad.png$	$S A=B+\pi r S$	Find the area of the base and add the product of the radius times the slant height times PI.

Volume Formulas

Variables:

$SA$ = Surface Area

$B$ = area of the base of the figure

$P$ = perimeter of the base of the figure

$h$ = height

$s$ = slant height

$r$ = radius

Table 6.5.3: Volume formulas
Geometric Figure	Volume Formula	Volume Meaning
$clipboard_e9a0de49a1375afc8775962a50a30a81b.png$	$V=B h$	Find the area of the base and multiply it by the height
$clipboard_e3a949ff5ec42fae21bd6c9a6773a69dc.png$	$V=\dfrac{1}{3} B h$	Find the area of the base and multiply it by 1/3 of the height.
$clipboard_e88f8e5771fdb263d07c69b2ddf933536.png$	$V=B h$	Find the area of the base and multiply it by the height.
$clipboard_e24e7962afe42ee50f4fc0758451cd560.png$	$V=\dfrac{4}{3} \pi r^{3}$	Find the area of the great circle and multiply it by the radius and then multiply it by 4/3.
$clipboard_ed295e65c6d76699d3776472f1c4b2c17.png$	$ V=\dfrac{1}{3} B h$	Find the area of the base and multiply it by 1/3 of the height.

Example $\PageIndex{1}$

Find the area of a circle with diameter of 14 feet.

Solution

\[\begin{aligned}A&=\pi r^{2}\\&=\pi(7)^{2}\\&=49 \pi \text {feet}^{2}\\&=153.86 \text {feet}^{2} \end{aligned} \nonumber \]

Example $\PageIndex{2}$

Find the area of a trapezoid with a height of 12 inches, and bases of 24 and 10 inches.

Solution

\[\begin{aligned} A&=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)\\ &=\dfrac{1}{2}(12)(24+10)\\ &=6(34)\\ &=204 \text { inches}^2 \end{aligned}\nonumber \]

Example $\PageIndex{3}$

Find the surface area of a cone with a slant height of 8 cm and a radius of 3 cm.

Solution

\[\begin{aligned}
SA&= B+\pi rS\\ &=\left(\pi r^{2}\right)+\pi rs\\ &=\left(\pi\left(3^{2}\right)\right)+\pi(3)(8) \\
&=9 \pi+24 \pi\\ &=33 \pi \text {cm}^{2}\\ &=103.62 \text {cm}^{2}
\end{aligned} \nonumber \]

Example $\PageIndex{4}$

Find the surface area of a rectangular pyramid with a slant height of 10 yards, a base width (b) of 8 yards and a base length (h) of 12 yards.

Solution

\[\begin{aligned}
SA&=B+\dfrac{1}{2} s P\\
&=(b h)+\dfrac{1}{2} s(2 b+2 h) \\
&=(8)(12)+\dfrac{1}{2}(10)(2(8)+2(12)) \\
&=96+\dfrac{1}{2}(10)(16+24) \\
&=96+5(40) \\
&=296 \text { yards}^{2}
\end{aligned} \nonumber \]

Example $\PageIndex{5}$

Find the volume of a sphere with a diameter of 6 meters.

Solution

\[\begin{aligned} V&=\dfrac{4}{3} \pi r^{3}\\ &=\dfrac{4}{3} \pi(3)^{3}\\ &=\dfrac{4}{3}(27 \pi)\\ &=36 \pi \text { meters }^{3}\\ &=113.04 \text { meters }^{3} \end{aligned} \nonumber \]

Partner Activity 1

Find the area of a triangle with a base of 40 inches and a height of 60 inches.
Find the area of a square with a side of 15 feet.
Find the surface area of Earth, which has a diameter of 7917.5 miles. Use 3.14 for PI.
Find the volume of a can a soup, which has a radius of 2 inches and a height of 3 inches. Use 3.14 for PI.

Practice Problems

(Problems 1 – 4) Find the area of each circle with the given parameters. Use 3.14 for PI. Round your answer to the nearest tenth.

Radius = 9 cm
Diameter = 6 miles
Radius = 8.6 cm
Diameter = 14 meters

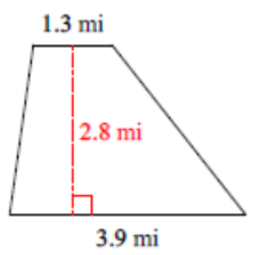
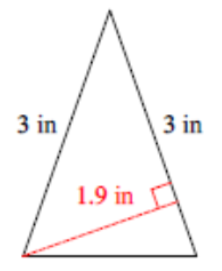
(Problems 5 – 8) Find the area of each polygon. Round answers to the nearest tenth.

$clipboard_e7c11d2a06b604c10f855daeef8996806.png$
$clipboard_e71f2d376b673e2eeedce58fde84d357b.png$
$clipboard_e2f13d1085ad717ca038c1450b452d3d1.png$
$clipboard_e1abd666b733c9eb5f7c9c6b081cdd56a.png$

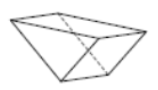
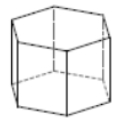
(Problems 9 – 12) Name each figure.

$clipboard_e9e2cc2664937ad831fbb674ad9999f14.png$
$clipboard_e0434f0d23c6a5e226b248f81e884b497.png$
$clipboard_e73a8e4539aa29805f2121f8d54380633.png$
$clipboard_e1b38ca5b795760abf9ea3f4ed234a5f3.png$

(Problems 13 – 17) Find the surface area of each figure. Leave your answers in terms of PI, if the answer contains PI. Round all other answers to the nearest hundredth.

$clipboard_e2209ea68bc005aa5e461f595277d41d9.png$
$clipboard_e6cc4dcb798c0d02022f26a2f8f7598c0.png$
$clipboard_e3a982ab4b0487b87494a4fc61271e4e0.png$
$clipboard_e4b6f66b4963ff0e17e58b75a7b6405ba.png$
$clipboard_e584c2ff25992a84eaa7e40796c297b23.png$

(Problems 18 – 25) Find the volume of each figure. Leave your answers in terms of PI, for answers that contain PI. Round all other answers to the nearest hundredth.

$clipboard_e0446db1e9293874d2e55a0a205226560.png$
$clipboard_eac0f896eb03b29a9f16544a127879fbd.png$
$clipboard_ee5baa989cb3bd5eb303b8cf115df882b.png$
$clipboard_e5b24dffcb97d63b1510c5f204e131818.png$
$clipboard_ebc8278c77a6141f1298d394b314e229e.png$
$clipboard_e6599552f2317bca580dc5b815ff3baf1.png$
$clipboard_ef7f0cda8e3c1436d52ef454dbff99d00.png$
$clipboard_ef61bb9b9104ce69d8becd339515a44e1.png$

Extension: Methods of Teaching Mathematics

Part 1

Assessments:

What is the Difference between Formative and Summative Assessments? Which One is More Important?
Formative Assessment Examples and When to Use Them
Summative Assessment Examples and When to Use Them

Part 2

Write a Formative and Summative Assessment for Your Lesson Plan

Part 3

Make sure you are working on Khan Academy throughout the semester.

Shape Name	Shape	Area Formula
Rectangle	$clipboard_efe15c30b1007547b342fc746a7efcf20.png$	\(A=bh\)
Square	$clipboard_ec24caea3d5296d300e6f1f98eccae4d4.png$	\(\begin{array}{l} A=b h \\ A=s^{2} \end{array}\)
Parallelogram	$clipboard_eb485ee8fb60488e5bde456d41c01adeb.png$	\(A=bh\)
Triangle	$clipboard_e2212c051d12fc4634a8ee3f1eda28490.png$	\(A=\dfrac{1}{2} b h\)
Circle	$clipboard_e062a8ba2f01f7dbdd5050dc75b4afcfb.png$	\(A=\pi r^{2}\)
Trapezoid	$clipboard_e4f0ce691e022af3e89a66a7c366a6375.png$	\(A=\dfrac{1}{2} h\left(b_{1}+b_{2}\right)\)

Geometric Figure	Surface Area Formula	Surface Area Meaning
$clipboard_e81f9b4881086fecb9335c925c494c4e6.png$	\(S A=2 B+P h\)	Find the area of each face. Add up all areas.
$clipboard_e917a9764b931cea8719511a37f526a89.png$	\(S A=B+\dfrac{1}{2} s P\)	Find the area of each face. Add up all areas.
$clipboard_eaf05e34afb977462650d27c4706fb637.png$	\(S A=2 B+2 \pi r h\)	Find the area of the base, times 2, then add the areas to the areas of the rectangle, which is the circumference times the height.
$clipboard_ea5d578ab0347abea37383a22a2492701.png$	\(S A=4 \pi r^{2}\)	Find the area of the great circle and multiply it by 4.
$clipboard_e9c547851612b12562b5185fe0605b0ad.png$	\(S A=B+\pi r S\)	Find the area of the base and add the product of the radius times the slant height times PI.

Geometric Figure	Volume Formula	Volume Meaning
$clipboard_e9a0de49a1375afc8775962a50a30a81b.png$	\(V=B h\)	Find the area of the base and multiply it by the height
$clipboard_e3a949ff5ec42fae21bd6c9a6773a69dc.png$	\(V=\dfrac{1}{3} B h\)	Find the area of the base and multiply it by 1/3 of the height.
$clipboard_e88f8e5771fdb263d07c69b2ddf933536.png$	\(V=B h\)	Find the area of the base and multiply it by the height.
$clipboard_e24e7962afe42ee50f4fc0758451cd560.png$	\(V=\dfrac{4}{3} \pi r^{3}\)	Find the area of the great circle and multiply it by the radius and then multiply it by 4/3.
$clipboard_ed295e65c6d76699d3776472f1c4b2c17.png$	\( V=\dfrac{1}{3} B h\)	Find the area of the base and multiply it by 1/3 of the height.